<目次>
(1) Kerasでロジスティクス回帰を実装した例をご紹介
(1-1) 実装のフローとポイント
(1-2) 実装例
(1) Kerasでロジスティクス回帰を実装した例をご紹介
ロジスティクス回帰を実装する際のポイント(実装のステップ)と、Kerasで実装したサンプルコードをご紹介します。
※ロジスティクス回帰とは?について知りたい方はこちらもご覧ください。
⇒(参考)ロジスティクス回帰とは?Excelで計算する方法もご紹介
(1-1) 実装のフローとポイント
●STEP1:モデルの定義
●STEP2:誤差関数の定義
●STEP3:最適化手法の定義(例:勾配降下法)
●STEP4:セッションの初期化
●STEP5:学習
(1-2) 実装例
############################################
# ロジスティック回帰(Keras版)
# 2022/XX/XX 初版作成
# 2022/08/10 X,tを関数の引数として外出し
#
# ※numpy未導入の場合「pip install numpy」を実行
# ※keras未導入の場合「pip install tensorflow」を実行
############################################
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD
# 入力層xの次元
M = 2
# 出力層yの次元(クラス数)
K = 1
# Epoc数の定義
epocs = 300
def or_gate(X_arg,t_arg):
############################################
# STEP1:モデルの定義
############################################
# 入力の電気信号xの初期化
X = X_arg
# 正解値tの定義
t = t_arg
# 入力層 - 出力層の定義
# Dense(input_dim=2, units=1):入力が2次元、出力が1次元のネットワーク
# ⇒ w1*x1 + w2+x2 + bに相当
# Activation('sigmoid'):活性化関数として、シグモイド関数を指定
# ⇒ y = σ(wx + b)に相当
model = Sequential([
Dense(input_dim=M, units=K),
Activation('sigmoid')
])
# 別の記述方法:add関数でも記述可能
#model = Sequential()
#model.add(Dense(input_dim=2, units=1))
#model.add(Activation('sigmoid'))
############################################
# STEP2:誤差関数の定義
############################################
# ⇒今回は不要
# (確率的勾配降下法の最終式を使うため、誤差関数Eは計算不要)
############################################
# STEP3:最適化手法の定義(例:確率的勾配降下法)
############################################
# loss='binary_crossentropy'
# 誤差関数の種類を指定。
# 2値(発火する/しない)の交差エントロピー関数の計算をさせる。
# SGD(lr=0.1)
# 最適化の手法を指定している。「SGD」は確率的勾配降下法で「lr」はその学習率。
# それぞれ「Stochastic Gradient Descent」と「learning rate」の頭文字を取っている。
model.compile(loss='binary_crossentropy',optimizer=SGD(lr=0.1))
############################################
# STEP4:セッションの初期化
############################################
# ⇒今回は不要
# (TensorFlow v2以降はSessionを使用しないため)
############################################
# STEP5:学習
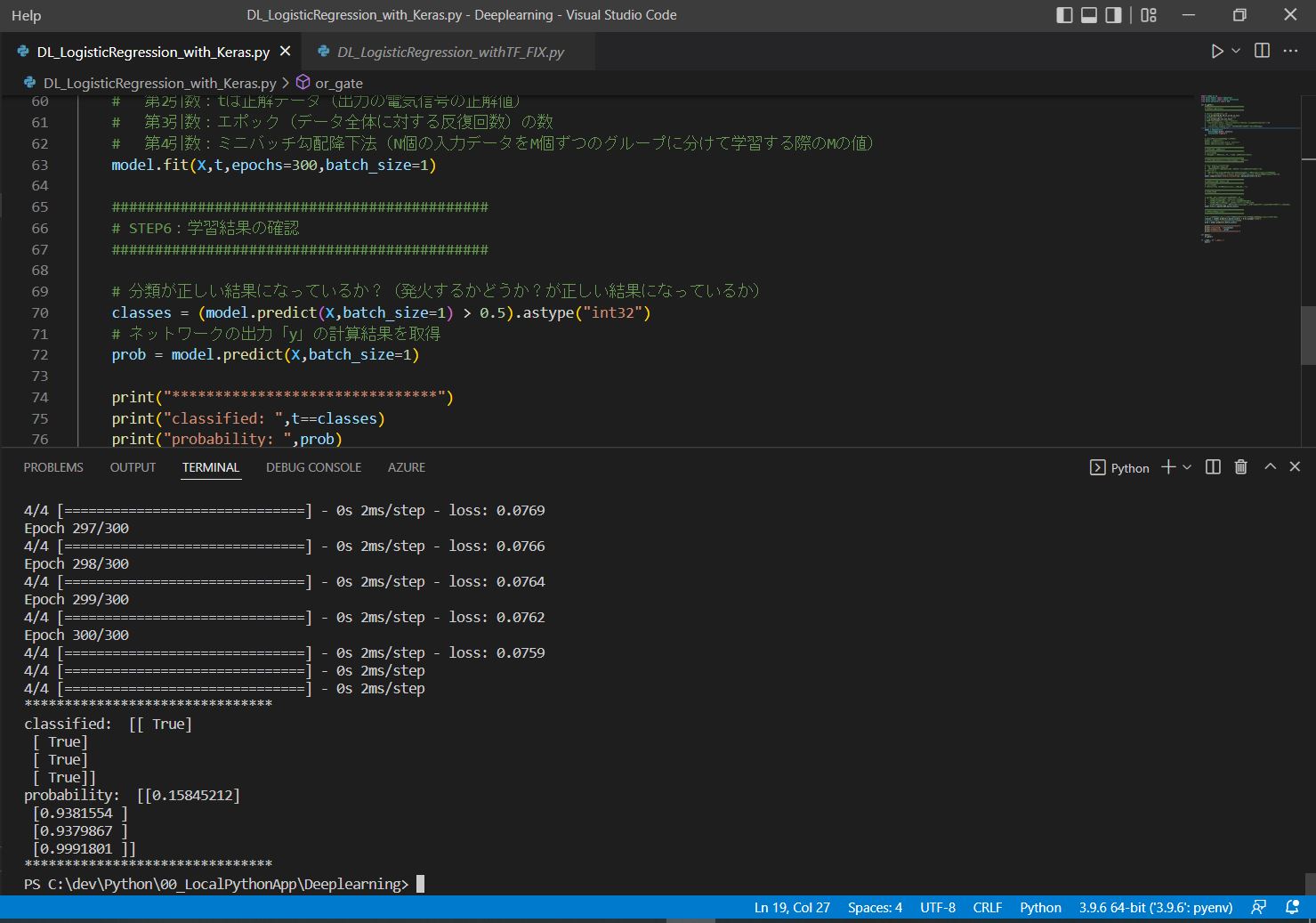
############################################
# 指定したエポック数、繰り返し学習を行う
# 第1引数:Xは入力データ(入力の電気信号)
# 第2引数:tは正解データ(出力の電気信号の正解値)
# 第3引数:エポック(データ全体に対する反復回数)の数
# 第4引数:ミニバッチ勾配降下法(N個の入力データをM個ずつのグループに分けて学習する際のMの値)
model.fit(X,t,epochs=epocs,batch_size=1)
############################################
# STEP6:学習結果の確認
############################################
# 分類が正しい結果になっているか?(発火するかどうか?が正しい結果になっているか)
classes = (model.predict(X,batch_size=1) > 0.5).astype("int32")
# ネットワークの出力「y」の計算結果を取得
prob = model.predict(X,batch_size=1)
print("===================",classes)
print("===================",t)
print("*******************************")
print("classified: ",t==classes)
print("probability: ",prob)
print("*******************************")
def main():
# 入力の電気信号xの初期化
X = np.array([[0,0],[0,1],[1,0],[1,1]])
# 正解値tの定義([0., 1., 1., 1.])
t = np.array([[0],[1],[1],[1]])
or_gate(X,t)
if __name__ == "__main__":
main()
Epoch 1/300 4/4 [==============================] - 0s 2ms/step - loss: 0.6296 Epoch 2/300 4/4 [==============================] - 0s 2ms/step - loss: 0.5790 ~中略~ Epoch 299/300 4/4 [==============================] - 0s 2ms/step - loss: 0.0762 Epoch 300/300 4/4 [==============================] - 0s 2ms/step - loss: 0.0759 ******************************* classified: [[ True] [ True] [ True] [ True]] probability: [[0.15845212] [0.9381554 ] [0.9379867 ] [0.9991801 ]] *******************************