(1) バイナリ―サーチとは?Javaのサンプルプログラムを用いて解説
(1-1) バイナリ―サーチのアルゴリズム
(1-2) バイナリ―サーチの性能(処理回数)
(1-3) バイナリ―サーチのサンプルプログラム
(1) バイナリ―サーチとは?Javaのサンプルプログラムを用いて解説
(1-1) バイナリ―サーチのアルゴリズム
(例)
上記処理の処理の流れを、次の配列で実際に確認します(テニス選手の名前です)。この配列はアルファベット順にソート済みです。
String[] name = {"Cilic","delPotro","Djokovic","Federer","Murray","Nadal","Nishikori","Thiem","Wawrinka","Zverev"};
この配列の中から錦織選手(Nishikori)を探す場合、探索範囲の下限(★lo)、上限(★hi)、中央(★mid)の動きはそれぞれ次のようになります。
(表)
| 配列インデックス | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 配列値 | Cilic | delPotro | Djokovic | Federer | Murray | Nadal | Nishikori | Thiem | Wawrinka | Zverev |
| 初期状態 | ★lo | o | o | o | ★mid | o | o | o | o | ★hi |
| 繰り返し1回目 | x | x | x | x | x | ★lo | o | ★mid | o | ★hi |
| 繰り返し2回目 | x | x | x | x | x | ★lo ★mid |
★hi | x | x | x |
| 繰り返し3回目 | x | x | x | x | x | x | ★hi ★lo ★mid |
x | x | x |
(表補足)
・「x」⇒midの更新処理により探索範囲外となった領域
・「o, ★lo, ★mid, ★hi」⇒現在対象となっている探索領域
(1-2) バイナリ―サーチの性能(処理回数)
バイナリーサーチは繰り返しの度に探索範囲が半分になります。上表でも、繰り返す毎に探索範囲のデータは10⇒5⇒2⇒1と半減していっています。
例えば256個のデータの場合は⓪256⇒①128⇒②64⇒③32⇒⑤16⇒⑥8⇒⑦4⇒⑧2⇒⑨1と8回の比較繰り返しが行われます。
これは次のようにlogの式で表現する事ができます。
$$ \log_2 256= 8 $$
つまり、N個のデータがある場合の比較回数は次のようになります。
$$ \log_2 N $$
>目次にもどる
(1-3) バイナリ―サーチのサンプルプログラム
(注意)
前提条件として探索対象の配列がキー情報でソートされていることが必要となります。
(サンプルプログラム)
public class IT0145_BinarySearch {
public static void main(String[] args) {
//探索対象の配列。探索するためにはここがソートされている必要あり。
String[] name = {"Cilic","delPotro","Djokovic","Federer","Murray","Nadal","Nishikori","Thiem","Wawrinka","Zverev"};
System.out.println("Serach Result : " + name[binarySearch(name,"Nishikori")] +" exists.");
}
static int binarySearch(String[] a, String key) {
//lo = 比較範囲の下限のインデックス(初期値は0)
int lo = 0;
//hi = 比較範囲の上限のインデックス(初期値はa.length-1)
int hi = a.length - 1;
while(lo <= hi) {
//midはloとhiの平均で求めます(※注1)
int mid = (lo + hi) / 2;
//求めたい値(key)と最新の中央値(mid)の大小関係をcompareToで比較します
int cmp = key.compareTo(a[mid]);
System.out.println("Lo="+lo+"("+a[lo]+")"+" Hi="+hi+"("+a[hi]+")"+" Mid="+mid+"("+a[mid]+")"+" cmp="+cmp);
//求めたい値(key) < 最新の中央値(mid)ならば
if (cmp < 0) {
//中央値(mid)より大きい部分には求めたい解は存在しないため
//hiの値を(mid - 1)で更新する(=探索範囲を半分に絞る)
hi = mid - 1;
}
//求めたい値(key) > 最新の中央値(mid)ならば
else if (cmp > 0) {
//中央値(mid)より小さい部分には求めたい解は存在しないため
//loの値を(mid + 1)で更新する(=探索範囲を半分に絞る)
lo = mid + 1;
}
//求めたい値(key) = 最新の中央値(mid)ならば
else {
//中央値=解のため、midを解として返す
return mid;
}
}
return lo;
}
}
(※注1)
下記の計算はintのオーバーフローを引き起こす可能性があるため、非常に大きな配列の探索を行うケースも見据えて「●改良後」の記述にする方が望ましいです。
●改良前
//midはloとhiの平均で求めます int mid = (lo + hi) / 2;
↓
●改良後
//midはloとhiの平均で求めます int mid = lo + (hi – lo) / 2;
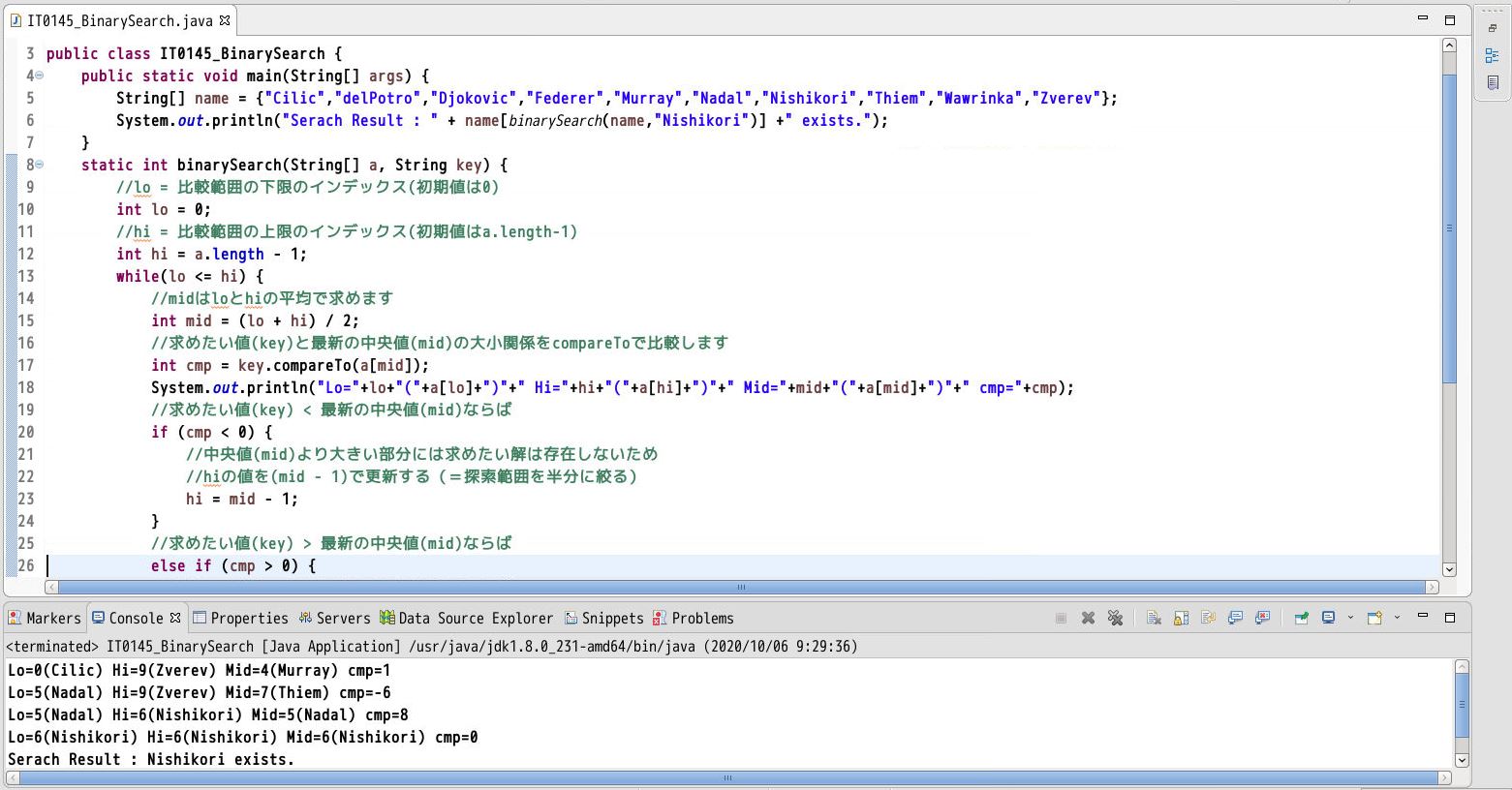
(実行結果)
上記プログラムをeclipse上で実行した結果を次に示します。
(図131)

お世話になります。
javaの勉強をしている最中で参考にさせて頂いております。
細かい点で恐縮ですが、以下の計算はオーバーフローしてしまう可能性があるのではと思いました。
――――――――――――――――――――――
//midはloとhiの平均で求めます
int mid = (lo + hi) / 2;
―――――――――――――――――――――――
lo + (hi – lo) / 2; の形が適切かと思いコメントをさせて頂きました。
もしかしたらわかりやすさ優先されているかもしれませんので
余計なお世話になりましたら申し訳ありません。
どうぞよろしくお願いいたします。
貴重なフィードバックを頂きありがとうございます。また確認およびご返信が遅れ申し訳ございませんでした。
本件、ご指摘頂いた通りです。
配列が非常に大きいケースで「lo + hi」がint型の最大を超えるケースでオーバーフローが発生する可能性があります。
補足事項として追記させて頂きました。
ありがとうございます。