ロジスティック回帰をエクセルで計算する方法（ディープラーニング）

＜目次＞

(１) ロジスティック回帰をエクセルで計算する方法（ディープラーニング）
　(１-１) 【前提①】ロジスティック回帰とは？
　(１-２) 【前提②】解決したい課題
　(１-３) ロジスティック回帰の流れを整理

(１) ロジスティック回帰をエクセルで計算する方法（ディープラーニング）

(１-１) 【前提①】ロジスティック回帰とは？

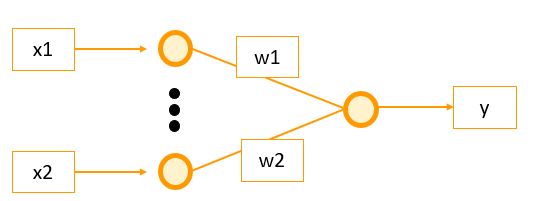
・ニューラルネットワークのモデルの種類の１つで、活性化関数として「シグモイド関数」を採用しているのが特徴です。

（図１００）イメージ図

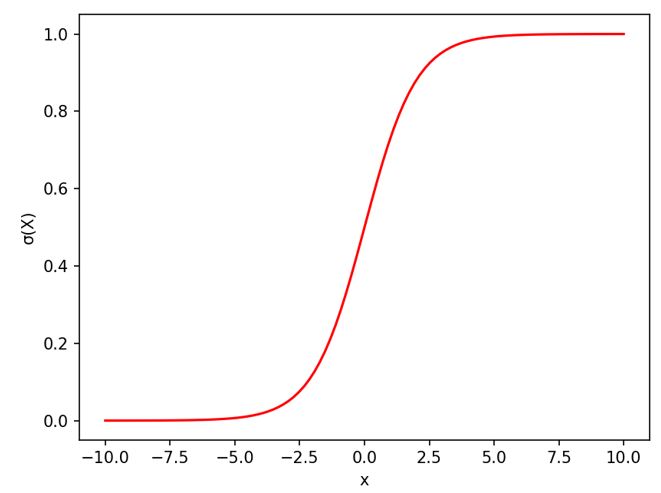
・シグモイド関数は0から1までの確率を表現できる関数なので、例えば「迷惑メールの振り分け処理」など微妙なラインでNG判定が出たものについては、受信トレイに一旦は通す、といったグレーゾーンのデータにも柔軟な対処が可能になります。

（式）シグモイド関数

$$ \sigma(x) = \frac{1}{1+e^{-x}}$$

＞目次にもどる

(１-２) 【前提②】解決したい課題

ロジスティック回帰は、バイナリ分類問題（つまり、2つのクラスにデータを分類する問題）を解くための統計的手法です。ロジスティック回帰では、入力された特徴の組み合わせから0から1の間の確率を出力します。この出力される確率を使って、閾値（例えば0.5）を基にしてデータを2つのクラスに分類します。

ロジスティック回帰の学習の際には、「ロジスティック損失関数」や「交差エントロピー損失関数」と呼ばれる特定の損失関数を最小化することを目指します。この損失関数を最小化するために、勾配降下法が使われます。

勾配降下法を使用して、ロジスティック損失関数の勾配（傾き）を計算し、この勾配情報を基にモデルのパラメータ（ロジスティック回帰の重みやバイアス）を更新します。この更新を繰り返すことで、最終的には損失関数が最小となるモデルのパラメータを見つけることができます。

＞目次にもどる

(１-３) ロジスティック回帰の流れを整理

(１-３-１) ●STEP1：分布の種類を仮定（シグモイド関数）【Excel】

今回はロジスティクス回帰なので活性化関数に「シグモイド関数」を使用

$ \sigma(x) = \frac{1}{1+e^{-x}} $

(１-３-２) ●STEP2：尤度関数を設定

・①確率密度関数

・ある入力電気信号「$\boldsymbol{x}$」に対して、ニューロンが発火する確率（確率変数C=1とする）

$ Pr(C=1|\boldsymbol{x})=\sigma(\boldsymbol{w}^\mathsf{T} \cdot \boldsymbol{x}+b) $

・ある入力電気信号「$\boldsymbol{x}$」に対して、ニューロンが発火しない確率（確率変数C=0とする）

$ Pr(C=0|\boldsymbol{x})=1-Pr(C=1|\boldsymbol{x}) $

・②確率密度関数の一般式

$y_n = \sigma(\boldsymbol{w}^\mathsf{T} \cdot \boldsymbol{x_n}+b)$と置くと、$t\in{0,1}$において一般式は次のように表せます。

$ Pr(C=t|\boldsymbol{x})=y^t (1-y)^{1-t} $

・③確率密度関数の一般式（別の表現）

これは表現を変えると、ある重み「$\boldsymbol{w}^\mathsf{T}$」とあるバイアス「$b$」の元で、入力電気信号が「$x$」になる確率とも表せます。

$ Pr(\boldsymbol{x}|\boldsymbol{w}^\mathsf{T},b)={y}^{t} (1-y)^{1-t} $

・④確率密度関数の一般式（入力N個の場合）

また、$N$個の入力データ$x_n (n=1,2,…)$と、それに対応する正解データ$t_n$が与えられた場合、確率は総乗として表現できる。

$ Pr(\boldsymbol{x_n}| \boldsymbol{w}^\mathsf{T},b) = \displaystyle \prod_{n=1}^N {y_n}^{t_n} (1-y_n)^{1-t_n} $

・⑤尤度関数

$ L(\boldsymbol{w},b| \boldsymbol{x_n})= \displaystyle \prod_{n=1}^N {y_n}^{t_n} (1-y_n)^{1-t_n} $

(１-３-３) ●STEP3：片方パラメータ（重みw）を固定して「バイアスb」を推定

(１-３-４) ●STEP4：片方パラメータ（重みw）を固定して「バイアスb」を推定

・①誤差関数（尤度関数の対数）【Excel】

$ E(\boldsymbol{w},b|\boldsymbol{x_n}) $

$ \quad= -\frac{1}{N} \log L(\boldsymbol{w},b|\boldsymbol{x_n}) $

$ \quad= -\frac{1}{N} \sum^{N}_{n=1} \lbrace {t_n}\log{y_n} + (1-t_n) \log (1-y_n) \rbrace $

・②勾配降下法

$ \boldsymbol{w}^{(k+1)} $

$ \quad=\boldsymbol{w}^{k}-\eta \frac{\partial E(\boldsymbol{w},b)}{\partial \boldsymbol{w}} $

$ \quad=\boldsymbol{w}^{k}-\eta \lbrace – \frac{1}{N} \sum^{N}_{n=1} (t_n-y_n) \boldsymbol{x_n} \rbrace $

$ \quad=\boldsymbol{w}^{k}+\eta \frac{1}{N} \sum^{N}_{n=1} (t_n-y_n) \boldsymbol{x_n} $

$ b^{(k+1)} $

$ \quad=b^{k}-\eta \frac{\partial E(\boldsymbol{w},b)}{\partial b} $

$ \quad=b^{k}-\eta \lbrace – \frac{1}{N} \sum^{N}_{n=1} (t_n-y_n) \rbrace $

$ \quad=b^{k}+\eta \frac{1}{N} \sum^{N}_{n=1} (t_n-y_n) $

・③確率的勾配降下法【Excel】

$ \boldsymbol{w}^{(k+1)} $

$ \quad=\boldsymbol{w}^{k}+\eta (t_n-y_n) \boldsymbol{x_n} $

$ b^{(k+1)} $

$ \quad=b^{k} +\eta (t_n-y_n) $

※「確率的勾配降下法」の詳細は別途「確率的勾配降下法（SGD）をロジスティック回帰に適用しPythonで実装した例をご紹介（★）」でご紹介していますので、ご興味あればご覧下さい。

(１-３-５) ●STEP5：尤度関数の最大値（＝傾き0＝偏微分が0）を求める【Excel】

→繰り返しにより求める

（参考）

尤度関数や最尤推定の考え方や内容を知りたい方は、下記記事も併せてご覧ください。

⇒参考①：最尤推定とは？考え方を実世界の例も交えシンプルにご紹介（★）

⇒参考②：確率と尤度の違いとは？概念や数式なども交えて比較紹介（★）

⇒参考③：最尤推定の計算を正規分布で行った例をご紹介（★）

＞目次にもどる

(１-４) ロジスティック回帰をExcelで計算

(１-４-１) ●STEP1：分布の種類を仮定（シグモイド関数）

・①活性化関数（シグモイド関数）【Excel】

[yn]=1/(1+EXP(-([xn1]*[w1]+[xn2]*[w2]+[b])))

(１-４-２) ●STEP3：片方パラメータ（重みw）を固定して「バイアスb」を推定

(１-４-３) ●STEP4：もう片方のパラメータ（バイアスb）を固定して「重みw」を推定

・①誤差関数（尤度関数の対数）【Excel】

[E]=(([t])*LN([y])+(1-[t])*LN(1-[y]))

・③確率的勾配降下法【Excel】

・重みw

[w1(k)] = [w1(k-1)] + [eta]*([tn]-[yn])*[xn1]
[w2(k)] = [w2(k-1)] + [eta]*([tn]-[yn])*[xn2]
・
・

→入力ニューロンの数分だけ計算

・バイアスb

[b(k)] = [b(k-1)] + [eta]*([tn]-[yn])

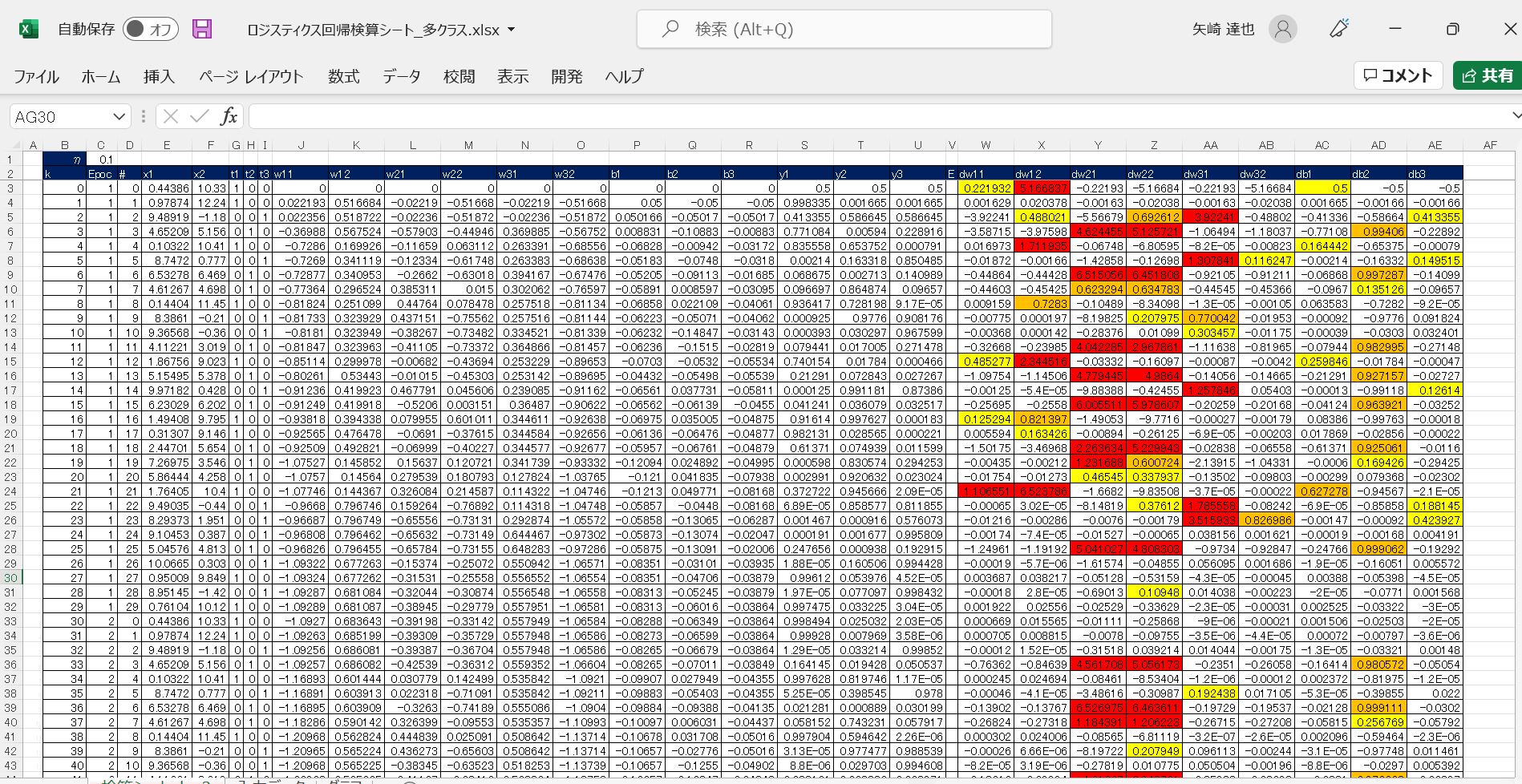
●ダウンロード用

→ロジスティクス回帰検算シート

（図１２１）

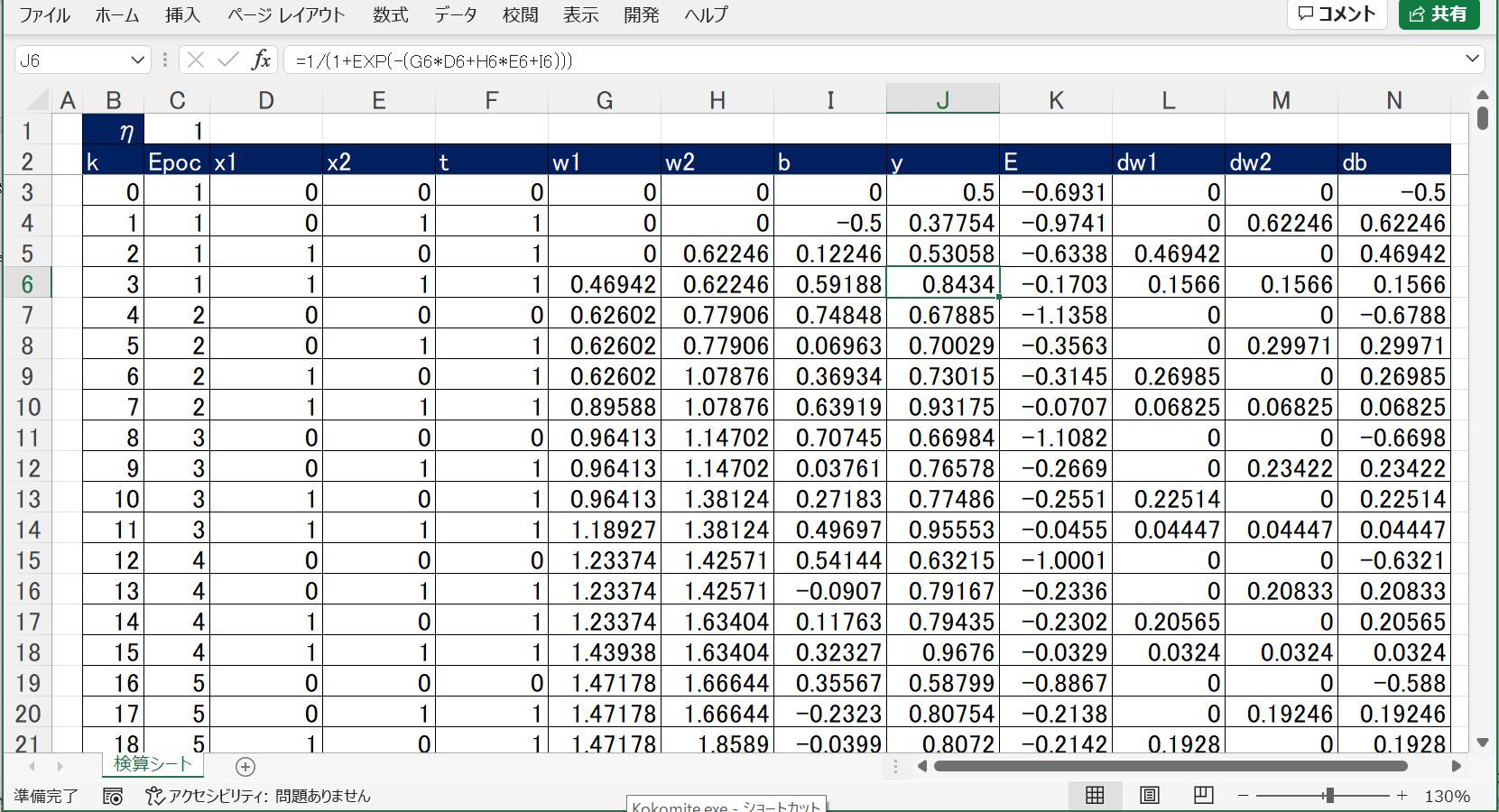
（注意点）

本来は繰り返し回数k毎にN個（例：4個）のデータからランダムに1個を選択する必要がありますが、今回は簡易的に1～Nの順番で取得しています（ランダムにはなっていない）。

＞目次にもどる