多層パーセプトロンをKerasで実装した例をご紹介

＜目次＞

多層パーセプトロンをKerasで実装した例をご紹介
　 (１-１) 実装のフローとポイント
　　 STEP1：モデルの定義
　　 STEP2：誤差関数の定義
　　 STEP3：最適化手法の定義（例：勾配降下法）
　　STEP4：セッションの初期化
　　 STEP5：学習
　 (１-２) 実装例

多層パーセプトロンをKerasで実装した例をご紹介

多クラスロジスティクス回帰を実装する際のポイント（実装のステップ）と、Kerasで実装したサンプルコードをご紹介します。

※多クラスロジスティクス回帰とは？について知りたい方はこちらもご覧ください。
⇒（参考）ロジスティック回帰の式変形（多クラス版）のご紹介（ディープラーニング）

(１-１) 実装のフローとポイント

●STEP1：モデルの定義

・入力の電気信号xの初期化
・正解値tの定義
・隠れ層（シグモイド）：h = softmax(Wx + b)の定義
・出力層（シグモイド）：y = softmax(Vh + c)の定義

（図111）

（補足①）
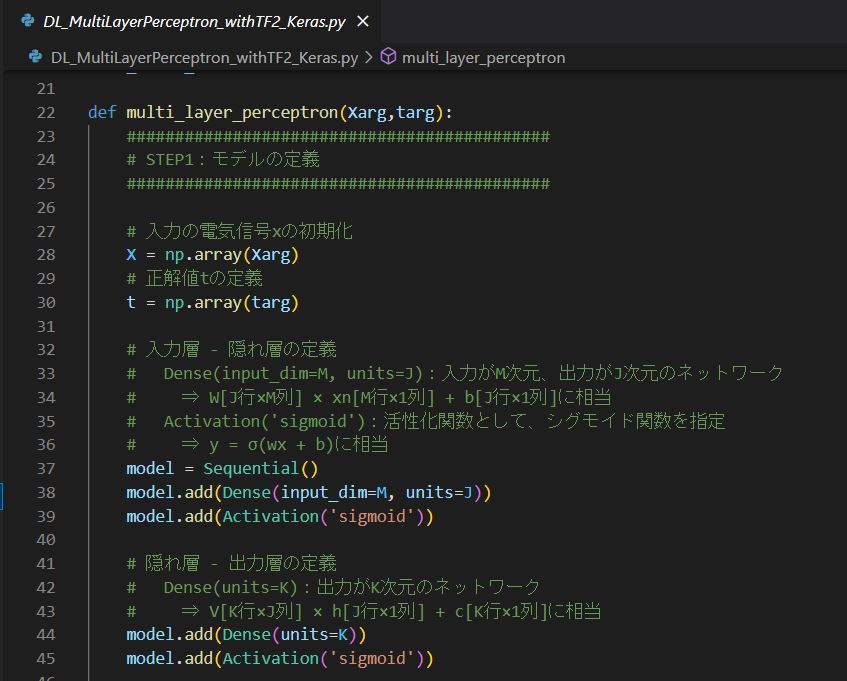
Kerasの場合、以下の項目は Sequentialクラスのインスタンス生成時に、引数で指定する Dense インスタンスや Activation インスタンスの中に内包されているため、単独の変数としては定義していない。

重みWの定義
バイアスbの定義
重みVの定義
バイアスcの定義

（図112）

（補足②）
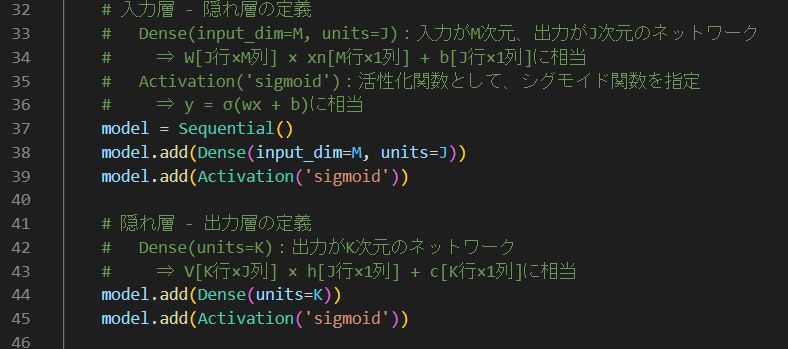
Kerasの場合、以下の項目は compile関数の中に内包されているため、単独の変数としては定義していない。

重みVの勾配（∂E(W,V,b,c)/∂V）の計算
バイアスcの勾配（∂E(W,V,b,c)/∂c）の計算
重みWの勾配（∂E(W,V,b,c)/∂W）の計算
バイアスbの勾配（∂E(W,V,b,c)/∂b）の計算
学習率：ηの定義

（図113）

●STEP2：誤差関数の定義

・交差エントロピー誤差関数：E(W,V,b,c) = -Σ[n=1…N] Σ[n=1…K]{tnk*log(ynk)}
⇒ 今回は不要（確率的勾配降下法を使うため、誤差関数Eは計算不要）

●STEP3：最適化手法の定義（例：勾配降下法）

Kerasの場合、最適化手法として確率的勾配降下法（SGD）を compile 関数で指定することにより、下記のような通常の実装で必要だった複雑な処理を明示的に記述する必要がなくなります。

（不要）Kerasでは明示的にこれらの処理を記述する必要なし：

隠れ層（シグモイド）：h = σ(Wx + b) の計算
出力層（シグモイド）：y = σ(Vh + c) の計算
重みVの勾配：∂E(W,V,b,c)/∂V の計算
バイアスcの勾配：∂E(W,V,b,c)/∂c の計算
重みWの勾配：∂E(W,V,b,c)/∂W の計算
バイアスbの勾配：∂E(W,V,b,c)/∂b の計算
重みV、Wの再計算
バイアスc、bの再計算

これらの処理は Keras に内包されているため、model.compile で最適化手法（SGD）と誤差関数を指定するだけで、自動的に計算されます。

●STEP4：セッションの初期化

今回は不要（TensorFlow v2以降はSessionを使用しないため）

●STEP5：学習

fit関数でエポックを指定して実行

＞目次にもどる

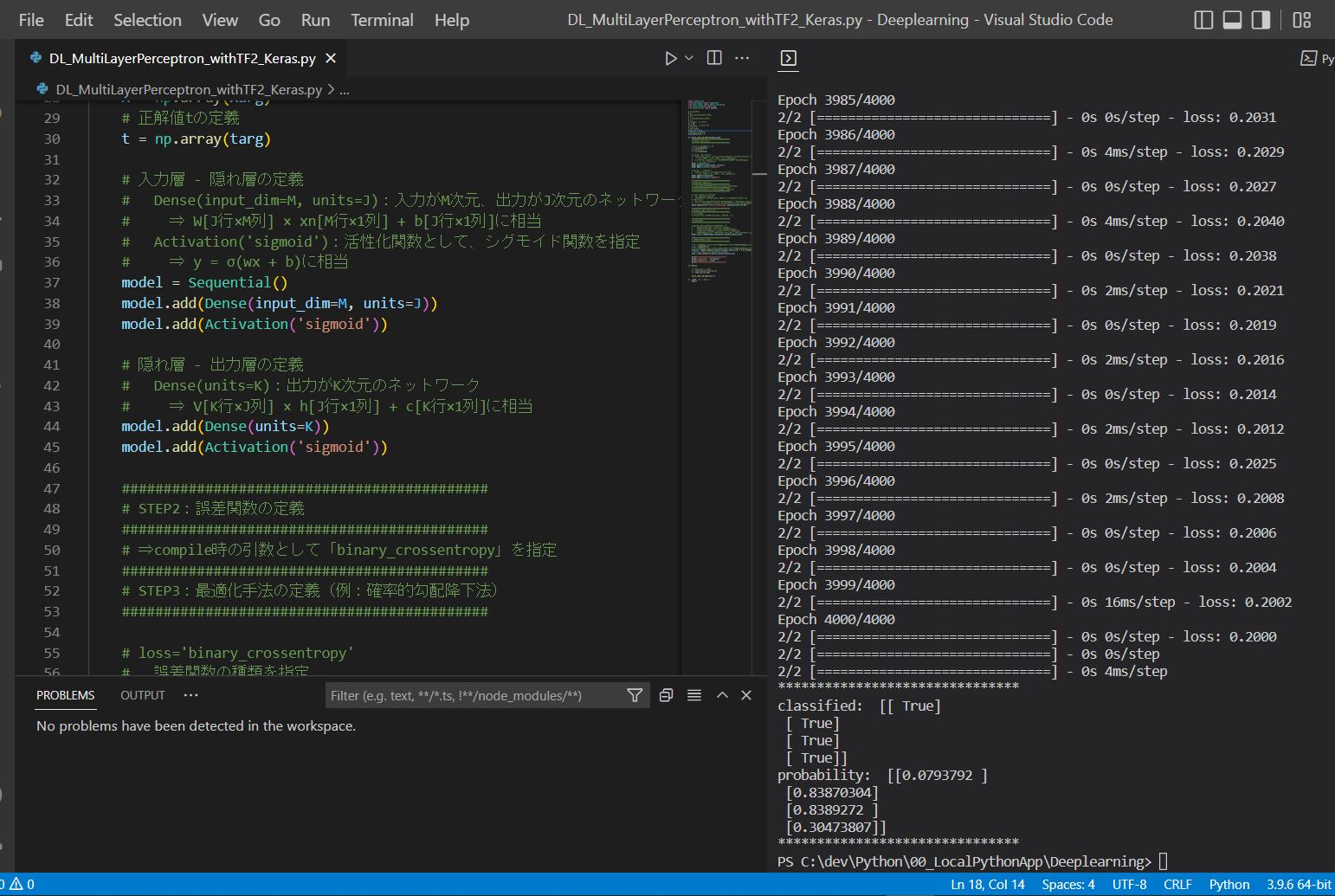
(１-２) 実装例

（サンプルプログラム）

import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD
from sklearn.utils import shuffle

# 入力xの次元
M = 2
# 隠れ層hの次元（クラス数）
J = 2
# 出力yの次元（クラス数）
K = 1
# 入力データセットの総
nc = 10
# 入力データセットの総数
N = nc * K
# エポック数
epoch_num = 2000
# ミニバッチのサイズ
mini_batch_size = 2

def multi_layer_perceptron(Xarg,targ):
    ############################################
    # STEP1：モデルの定義
    ############################################

    # 入力の電気信号xの初期化
    X = np.array(Xarg)
    # 正解値tの定義
    t = np.array(targ)

    # 入力層 - 隠れ層の定義
    # 　Dense(input_dim=M, units=J)：入力がM次元、出力がJ次元のネットワーク
    # 　　⇒ W[J行×M列] × xn[M行×1列] + b[J行×1列]に相当
    # 　Activation('sigmoid')：活性化関数として、シグモイド関数を指定
    # 　　⇒ y = σ(wx + b)に相当
    model = Sequential()
    model.add(Dense(input_dim=M, units=J))
    model.add(Activation('sigmoid'))
    
    # 隠れ層 - 出力層の定義
    # 　Dense(units=K)：出力がK次元のネットワーク
    # 　　⇒ V[K行×J列] × h[J行×1列] + c[K行×1列]に相当
    model.add(Dense(units=K))
    model.add(Activation('sigmoid'))

    ############################################
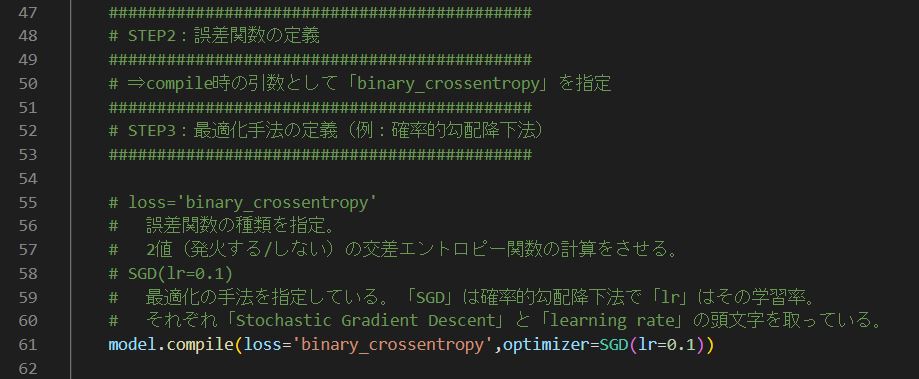
    # STEP2：誤差関数の定義
    ############################################
    # ⇒compile時の引数として「binary_crossentropy」を指定
    ############################################
    # STEP3：最適化手法の定義（例：確率的勾配降下法）
    ############################################

    # loss='binary_crossentropy'
    # 　誤差関数の種類を指定。
    # 　2値（発火する/しない）の交差エントロピー関数の計算をさせる。
    # SGD(lr=0.1)
    # 　最適化の手法を指定している。「SGD」は確率的勾配降下法で「lr」はその学習率。
    # 　それぞれ「Stochastic Gradient Descent」と「learning rate」の頭文字を取っている。
    model.compile(loss='binary_crossentropy',optimizer=SGD(lr=0.1))

    ############################################
    # STEP4：セッションの初期化
    ############################################
    # ⇒今回は不要
    # （TensorFlow v2以降はSessionを使用しないため）

    ############################################
    # STEP5：学習
    ############################################

    # 指定したエポック数、繰り返し学習を行う
    # 　第1引数：Xは入力データ（入力の電気信号）
    # 　第2引数：tは正解データ（出力の電気信号の正解値）
    # 　第3引数：エポック（データ全体に対する反復回数）の数
    # 　第4引数：ミニバッチ勾配降下法（N個の入力データをM個ずつのグループに分けて学習する際のMの値）
    model.fit(X,t,epochs=epoch_num,batch_size=mini_batch_size)

    ############################################
    # STEP6：学習結果の確認
    ############################################

    # 分類が正しい結果になっているか？（発火するかどうか？が正しい結果になっているか）
    X_,t_ = shuffle(X,t)
    # 分類が正しい結果になっているか？（発火するかどうか？が正しい結果になっているか）
    classes = (model.predict(X,batch_size=mini_batch_size) > 0.5).astype("int32")
    # ネットワークの出力「y」の計算結果を取得
    prob = model.predict(X,batch_size=mini_batch_size)

    print("*******************************")
    print("classified: ",t==classes)
    print("probability: ",prob)
    print("*******************************")

def main():

    # テスト用データセット
    X = [[0,0],[0,1],[1,0],[1,1]]
    t = [[0],[1],[1],[0]]

    multi_layer_perceptron(X,t)
  
if __name__ == "__main__":
    main()

実行結果（抜粋）

～中略～
Epoch 3997/4000
2/2 [==============================] - 0s 0s/step - loss: 0.2006
Epoch 3998/4000
2/2 [==============================] - 0s 0s/step - loss: 0.2004
...
*******************************
classified:  [[ True]
 [ True]
 [ True]
 [ True]]
probability:  [[0.0793792 ]
 [0.83870304]
 [0.8389272 ]
 [0.30473807]]
*******************************

（図121）

＞目次にもどる