<目次>
(1) ソフトマックス関数とは?ロジスティック回帰との関係性もご紹介
(1-1) 目的
(1-2) ソフトマックス関数とは?
(1-3) ソフトマックス関数の特徴
(1-4) ソフトマックス関数とロジスティック回帰の関係
(1-5) オマケ:Pythonでの計算
(1) ソフトマックス関数とは?ロジスティック回帰との関係性もご紹介
(1-1) 目的
ディープラーニングで頻繁に登場する「ソフトマックス関数」について、その特徴と「なぜニューラルネットワークで使われるのか?」を理解する。
>目次にもどる
(1-2) ソフトマックス関数とは?
ディープラーニングの分野において、ニューラルネットワークのモデルの出力層を定義する際の「活性化関数」などに利用される関数です。
・ソフトマックス関数の式
$$ softmax(x)_i = \frac{e^{x_i}}{\sum^{N}_{j=1}e_{x_j}} \quad (i=1,2,…,n) $$
・ソフトマックス関数の一般式
$$ \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix} = \frac{e^{x_i}}{\sum^{n}_{j=1}e_{x_j}} \begin{pmatrix} e_{x_1} \\ e_{x_2} \\ \vdots \\ e_{x_n} \end{pmatrix} $$
・総和が1になる
$$ \sum^{n}_{i=1} softmax(x)_i = 1 \quad (i=1,2,…,n) $$
(1-3) ソフトマックス関数の特徴
(図121)
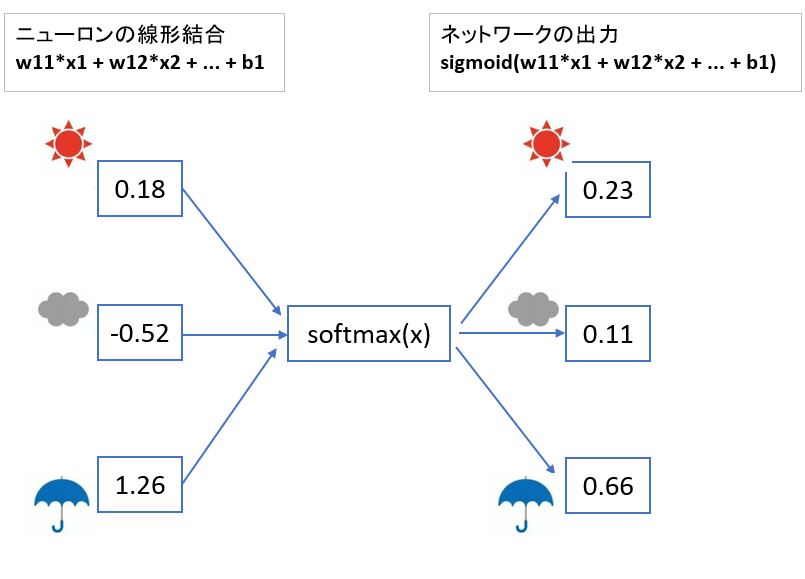
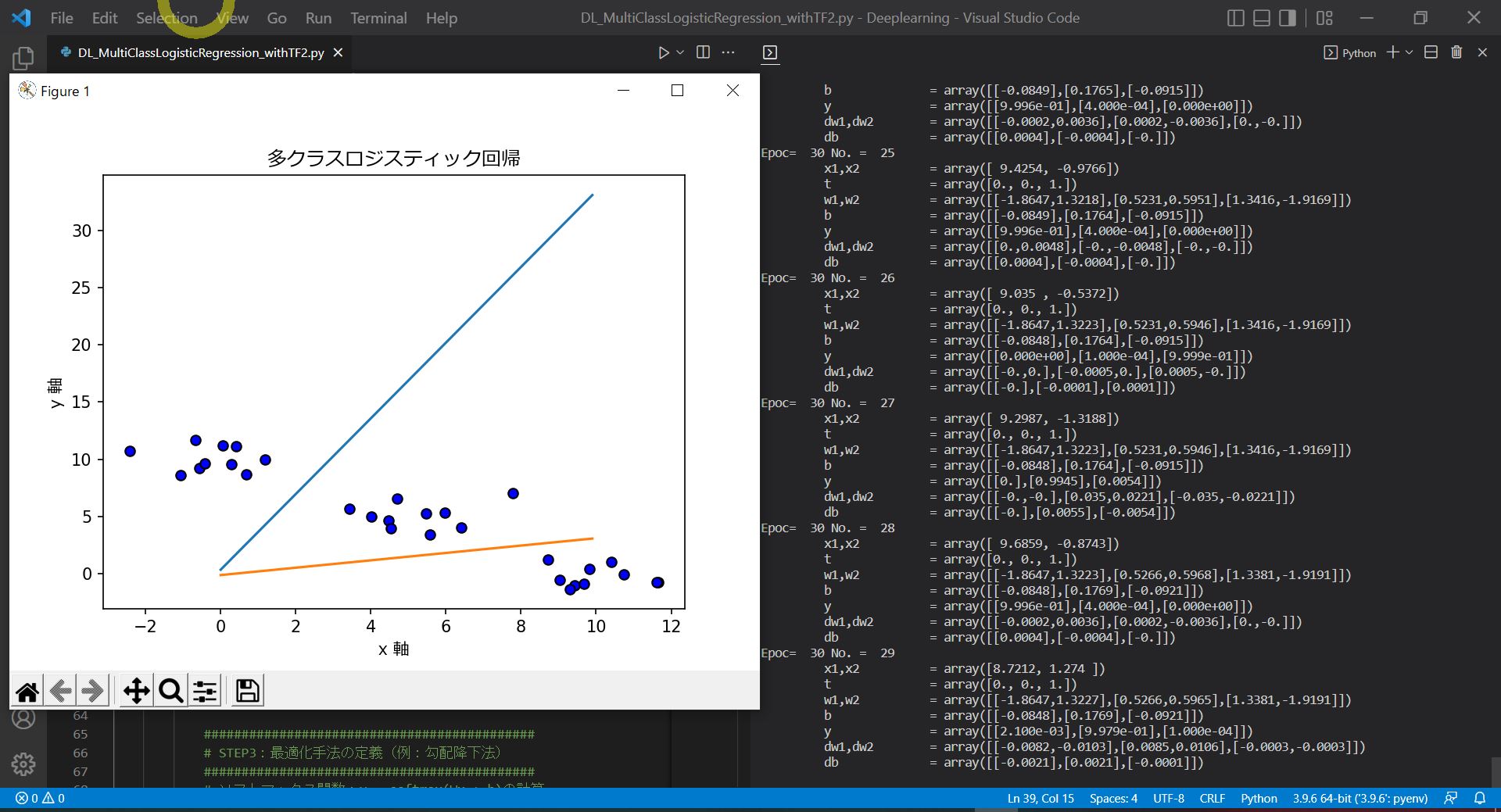
●特徴①:出力ynの元々の大小関係が保たれる
晴:0.18 → 0.23 (2番目に大きい)
曇:-0.52 → 0.11 (3番目に大きい)
雨:1.26 → 0.66 (1番目に大きい)
●特徴②:出力は0~1の範囲の数値になる
・変換前の出力が負の数でも、この法則は成り立ちます。
●特徴③:ベクトルの成分が正規化されている
・全部の出力(0.23 + 0.11 + 0.66)を足し合わせると1になる
$$ \sum^{n}_{i=1} softmax(x)_i = 1 \quad (i=1,2,…,n) $$
↓
上記の特徴を踏まえると、それぞれの事象が「相互に排他的」である限り、ソフトマックス関数の出力は「確率」として扱える。
>目次にもどる
(1-4) ソフトマックス関数とロジスティック回帰の関係
ソフトマックス関数は前述のような「特徴①~特徴③」を持っている事から、ニューラルネットワークのモデルとも非常に相性が良い事が分かっています。
・①ソフトマックス関数は「多クラスロジスティクス回帰」モデルの「活性化関数」として使われています。
⇒「活性化関数」は、ニューラルネットワークにおける出力(yの値)を決める関数です。
⇒つまり線形結合(x1*w1 +…+ xn*wn + b)後の出力yの決定に使う関数(ステップ関数、シグモイド関数)
・②ソフトマックス関数なら「多クラス分類」が可能
⇒ステップ関数やシグモイド関数は2値分類(発火する/しない)なので「迷惑メールである/でない」といった2値の分類しか出来ない。
⇒しかし、ソフトマックス関数なら「多クラス分類」が出来るので、例えば「晴れ/曇り/雨/雷/雪/台風」など2個以上の分類が可能
(図131)
(表1)
| ●モデル名 |
●活性化関数
⇒出力値を決定する関数 |
●出力クラス数 |
| 単純パーセプトロン |
ステップ関数 |
2
(2値分類)
⇒発火する/しないの2値のみ |
| ロジスティック回帰 |
シグモイド関数 |
2
(2値分類)
⇒発火する/しないの2値のみ |
| 多クラスロジスティック回帰 |
ソフトマックス関数 |
2以上
(多クラス分類) |
(参考)
・ステップ関数は2値(0か1)なので、グレーゾーンは表現できない
⇒(例)迷惑メールっぽいが、そうでないものも「迷惑メール判定」されてしまう
・シグモイド関数は「確率」を表現できるので、グレーゾーンも表現可能
⇒(例)迷惑メールっぽいが、そうでないものも「受信ボックス」に入れる判断も可能
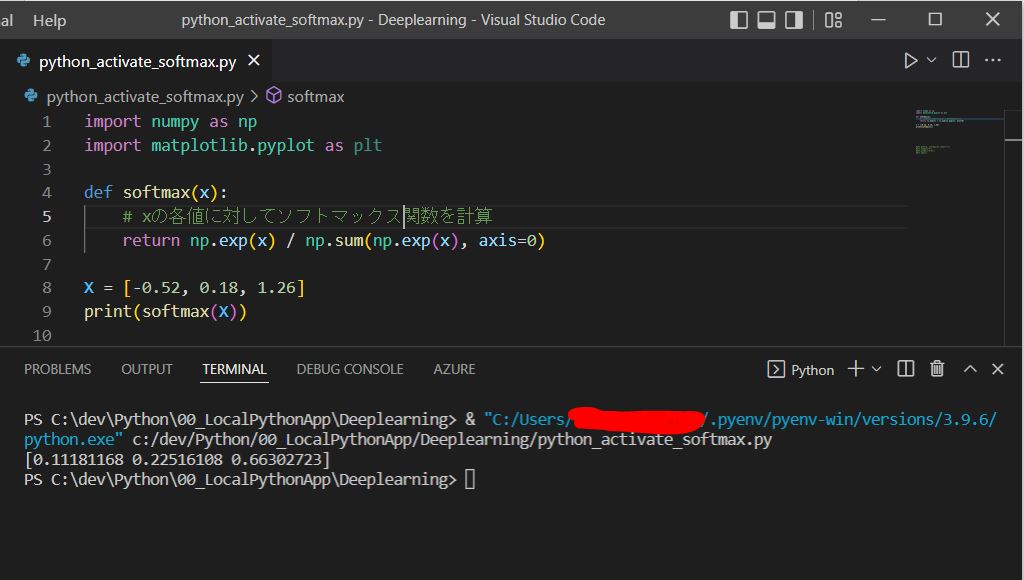
(1-5) オマケ:Pythonでの計算
(サンプル)
import numpy as np
import matplotlib.pyplot as plt
def softmax(x):
# xの各値に対してソフトマックス関数を計算
return np.exp(x) / np.sum(np.exp(x), axis=0)
X = [-0.52, 0.18, 1.26]
print(softmax(X))
(図141)
>目次にもどる