＜目次＞
勾配消失問題の対策（解決策）をご紹介（Kerasプログラムあり）
(１-１) 勾配消失問題とは？
(１-２) 勾配消失問題の対策方針
(１-３) 活性化関数による対策（tanh・ReLU）
勾配消失問題の対策（解決策）をご紹介（Kerasプログラムあり）
(１-１) 勾配消失問題とは？
勾配消失問題とは、ニューラルネットワークの学習において、誤差逆伝播の際に勾配が層を伝っていく中で徐々に小さくなり、最終的に学習が進まなくなる現象を指します。
→（参考）勾配消失問題とは？原因や対策についてもご紹介
(１-２) 勾配消失問題の対策方針
勾配消失の主な原因は、「微分すると値が小さくなる関数（例：シグモイド関数）」を用いている点にあります。そのため、対策としては「微分しても値が小さくなりにくい関数」を活性化関数として使うことが考えられます。ただし、出力層には「確率の関数」である必要があるため、シグモイド関数やソフトマックス関数を使うのが一般的です。一方、隠れ層に関しては、より勾配消失の影響を受けにくい活性化関数への変更が有効です。
Before（勾配消失が発生している例）
隠れ層にシグモイド関数を使用した場合の学習の様子です。
（図121）
Epoch 1/100 469/469 [==============================] - 2s 4ms/step - loss: 3.2976 - accuracy: 0.1034 Epoch 2/100 469/469 [==============================] - 2s 4ms/step - loss: 2.3066 - accuracy: 0.1049 ～中略～ Epoch 100/100 469/469 [==============================] - 2s 4ms/step - loss: 2.3097 - accuracy: 0.1040 313/313 [==============================] - 1s 2ms/step - loss: 2.3104 - accuracy: 0.1009 [2.3104090690612793, 0.10090000182390213]
(１-３) 活性化関数による対策（tanh・ReLU）
対策①：双曲線正接関数（tanh）
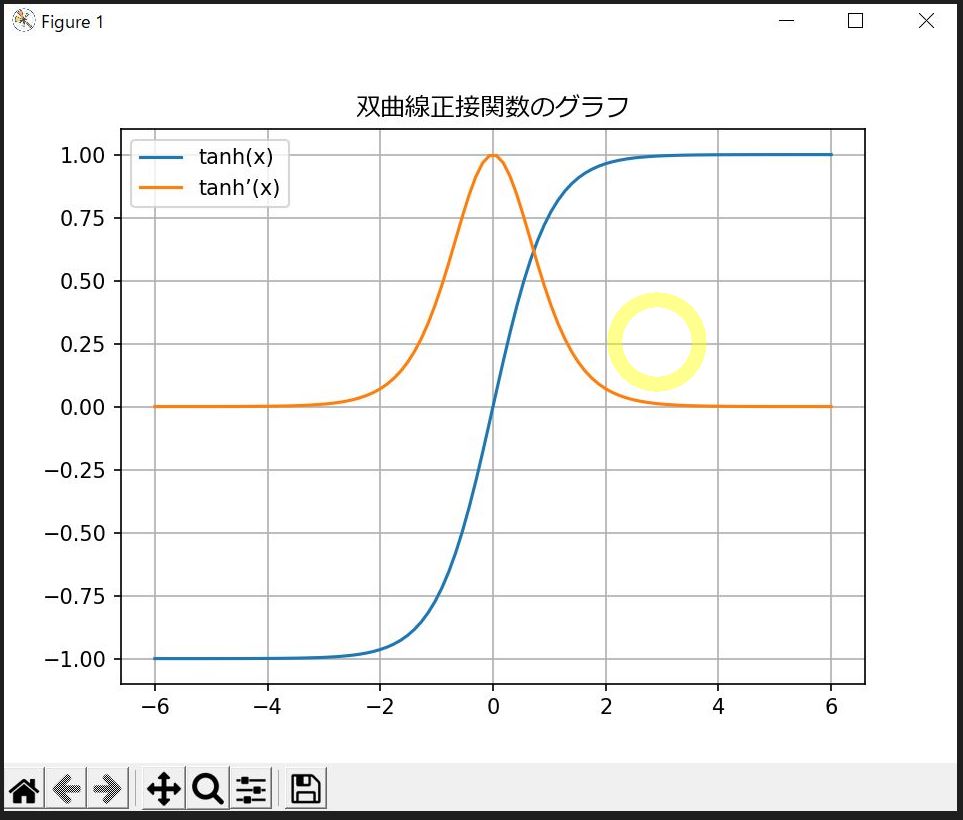
tanh関数（ハイパボリックタンジェント）は、シグモイド関数に似た形状をしていますが、出力範囲が「-1〜1」となっており、勾配がより保たれやすいです。
特にx＝0のときに最大の勾配（1）を持つため、シグモイドよりも勾配消失が起きにくい特性を持ちます。
（図120①）
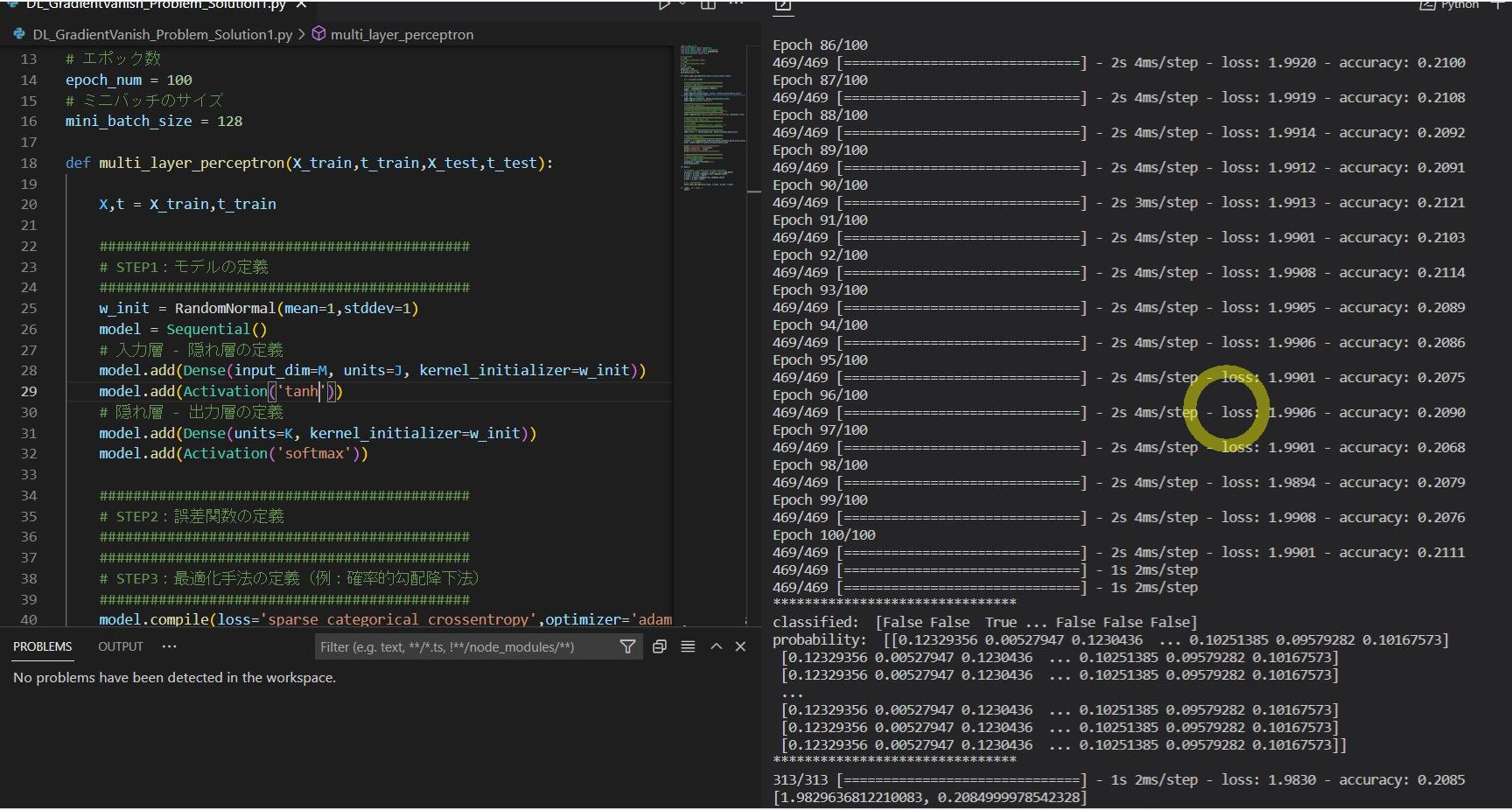
（図121）After（tanh関数を使用）
Epoch 1/100 469/469 [==============================] - 3s 4ms/step - loss: 3.1688 - accuracy: 0.1031 Epoch 2/100 469/469 [==============================] - 2s 4ms/step - loss: 2.3066 - accuracy: 0.1039 ～中略～ Epoch 100/100 469/469 [==============================] - 2s 4ms/step - loss: 1.9901 - accuracy: 0.2111 313/313 [==============================] - 1s 2ms/step - loss: 1.9830 - accuracy: 0.2085 [1.9829636812210083, 0.2084999978542328]
対策②：ReLU
ReLU（Rectified Linear Unit）は、f(x) = max(0, x) で定義され、xが0以下のときは0、xが0より大きいときは1の勾配を持ちます。
この特性により、大きなxに対しても勾配が消失しないため、深層学習でよく利用されます。
また、数式がシンプルで計算効率が良いこともメリットです。
さらに、x<0の領域で微小な勾配を持たせるLeaky ReLUも存在します。
（図131）
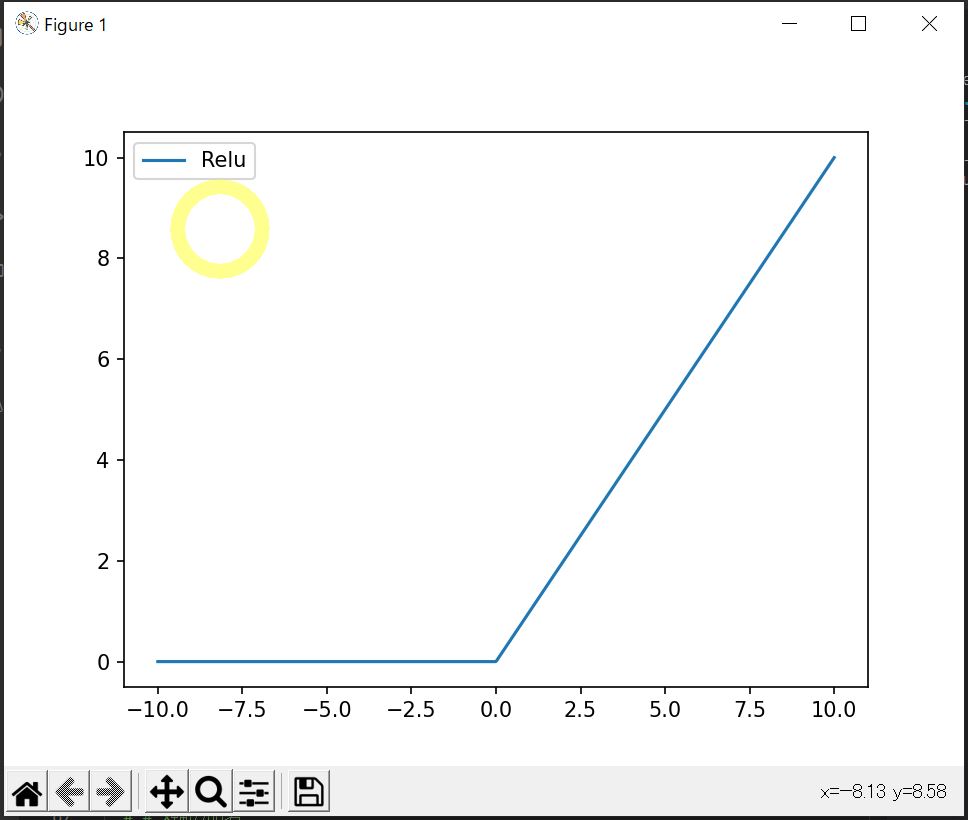
（図122）After（ReLU関数を適用）
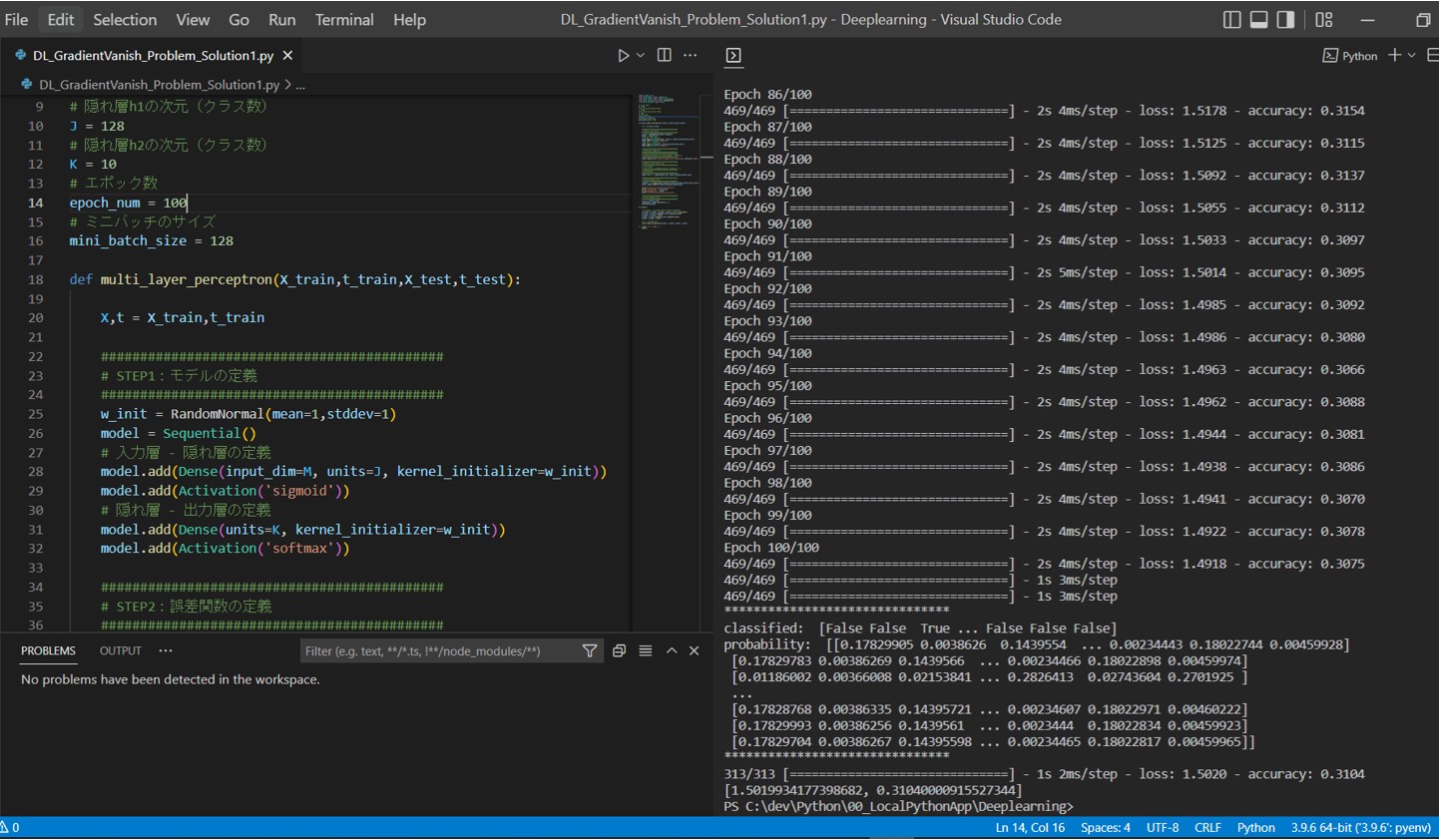
Epoch 1/100 469/469 [==============================] - 2s 4ms/step - loss: 363.2008 - accuracy: 0.4561 Epoch 2/100 469/469 [==============================] - 2s 4ms/step - loss: 12.7101 - accuracy: 0.7627 ～中略～ Epoch 100/100 469/469 [==============================] - 2s 3ms/step - loss: 0.9683 - accuracy: 0.9020 313/313 [==============================] - 1s 2ms/step - loss: 1.4856 - accuracy: 0.8799 [1.4856008291244507, 0.8798999786376953]
