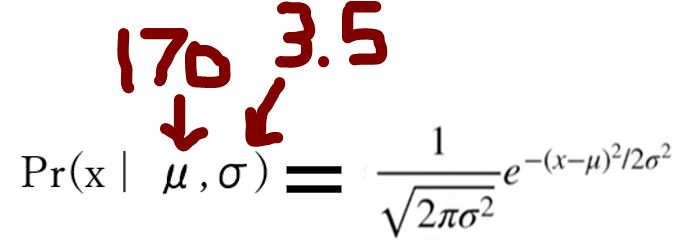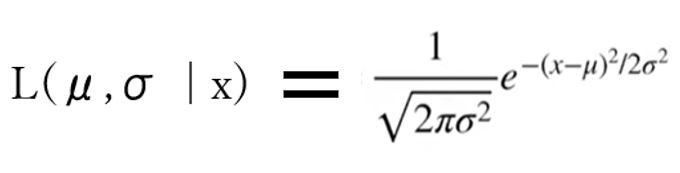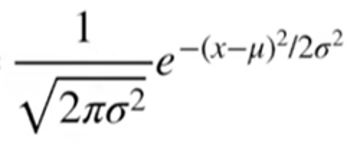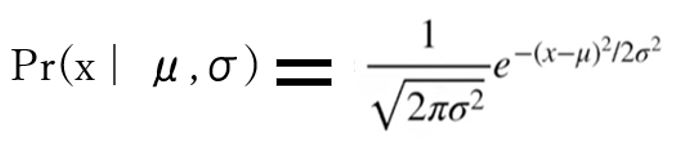<目次>
(1) 確率と尤度の違いとは?概念や数式なども交えて比較紹介
(1-1) 確率:「パラメータ」からデータの「確率」を算出した値?
(1-2) 尤度:「データ」からパラメータの「尤もらしさ」を算出した値
(1-3) 確率と尤度の違い
(1) 確率と尤度の違いとは?概念や数式なども交えて比較紹介
本記事では混乱しがちな概念である「確率」と「尤度」について、それぞれの特徴や違いなどをご紹介します。
(1-1) 確率:「パラメータ」からデータの「確率」を算出した値
●確率の概要(正規分布の例)
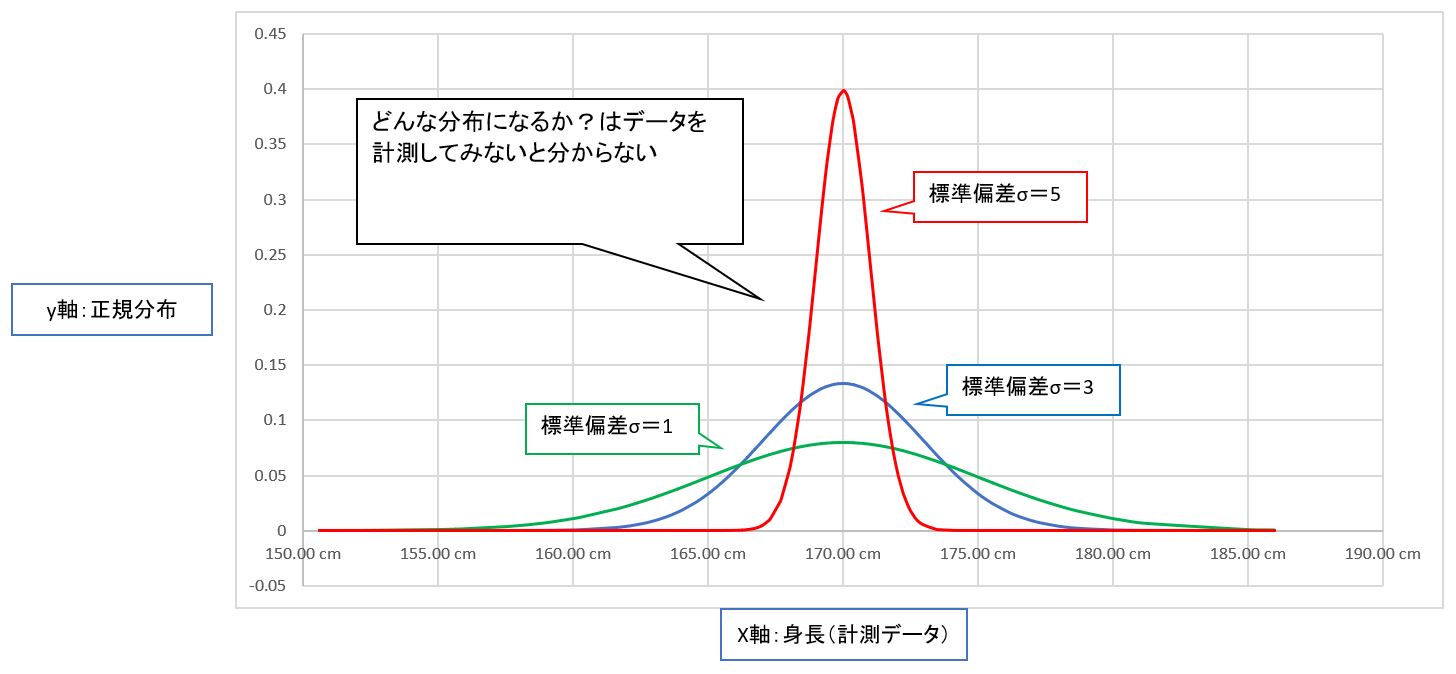
・「分布(distribution)」が与えられており、それに対して「データ」(例:身長、体重)の「発生確率」を求めること。
P([データx1] | [分布パラメータμ,σ])
(図111)
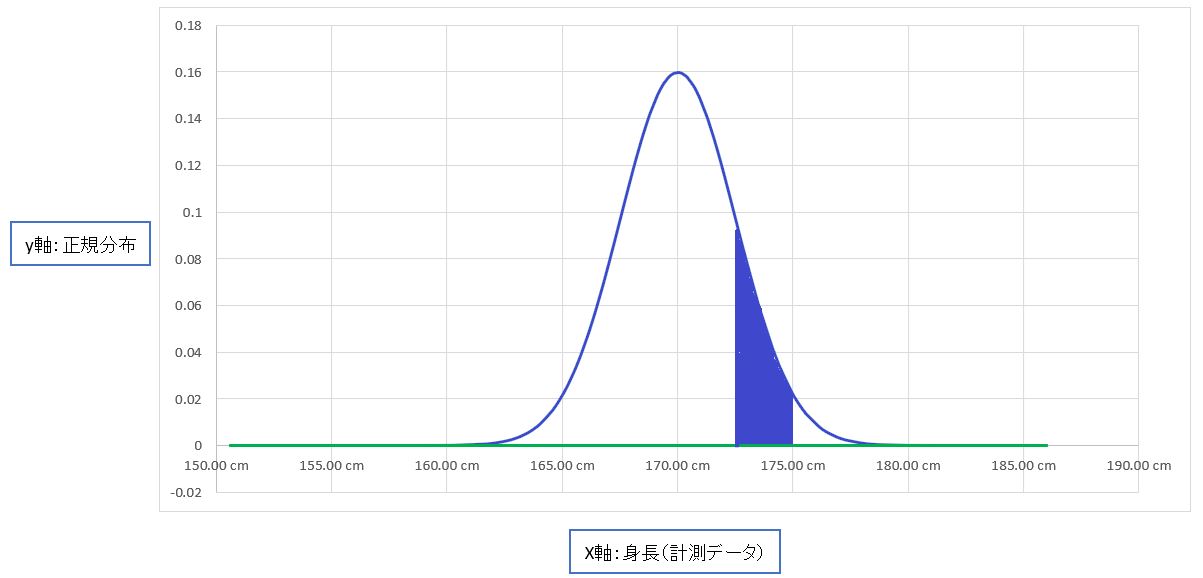
(例)正規分布(例:平均値μ=170cm、標準偏差σ=2.5)から、身長が172.5cm以上&175cm未満である確率を求める
↓
これを数式で表現すると次のようになります。
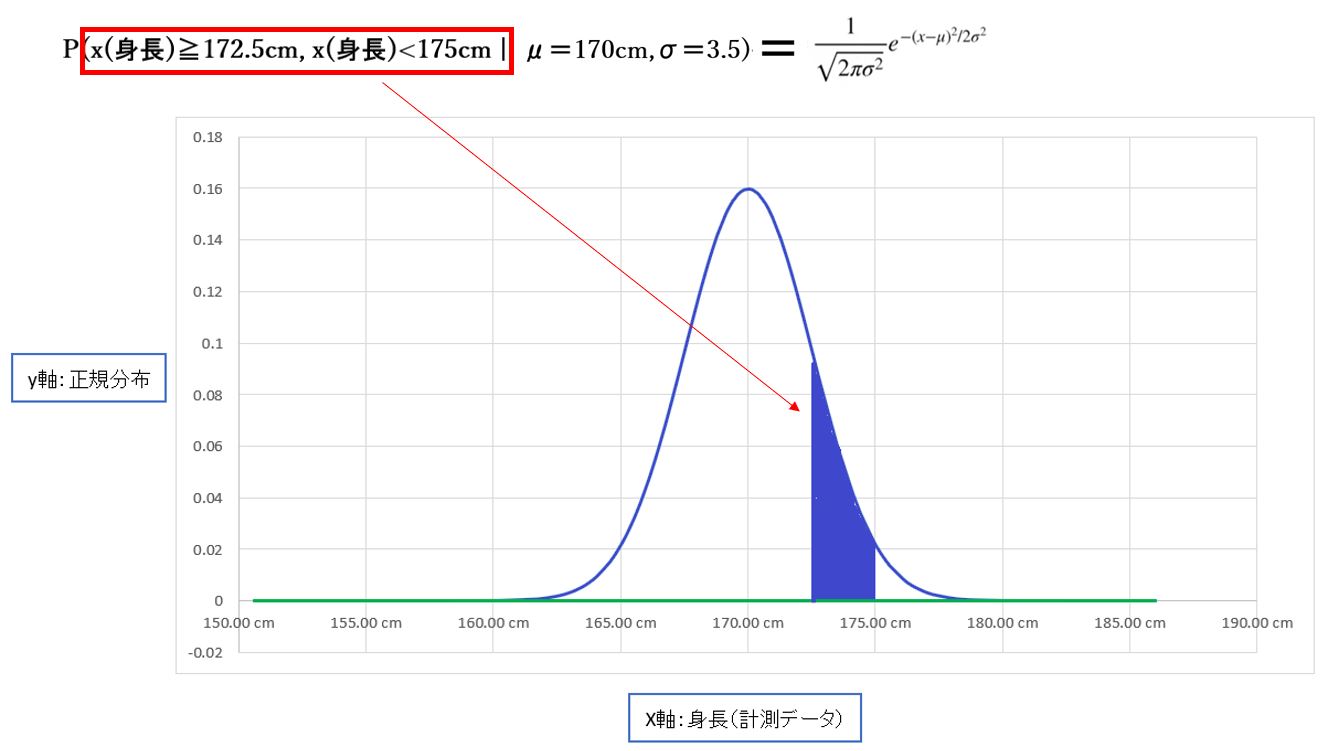
P(身長≧172.5cm, 身長<175cm | μ=170cm,σ=3.5)
真ん中の縦棒(A|B)は「条件付き確率」で「Bが起こった時に、Aが起こる確率」という意味です。
この場合、パラメータ:平均値μ=170cm、標準偏差σ=3.5の場合に、データ条件:172.5cm以上&175cm未満である確率。
→このとき、右側(平均値μ、標準偏差σ)は固定で、左側(172.5cm以上&175cm未満)は可変
(図112)右側は分布の形を司る
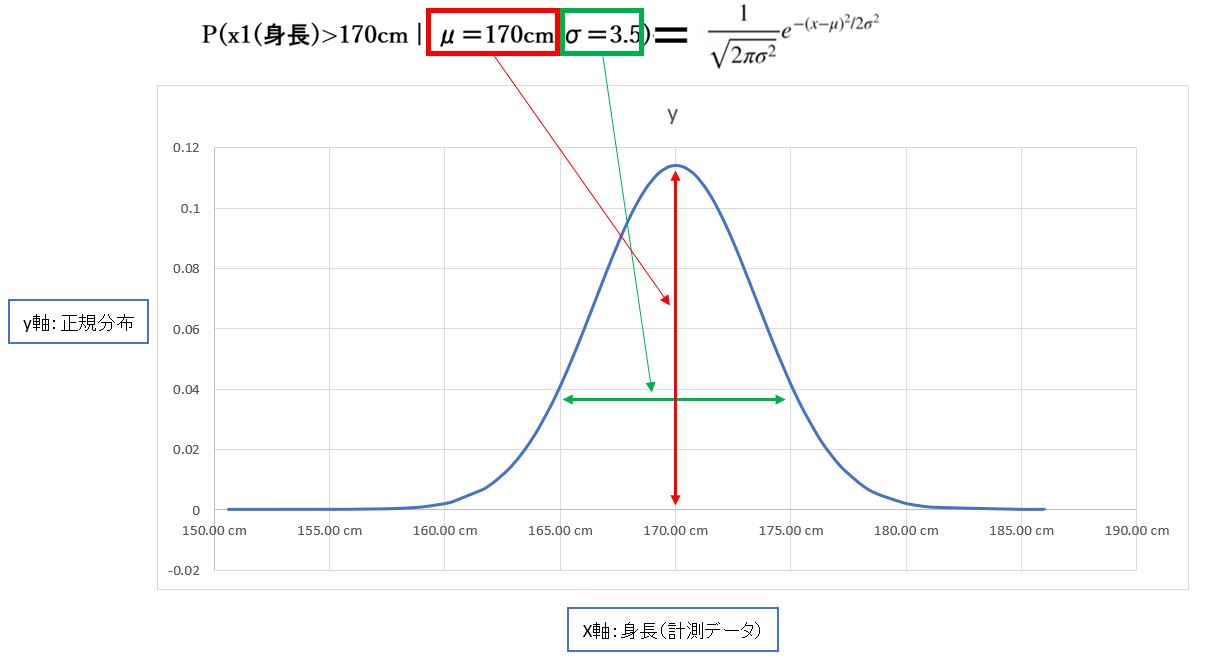
(図113)左側は対象データの曲線配下における領域(≒確率)
●確率の数学的な説明と計算式
・数学的には「確率密度関数(probability density function)」に「パラメータ(例:平均値μ=170cm、標準偏差σ=3.5)」を代入したもの。
(図114)
です。このとき「Pr(x | μ,σ)」は確率密度関数です。
確率密度関数は「確率変数」(≒出る確率が決まっている値)がある値をとる場合の「確率密度」(相対的な出やすさ)を表す関数。「密度」と書かれているのは、X方向の範囲(例:a<x<b)を指定する事で、初めて「確率」が求まる(a<x<bの範囲の曲線の面積)が求まるから。
(図113)左側は対象データの曲線配下における領域(≒確率)

(1-2) 尤度:「データ」からパラメータの「尤もらしさ」を算出した値
●尤度の概要(正規分布の例)
・「データ」(例:身長、体重)に対して「分布(distribution)」の「尤もらしさ」のこと。
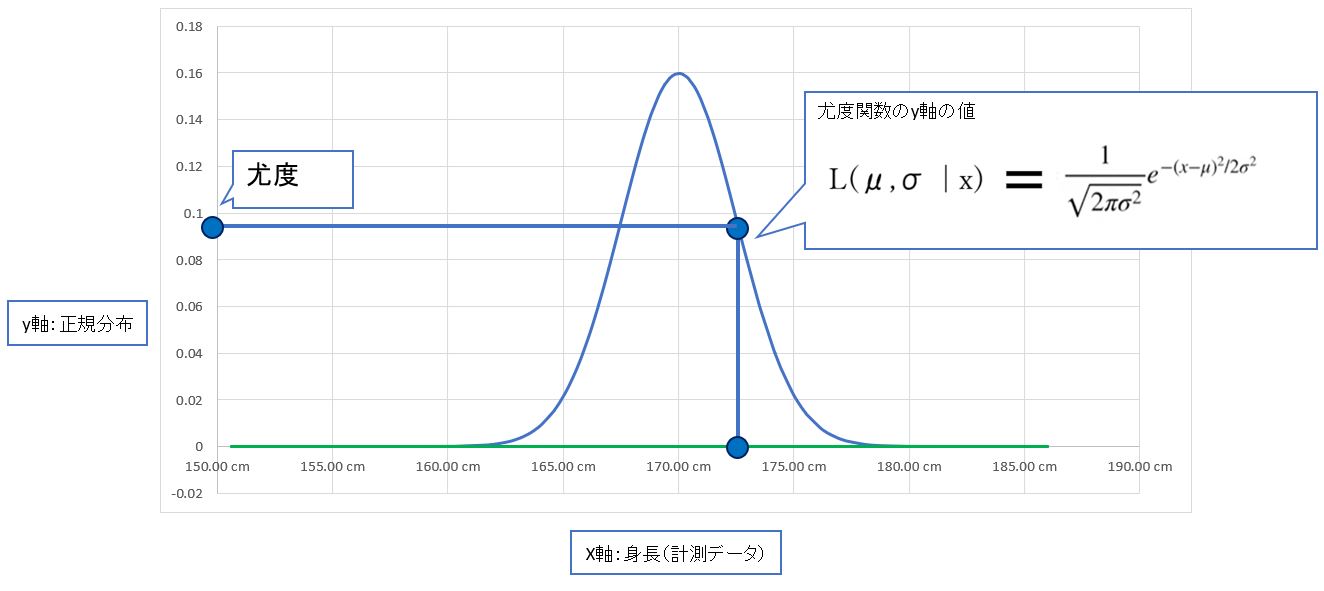
→数学的には尤度関数(平均μ・標準偏差σは片方固定&もう片方は変数扱い)に計測データxを代入した際のy軸の値である
(図121)
⇒μやσが変化させてグラフが移動する際、データ群とグラフが一致するか?を確認するイメージ(データが密集する所が曲線の最大になっているか?全部のデータを総合して尤もらしいか?⇒総乗計算で検証)
(例)身長のデータ条件(172.5cm)から、正規分布(例:平均値μ=170cm、標準偏差σ=2.5)の尤もらしさを計測する(仮定した正規分布がデータに対応するものか?の確からしさ)
↓
これを数式で表現すると次のようになります。
(確率の時と条件が左右逆になっている)
L(μ=170cm,σ=3.5 | 身長=172.5cm)
真ん中の縦棒(A|B)は「条件付き確率」で「Bが起こった時に、Aが起こる確率」という意味です。
この場合、データ条件:身長=170cmの場合に、パラメータ:平均値μ=170cm、標準偏差σ=3.5の正規分布が、尤もらしいか?の度合い。
→このとき、右側(身長=172.5cm)固定で、右側は(平均値μ、標準偏差σ)は可変です。
(図122)左側は分布の形を司る
(図123)右側は測定したデータの値
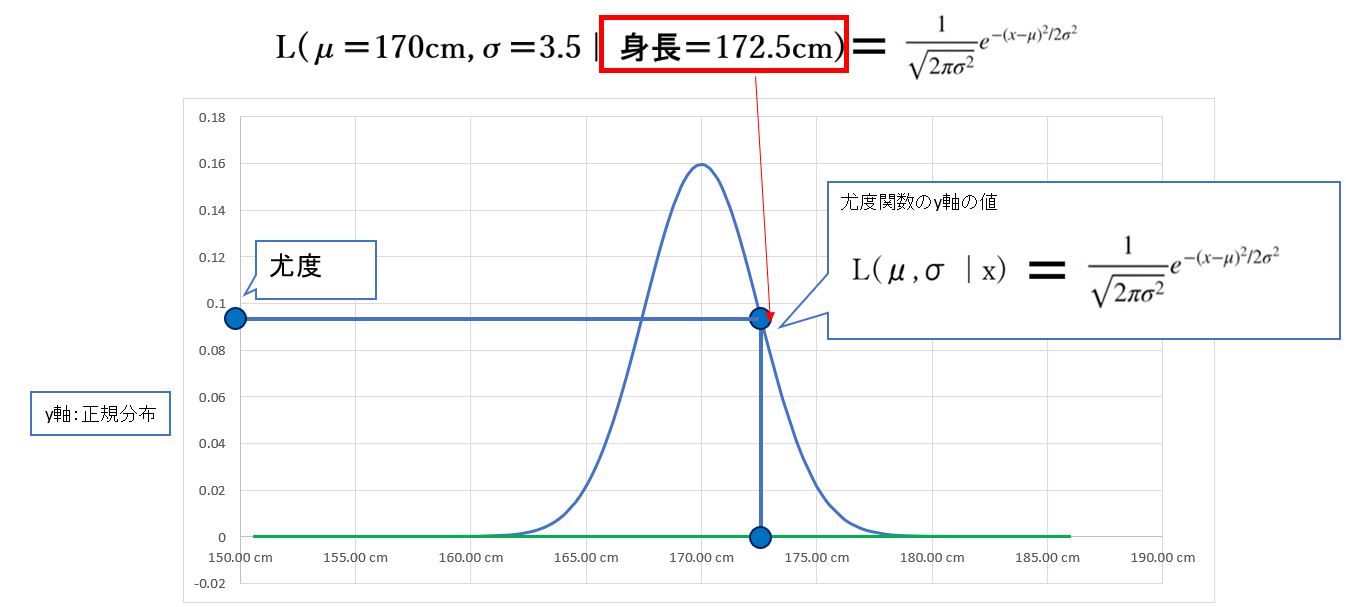
●尤度の数学的な説明と計算式
・数学的には「確率密度関数(probability density function)」に「確率変数(例:身長=170cm)」の観測値を代入したもの。
(図124)
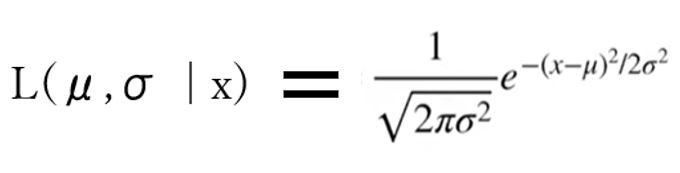
右辺の式そのものは、確率の式と同じであり、次のようにも表現できます。
L(μ,σ | x) = Pr(x | μ,σ)
尤度関数は数学的には確率密度変数「Pr(x | μ,σ)」と同じ式ですが、「確率」を求める際はμ,σを固定→xの確率を求めるのに対し、「尤度」を求める際はxを入力→最適なμ,σを求めるため、逆のような計算をするイメージになります。
(1-3) 確率と尤度の違い
確率:分布とパラメータをINPUTに、データの「確率」を算出したもの
尤度:分布とデータをINPUTに、パラメータの「尤もらしさ」を算出したもの
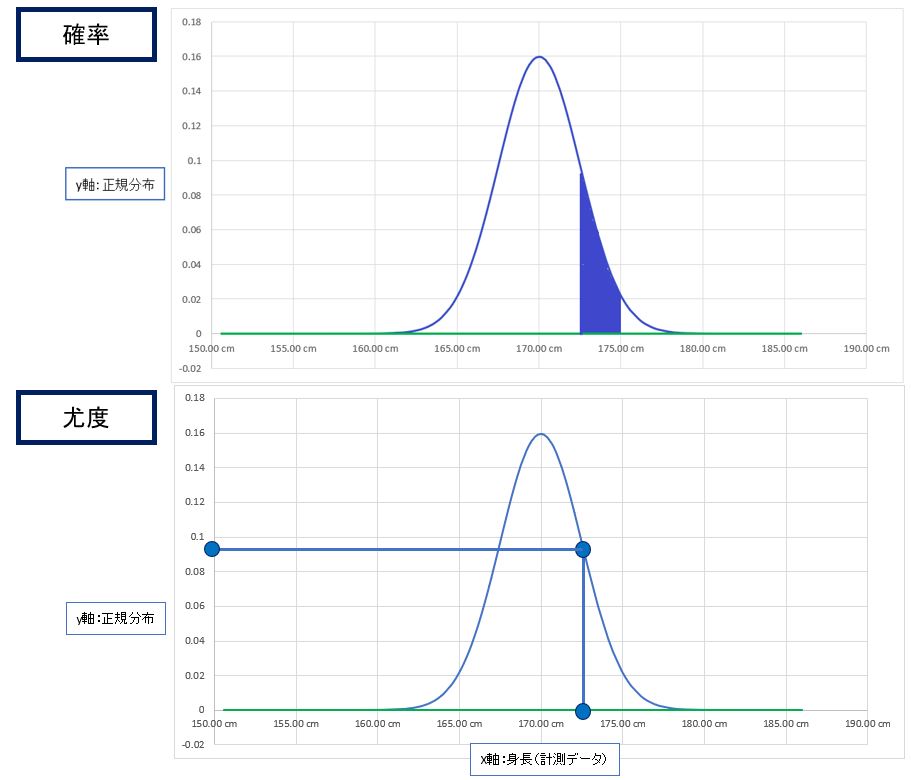
一方で、数学の図形的に見ると次のように言えます。
確率:分布(例:正規分布)を固定(μとσは固定)した際の、分布上のある範囲の面積(=確率)
例:P(身長≧172.5cm, 身長<175cm | μ=170cm,σ=3.5)
尤度:データを固定(例:身長170cm)した際の、分布(例:正規分布)のy軸の値(=尤度)
例:L(μ=170cm,σ=3.5 | 身長=172.5cm)
(図131)
(備考①)
今回は「正規分布」の数式を例にご紹介しましたが、ここでご紹介した「確率」と「尤度」の考え方は全ての「連続確率分布」(例:ガンマ分布、ベータ分布など)にも同様に適用できる。
(図132)
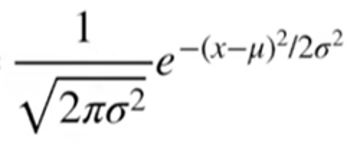
(備考②)標準偏差σについて
正規分布の曲線の形を決めるパラメータです。値が小さいと緩やかで幅広に、値が大きいと急で細くなる。
(図133①)
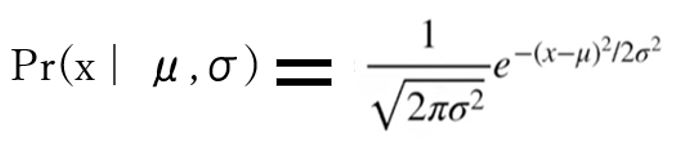
(図134)