ディープラーニングの論理回路とは？Pythonのサンプルプログラムもご紹介

＜目次＞

(１) ディープラーニングの論理回路とは？Pythonのサンプルプログラムもご紹介
　 (１-１) ニューラルネットワークとは？
　(１-２) 論理回路とは？
　(１-３) ANDゲート（論理積）
　(１-４) ORゲート（論理和）
　(１-５) NOTゲート（論理否定）

(１) ディープラーニングの論理回路とは？Pythonのサンプルプログラムもご紹介

ディープラーニングにおいて「論理回路」は３パターンの回路（AND、OR、NOT）の事で、あらゆるパターンに対応できる為に、非常に重要な役割を果たします。

(１-１) ニューラルネットワークとは？

ニューラルネットワークは、人間の脳の機能を模倣し、情報処理やパターン認識のタスクを実行するための数学モデルです。ニューラルネットワークは、多くの繋がった単純なユニット（ニューロン）から構成され、これらのユニットは相互に信号をやり取りすることでデータを処理します。

＞目次にもどる

(１-２) 論理回路とは？

●アナログ回路とデジタル回路

・人間の脳は情報をアナログ（※注１）で処理しているので「アナログ回路」であると言える。

・機械の場合はアナログ回路（例：電話回線など）の他にデジタル回路（例：マイコン）がある

・デジタル回路を用いる事で、自然界の情報をデジタル（0か1）で処理できる（より高速）

・ニューラルネットワークは人間に代わって機械に情報を処理させる試み

・デジタル回路は「0」「1」の入出力を制御するのに「論理ゲート」と呼ばれる回路を使います。

・基本ゲートとして以下３つがあり、この組合せであらゆる入出力のパターンを実現している

　①ANDゲート（論理積）

　②ORゲート（論理和）

　③NOTゲート（論理否定）

（※注１）

・「アナログ回路」は情報が「なめらかで連続値」で処理します（正弦波など）。

・「デジタル回路」は情報を全て「2値（0か1）」に符号化して処理します。

＞目次にもどる

(１-３) ANDゲート（論理積）

●概要

・入力２つ（x1,x2）に対して、出力が１つ（y）。
（図１１０）

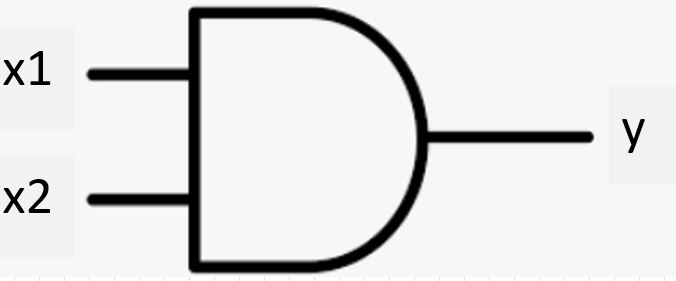
・入出力は以下の通り。

x1, x2, t = 0,0,0
x1, x2, t = 0,1,0
x1, x2, t = 1,0,0
x1, x2, t = 1,1,1

●サンプル

def and_gate(a_w1,a_w2,a_theta):
    
    x1,x2,w1,w2,theta,y,t = 0,0,0,0,0,0,0
    dw1, dw2, dtheta = 0,0,0,
    l_counter, e_counter = 0,0

    # dw1,dw2,dtheataが4回連続0になるまで繰り返し
    #  ⇒ゲートの4パターン全部でデルタ=0なら収束と判断
    while e_counter < 4 and l_counter < 100:
        # ループ変数を更新
        l_counter = l_counter + 1
        
        # x1,x2,tの設定
        # ⇒ゲートの種類に応じて、誤り訂正学習法で使える4つのパターンを設定
        if l_counter%4 == 1:    x1, x2, t = 0,0,0
        elif l_counter%4 == 2:  x1, x2, t = 0,1,0
        elif l_counter%4 == 3:  x1, x2, t = 1,0,0
        else:                   x1, x2, t = 1,1,1

        # w1,w2,thetaの設定
        # 　w1,w2,thetaの初期値は適当な値からスタート可。
        # 　任意の値を設定できるよう、引数として設定
        if l_counter == 0:
            w1,w2,theta = a_w1,a_w2,a_theta
        # 初回以外はデルタ値（dw1,dw2,dtheta）を加算して更新
        else:
            w1 = w1 + dw1
            w2 = w2 + dw2
            theta = theta + dtheta

        # yの計算（モデルの出力）
        if w1*x1 + w2*x2 - theta >= 0:
            y = 1
        else:
            y = 0

        # dw1,dw2,dthetaの計算
        # 初回は0。
        if l_counter == 0:
            dw1,dw2,dtheta = 0,0,0
        # 初回以降はモデルの出力(y)と正解の出力(t)の
        # 差を用いて計算する。
        else:
            dw1 = (t-y)*x1
            dw2 = (t-y)*x2
            dtheta = (-1)*(t-y)

        # ループ脱出判定
        # ゲートの4パターン(x1,x2,tの組み合わせ)全てで
        # 修正分(dw1,dw2,dtheta)が0になった場合に脱出
        # この4パターンのカウントを「l_counter」が担う。
        # 4パターンの1つでもＮＧの場合、l_counterをリセット(if分岐)
        if dw1 == 0 and dw2 == 0 and dtheta == 0:
            e_counter = e_counter + 1
        if l_counter%4 == 0 and e_counter > 0 and e_counter < 4:
            e_counter = 0

        print("k= ",l_counter,"x1 =",x1,"x2 =",x2,"t =",t,"w1 =",w1,"w2 =",w2,"theta =",theta,"y =",y,"dw1 =",dw1,"dw2 =",dw2,"dtheta =",dtheta,"end=",e_counter)

def main():
    # w1,w2,thetaの適当な初期値を設定して
    # 誤り訂正学習法を実行。
    and_gate(1,1,1)

if __name__ == "__main__":
    main()

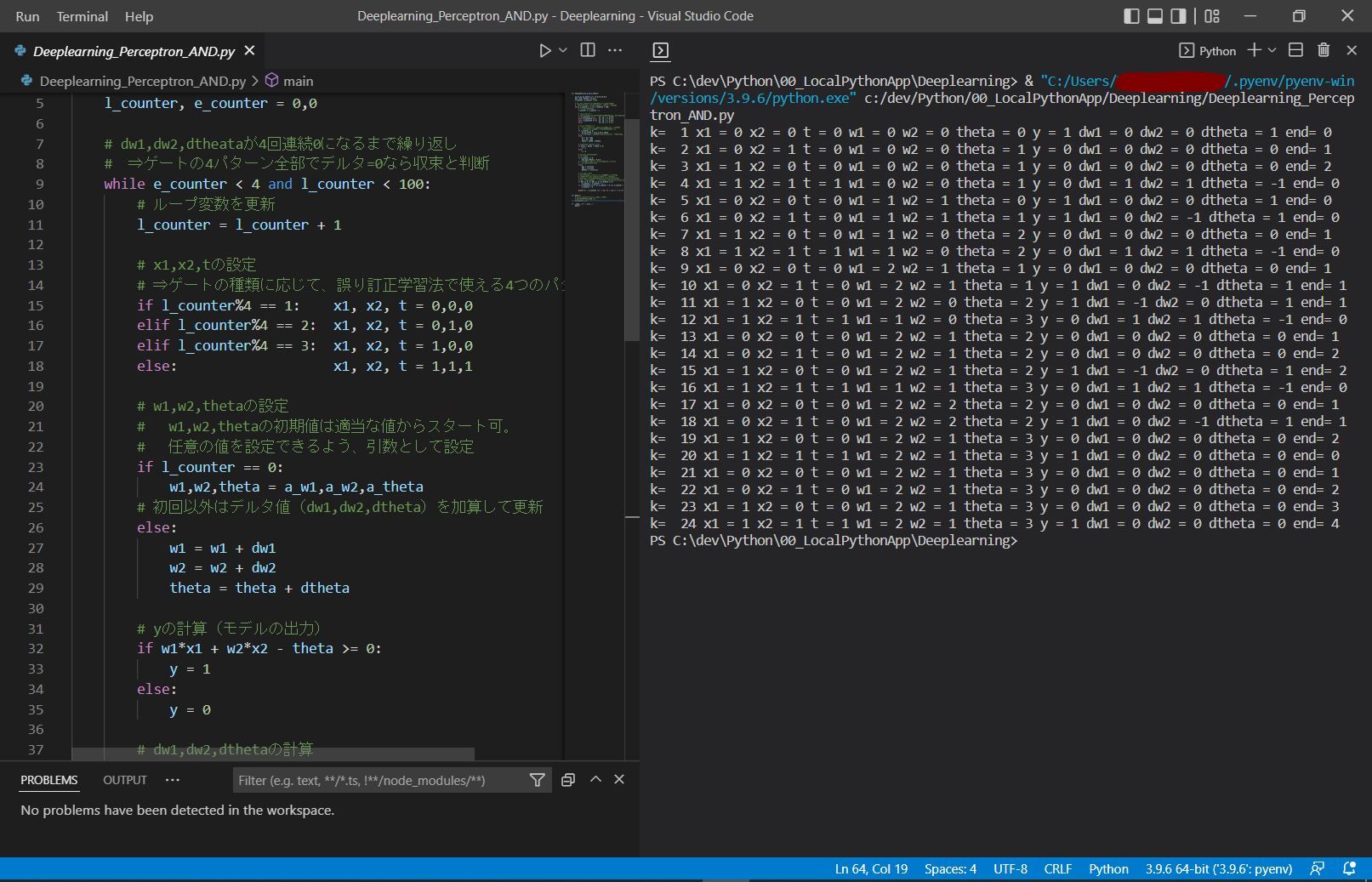
●出力例＆まとめ

k=  1 x1 = 0 x2 = 0 t = 0 w1 = 0 w2 = 0 theta = 0 y = 1 dw1 = 0 dw2 = 0 dtheta = 1 end= 0
k=  2 x1 = 0 x2 = 1 t = 0 w1 = 0 w2 = 0 theta = 1 y = 0 dw1 = 0 dw2 = 0 dtheta = 0 end= 1  
k=  3 x1 = 1 x2 = 0 t = 0 w1 = 0 w2 = 0 theta = 1 y = 0 dw1 = 0 dw2 = 0 dtheta = 0 end= 2  
k=  4 x1 = 1 x2 = 1 t = 1 w1 = 0 w2 = 0 theta = 1 y = 0 dw1 = 1 dw2 = 1 dtheta = -1 end= 0 
k=  5 x1 = 0 x2 = 0 t = 0 w1 = 1 w2 = 1 theta = 0 y = 1 dw1 = 0 dw2 = 0 dtheta = 1 end= 0  
k=  6 x1 = 0 x2 = 1 t = 0 w1 = 1 w2 = 1 theta = 1 y = 1 dw1 = 0 dw2 = -1 dtheta = 1 end= 0 
k=  7 x1 = 1 x2 = 0 t = 0 w1 = 1 w2 = 0 theta = 2 y = 0 dw1 = 0 dw2 = 0 dtheta = 0 end= 1  
k=  8 x1 = 1 x2 = 1 t = 1 w1 = 1 w2 = 0 theta = 2 y = 0 dw1 = 1 dw2 = 1 dtheta = -1 end= 0 
k=  9 x1 = 0 x2 = 0 t = 0 w1 = 2 w2 = 1 theta = 1 y = 0 dw1 = 0 dw2 = 0 dtheta = 0 end= 1  
k=  10 x1 = 0 x2 = 1 t = 0 w1 = 2 w2 = 1 theta = 1 y = 1 dw1 = 0 dw2 = -1 dtheta = 1 end= 1
k=  11 x1 = 1 x2 = 0 t = 0 w1 = 2 w2 = 0 theta = 2 y = 1 dw1 = -1 dw2 = 0 dtheta = 1 end= 1
k=  12 x1 = 1 x2 = 1 t = 1 w1 = 1 w2 = 0 theta = 3 y = 0 dw1 = 1 dw2 = 1 dtheta = -1 end= 0
k=  13 x1 = 0 x2 = 0 t = 0 w1 = 2 w2 = 1 theta = 2 y = 0 dw1 = 0 dw2 = 0 dtheta = 0 end= 1 
k=  14 x1 = 0 x2 = 1 t = 0 w1 = 2 w2 = 1 theta = 2 y = 0 dw1 = 0 dw2 = 0 dtheta = 0 end= 2 
k=  15 x1 = 1 x2 = 0 t = 0 w1 = 2 w2 = 1 theta = 2 y = 1 dw1 = -1 dw2 = 0 dtheta = 1 end= 2
k=  16 x1 = 1 x2 = 1 t = 1 w1 = 1 w2 = 1 theta = 3 y = 0 dw1 = 1 dw2 = 1 dtheta = -1 end= 0
k=  17 x1 = 0 x2 = 0 t = 0 w1 = 2 w2 = 2 theta = 2 y = 0 dw1 = 0 dw2 = 0 dtheta = 0 end= 1 
k=  18 x1 = 0 x2 = 1 t = 0 w1 = 2 w2 = 2 theta = 2 y = 1 dw1 = 0 dw2 = -1 dtheta = 1 end= 1
k=  19 x1 = 1 x2 = 0 t = 0 w1 = 2 w2 = 1 theta = 3 y = 0 dw1 = 0 dw2 = 0 dtheta = 0 end= 2 
k=  20 x1 = 1 x2 = 1 t = 1 w1 = 2 w2 = 1 theta = 3 y = 1 dw1 = 0 dw2 = 0 dtheta = 0 end= 0 
k=  21 x1 = 0 x2 = 0 t = 0 w1 = 2 w2 = 1 theta = 3 y = 0 dw1 = 0 dw2 = 0 dtheta = 0 end= 1 
k=  22 x1 = 0 x2 = 1 t = 0 w1 = 2 w2 = 1 theta = 3 y = 0 dw1 = 0 dw2 = 0 dtheta = 0 end= 2 
k=  23 x1 = 1 x2 = 0 t = 0 w1 = 2 w2 = 1 theta = 3 y = 0 dw1 = 0 dw2 = 0 dtheta = 0 end= 3 
k=  24 x1 = 1 x2 = 1 t = 1 w1 = 2 w2 = 1 theta = 3 y = 1 dw1 = 0 dw2 = 0 dtheta = 0 end= 4

⇒「w1 = 2 w2 = 1 theta =3」から、2*x1 + 1*x2 – 3 = 0がニューロンが発火するかどうか？の境界線となります（分離境界の直線は複数あり、これはあくまで一例）

（図１１１）

＞目次にもどる

(１-４) ORゲート（論理和）

●概要

・AND同様、入力２つ（x1,x2）に対して、出力が１つ（y）。

（図１２０）

・入出力は以下の通り。

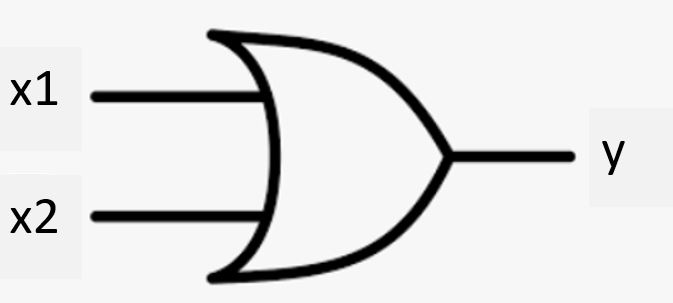
x1, x2, t = 0,0,0
x1, x2, t = 0,1,1
x1, x2, t = 1,0,1
x1, x2, t = 1,1,1

●サンプル

ANDゲートのプログラムを下記のように修正するのみです。

（Before）

      # x1,x2,tの設定
        # ⇒ゲートの種類に応じて、誤り訂正学習法で使える4つのパターンを設定
        if l_counter%4 == 1:    x1, x2, t = 0,0,0
        elif l_counter%4 == 2:  x1, x2, t = 0,1,0
        elif l_counter%4 == 3:  x1, x2, t = 1,0,0
        else:                   x1, x2, t = 1,1,1

↓
（After）

        # x1,x2,tの設定
        # ⇒ゲートの種類に応じて、誤り訂正学習法で使える4つのパターンを設定
        if l_counter%4 == 1:    x1, x2, t = 0,0,0
        elif l_counter%4 == 2:  x1, x2, t = 0,1,1
        elif l_counter%4 == 3:  x1, x2, t = 1,0,1
        else:                   x1, x2, t = 1,1,1

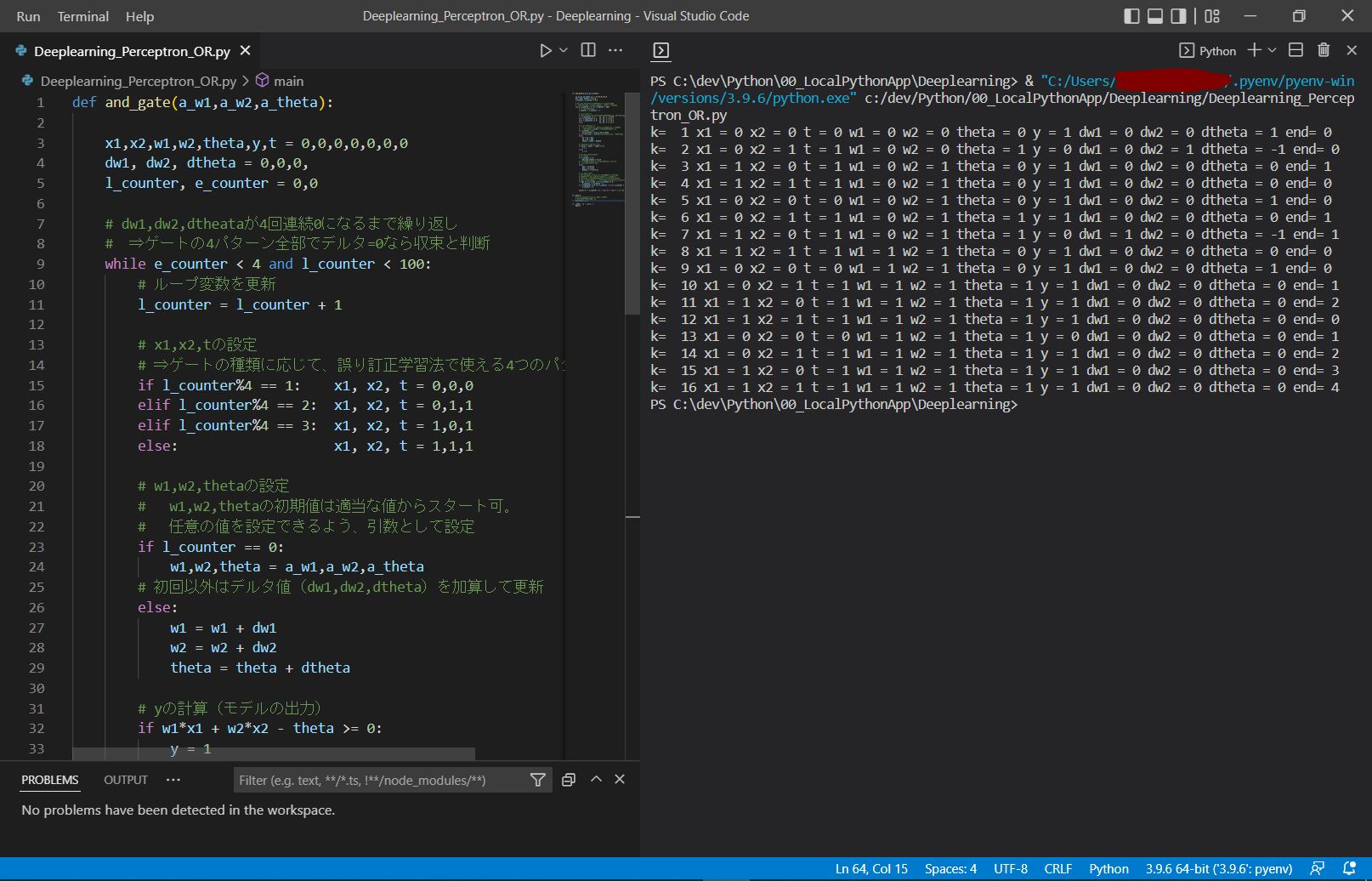
●出力例

k=  1 x1 = 0 x2 = 0 t = 0 w1 = 0 w2 = 0 theta = 0 y = 1 dw1 = 0 dw2 = 0 dtheta = 1 end= 0
k=  2 x1 = 0 x2 = 1 t = 1 w1 = 0 w2 = 0 theta = 1 y = 0 dw1 = 0 dw2 = 1 dtheta = -1 end= 0
k=  3 x1 = 1 x2 = 0 t = 1 w1 = 0 w2 = 1 theta = 0 y = 1 dw1 = 0 dw2 = 0 dtheta = 0 end= 1 
k=  4 x1 = 1 x2 = 1 t = 1 w1 = 0 w2 = 1 theta = 0 y = 1 dw1 = 0 dw2 = 0 dtheta = 0 end= 0 
k=  5 x1 = 0 x2 = 0 t = 0 w1 = 0 w2 = 1 theta = 0 y = 1 dw1 = 0 dw2 = 0 dtheta = 1 end= 0 
k=  6 x1 = 0 x2 = 1 t = 1 w1 = 0 w2 = 1 theta = 1 y = 1 dw1 = 0 dw2 = 0 dtheta = 0 end= 1 
k=  7 x1 = 1 x2 = 0 t = 1 w1 = 0 w2 = 1 theta = 1 y = 0 dw1 = 1 dw2 = 0 dtheta = -1 end= 1
k=  8 x1 = 1 x2 = 1 t = 1 w1 = 1 w2 = 1 theta = 0 y = 1 dw1 = 0 dw2 = 0 dtheta = 0 end= 0 
k=  9 x1 = 0 x2 = 0 t = 0 w1 = 1 w2 = 1 theta = 0 y = 1 dw1 = 0 dw2 = 0 dtheta = 1 end= 0 
k=  10 x1 = 0 x2 = 1 t = 1 w1 = 1 w2 = 1 theta = 1 y = 1 dw1 = 0 dw2 = 0 dtheta = 0 end= 1
k=  11 x1 = 1 x2 = 0 t = 1 w1 = 1 w2 = 1 theta = 1 y = 1 dw1 = 0 dw2 = 0 dtheta = 0 end= 2
k=  12 x1 = 1 x2 = 1 t = 1 w1 = 1 w2 = 1 theta = 1 y = 1 dw1 = 0 dw2 = 0 dtheta = 0 end= 0
k=  13 x1 = 0 x2 = 0 t = 0 w1 = 1 w2 = 1 theta = 1 y = 0 dw1 = 0 dw2 = 0 dtheta = 0 end= 1
k=  14 x1 = 0 x2 = 1 t = 1 w1 = 1 w2 = 1 theta = 1 y = 1 dw1 = 0 dw2 = 0 dtheta = 0 end= 2
k=  15 x1 = 1 x2 = 0 t = 1 w1 = 1 w2 = 1 theta = 1 y = 1 dw1 = 0 dw2 = 0 dtheta = 0 end= 3
k=  16 x1 = 1 x2 = 1 t = 1 w1 = 1 w2 = 1 theta = 1 y = 1 dw1 = 0 dw2 = 0 dtheta = 0 end= 4

⇒「w1 = 1 w2 = 1 theta =1」から、1*x1 + 1*x2 – 1 = 0がニューロンが発火するかどうか？の境界線となります（分離境界の直線は複数あり、これはあくまで一例）

（図１２１）

＞目次にもどる

(１-５) NOTゲート（論理否定）

●概要

ANDやORと異なり、入力が１つのみ（x1）。出力は他と同様で１つ（y）。
（図１３０）

・入出力は以下の通り。

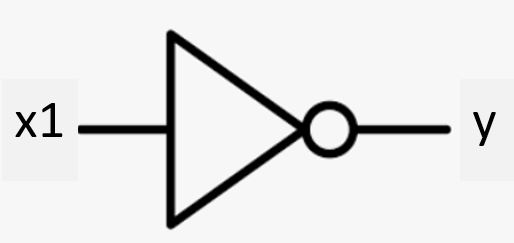
x1, t = 0,1
x1, t = 1,0

●サンプル

def not_gate(a_w1,a_theta):
    
    x1,w1,theta,y,t = 0,0,0,0,0,
    dw1, dtheta = 0,0
    l_counter, e_counter = 0,0

    # dw1,dw2,dtheataが2回連続0になるまで繰り返し
    #  ⇒ゲートの2パターン全部でデルタ=0なら収束と判断
    while e_counter < 2 and l_counter < 100:
        # ループ変数を更新
        l_counter = l_counter + 1
        
        # x1,x2,tの設定
        # ⇒ゲートの種類に応じて、誤り訂正学習法で使える4つのパターンを設定
        if l_counter%2 == 1:    x1, t = 0,1
        else:                   x1, t = 1,0

        # w1,w2,thetaの設定
        # 　w1,w2,thetaの初期値は適当な値からスタート可。
        # 　任意の値を設定できるよう、引数として設定
        if l_counter == 0:
            w1,theta = a_w1,a_theta
        # 初回以外はデルタ値（dw1,dw2,dtheta）を加算して更新
        else:
            w1 = w1 + dw1
            theta = theta + dtheta

        # yの計算（モデルの出力）
        if w1*x1 - theta >= 0:
            y = 1
        else:
            y = 0

        # dw1,dw2,dthetaの計算
        # 初回は0。
        if l_counter == 0:
            dw1,dtheta = 0,0
        # 初回以降はモデルの出力(y)と正解の出力(t)の
        # 差を用いて計算する。
        else:
            dw1 = (t-y)*x1
            dtheta = (-1)*(t-y)

        # ループ脱出判定
        # ゲートの2パターン(x1,tの組み合わせ)全てで
        # 修正分(dw1,dtheta)が0になった場合に脱出
        # この2パターンのカウントを「l_counter」が担う。
        # 2パターンの1つでもＮＧの場合、l_counterをリセット(if分岐)
        if dw1 == 0 and dtheta == 0:
            e_counter = e_counter + 1
        if l_counter%2 == 0 and e_counter > 0 and e_counter < 2:
            e_counter = 0

        print("k= ",l_counter,"x1 =",x1,"t =",t,"w1 =",w1,"theta =",theta,"y =",y,"dw1 =",dw1,"dtheta =",dtheta,"end=",e_counter)

def main():
    # w1,w2,thetaの適当な初期値を設定して
    # 誤り訂正学習法を実行。
    not_gate(1,1)

if __name__ == "__main__":
    main()

●出力例

k=  1 x1 = 0 t = 1 w1 = 0 theta = 0 y = 1 dw1 = 0 dtheta = 0 end= 1
k=  2 x1 = 1 t = 0 w1 = 0 theta = 0 y = 1 dw1 = -1 dtheta = 1 end= 0 
k=  3 x1 = 0 t = 1 w1 = -1 theta = 1 y = 0 dw1 = 0 dtheta = -1 end= 0
k=  4 x1 = 1 t = 0 w1 = -1 theta = 0 y = 0 dw1 = 0 dtheta = 0 end= 0 
k=  5 x1 = 0 t = 1 w1 = -1 theta = 0 y = 1 dw1 = 0 dtheta = 0 end= 1 
k=  6 x1 = 1 t = 0 w1 = -1 theta = 0 y = 0 dw1 = 0 dtheta = 0 end= 2

（図１３１）

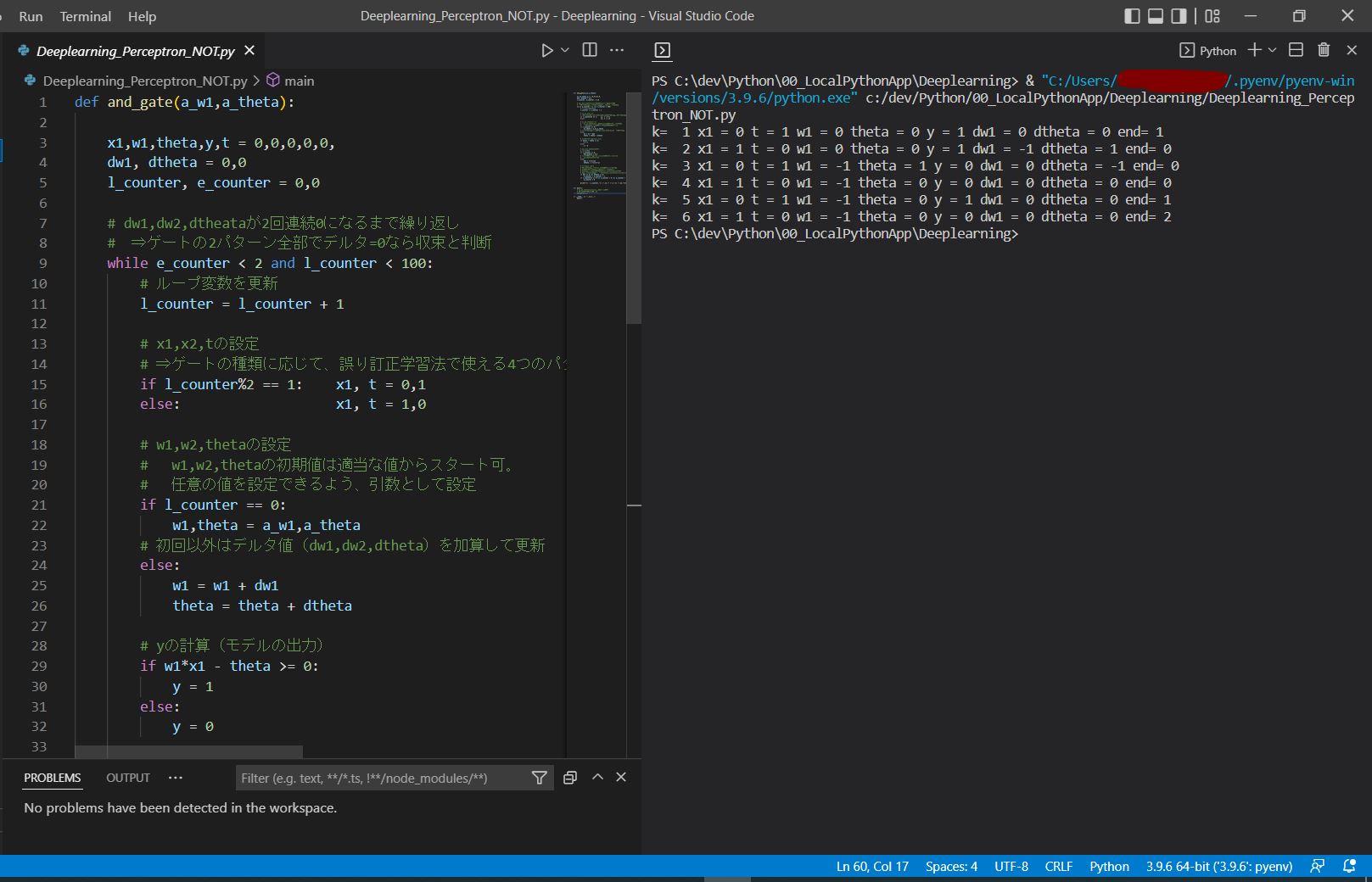
これら３つの論理ゲートの組み合わせで、様々なパターンに対応できる。

＞目次にもどる