ディープラーニングのモデルの評価とは？実際のPythonプログラムもご紹介

＜目次＞

ディープラーニングのモデルの評価とは？実際のPythonプログラムもご紹介
　 (１-１) モデルの評価の概要
　 (１-２) モデルの評価の指標
　 (１-３) モデルの評価の実装例①
　(１-４) モデルの評価の実装例②（Keras）

ディープラーニングのモデルの評価とは？実際のPythonプログラムもご紹介

(１-１) モデルの評価の概要

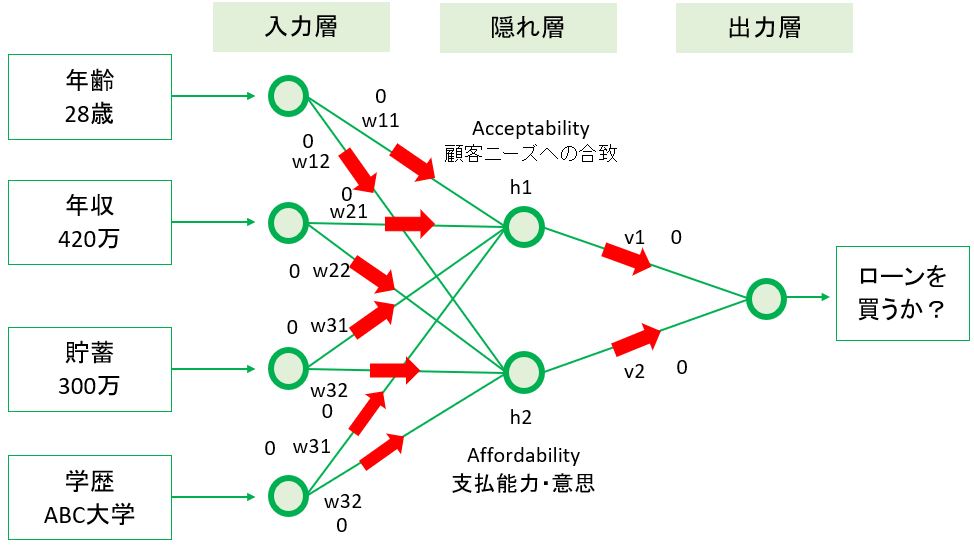
実世界のデータは異常値やノイズが混じっているのが当たり前です。よって100%キレイな分類は不可であり、可能な限り「最善」の分類を目指します。

（図１１０）ノイズの混じったデータ例

「最善」とは、データが持つパターンを見つけ出すこと。多少分類から外れていても、傾向を掴めていれば最善とみなせます。つまり「次回、似たデータを与えられた時に正解できるか？」が重要です。

導き出した予測を「評価」するためには「学習に使ったデータ以外の未知のデータ＝テストデータ」を使います。一方、学習に使うデータはトレーニングデータと呼ばれます。未知のデータが手に入らないケースもあるため、手元のデータをランダムにトレーニングとテストに分けて使用します。

（図１１１）

●「評価」までの流れ

・データをトレーニング用/評価用に分割
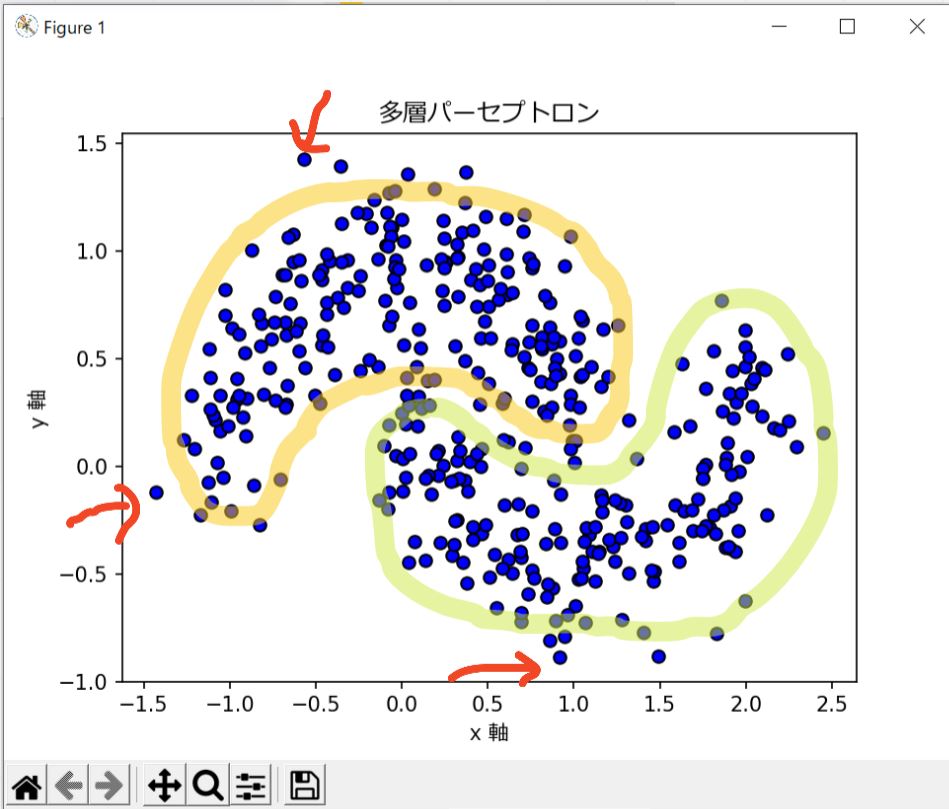
（図１２１）

・トレーニングデータで学習
（図１２２）

・テストデータで評価
（図１２３）

＞目次にもどる

(１-２) モデルの評価の指標

代表的な評価指標には「正解率（Accuracy）」「適合率（Precision）」「再現率（Recall）」があります。以下、犬or猫の2値分類を例に説明します。

（図１３１）

正解値tと出力yの組合せの名前：

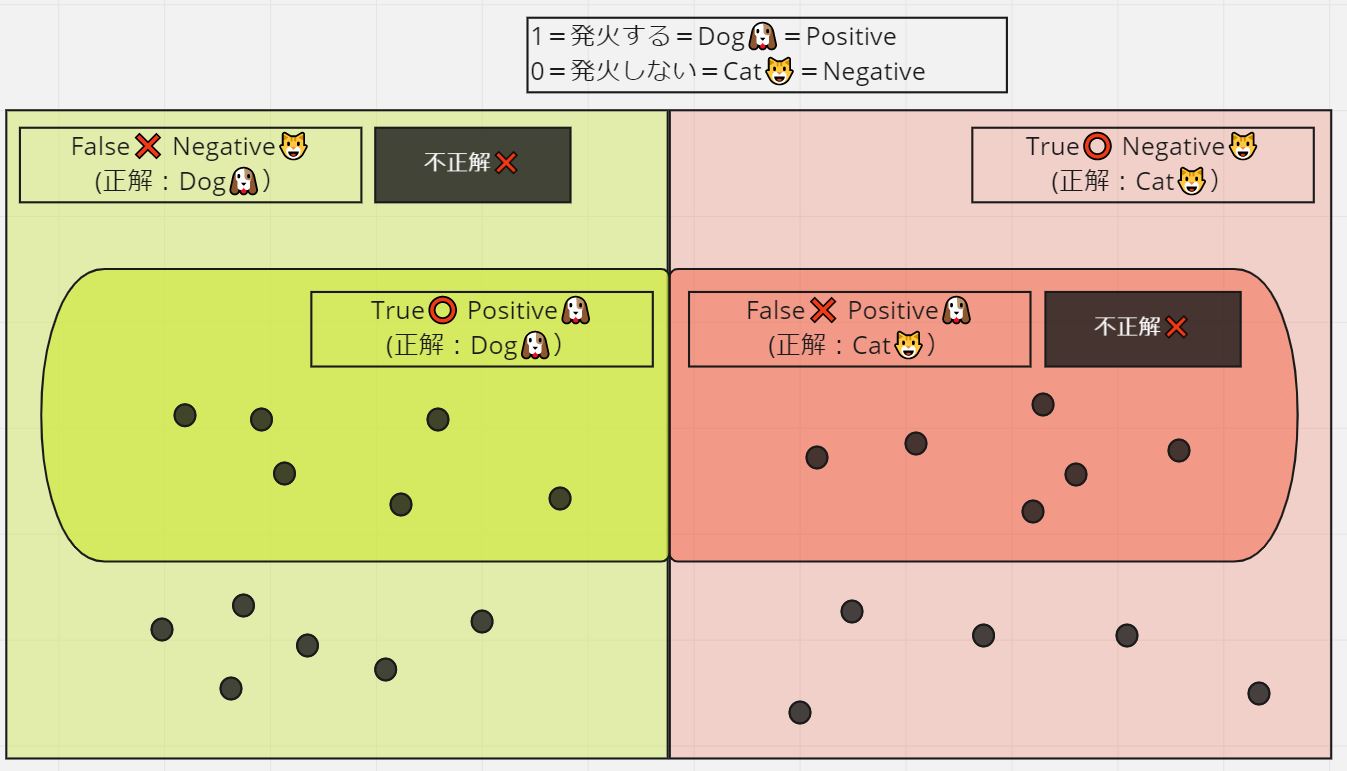
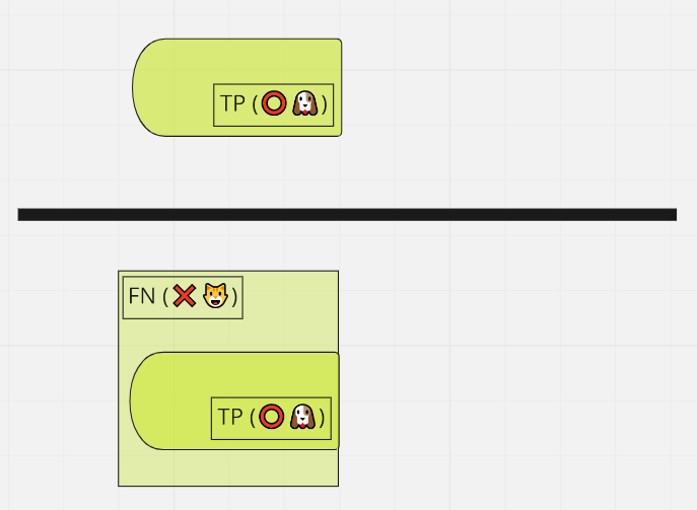
True Positive：正解、y＝犬
False Positive：不正解、y＝犬
True Negative：正解、y＝猫
False Negative：不正解、y＝猫

（図１３２）

正解率（Accuracy）
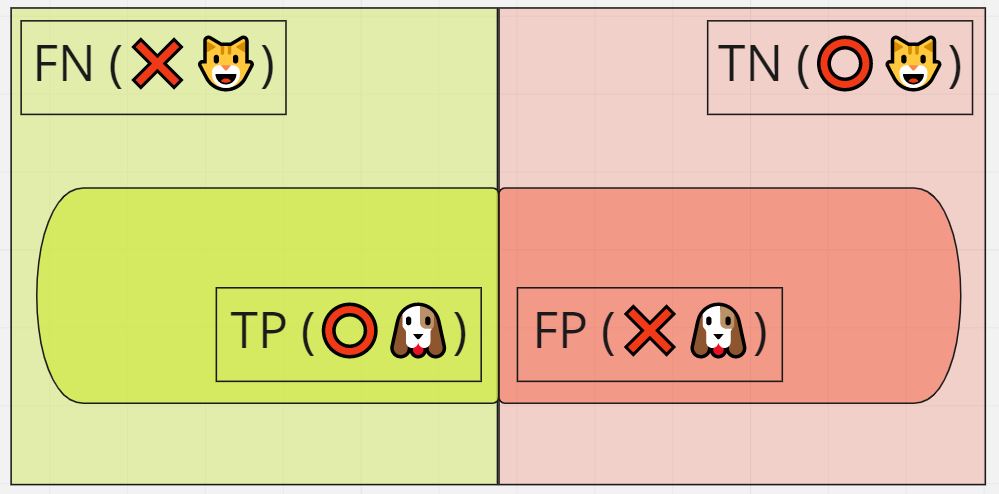
式：(TP+TN)/(TP+FP+FN+TN)
意味：全データの中で正しく予測した割合
（図１３３）

適合率（Precision）
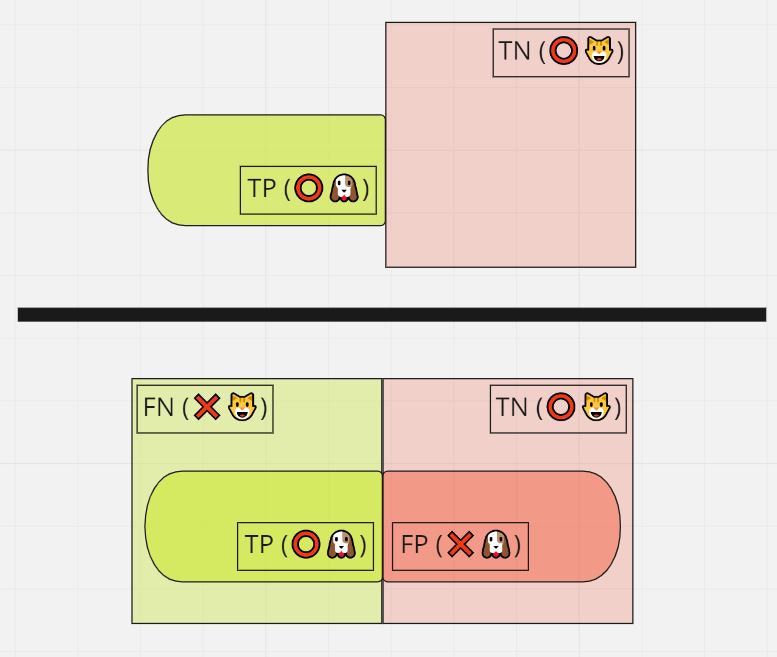
式：TP/(TP+FP)
意味：「発火した」データの中で「発火すべき」だった割合
（図１３４）

再現率（Recall）
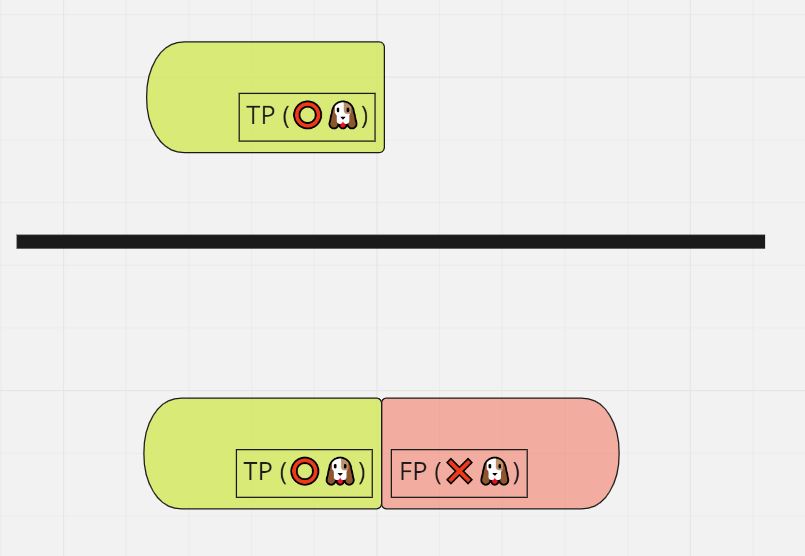
式：TP/(TP+FN)
意味：「発火すべき」データの中で実際に「発火した」割合
（図１３５）

＞目次にもどる

(１-３) モデルの評価の実装例①

「こちらの記事」で紹介した多層パーセプトロンのPython実装に、評価ロジックを追加した例を以下に示します。

############################################
# STEP6：評価
############################################
# ■ multi_layer_perceptron_evaluate()
# 　テストデータを用いてモデルの評価を行う（Accuracyの算出）
# ■ 引数（例）
#   X_arg = テストデータ[N×M]
#   t_arg = 正解データ[N×K]
#   W_arg = 学習結果W [J×M]
#   b_arg = 学習結果b [J×1]
#   V_arg = 学習結果V [K×J]
#   c_arg = 学習結果c [K×1]
# ■ 用途（例）
# 　学習済みのモデルの評価（Accuracyの算出）

def multi_layer_perceptron_evaluate(X_arg,t_arg,W_arg,b_arg,V_arg,c_arg):

    # データセットの規模を取得
    N = X_arg.shape[0]

    # 入力の電気信号Xの初期化
    X_eval = tf.constant(X_arg, dtype = tf.float64, shape=[N,M])
    xn_eval = tf.Variable(tf.zeros([M,1],tf.float64),dtype = tf.float64, shape=[M,1])
 
    # 隠れ層の出力（シグモイド関数）：h = σ(wx + b)の定義　（※データはn個でも1つのyを更新）
    h_eval = tf.Variable(tf.zeros([J,1],tf.float64), dtype = tf.float64, shape=[J,1])    
    # 出力層の出力（ソフトマックス関数）：y = softmax(Wh + b)の定義　（※データはn個でも1つのyを更新）
    y_eval = tf.Variable(tf.zeros([K,1],tf.float64), dtype = tf.float64, shape=[K,1]) 
    # 出力層の結果格納用（正解率「Accuracy」算出に使用）
    yn = tf.Variable(tf.zeros([N,K],tf.float32), dtype = tf.float32, shape=[N,K])   
    # 出力層の正解値tの定義
    t = tf.Variable(t_arg, dtype = tf.float64, shape=[N,K])

    for n in range(N):
        # データをシャッフル
        #X_,t_ = shuffle(X.numpy(),t.numpy())
        X_,t_ = X_eval.numpy(),t.numpy()
        # 取り出したX_[n]を転置してxnに格納(Mx1)
        xn_eval.assign(tf.transpose([X_[n]]))

        # 隠れ層の出力（シグモイド関数）：h = σ(wx + b)の計算
        # 　h[J,1] = sigmoid( W[J×M] × X[M×1] + b[J×1] )
        h_eval.assign( tf.reshape( tf.nn.sigmoid(tf.reshape(tf.matmul(W_arg,xn_eval)+b_arg,[J])),[J,1]).numpy() )
        # 出力層（シグモイド関数）：y = σ(Wx + b)の計算
        # 　y[K,1] = sigmoid( V[K×J] × h[J×1] + c[K×1] )
        y_eval.assign( tf.reshape( tf.nn.sigmoid(tf.reshape(tf.matmul(V_arg,h_eval)+c_arg,[K])),[K,1]).numpy() )
        # 出力yを出力結果保存ynに追加
        yfinal = tf.cast(tf.greater(y_eval,0.5),tf.float32)
        yn[n].assign(tf.reshape(yfinal,[K]))

    ### 評価
    # tとyのマトリックス単位で比較し、正解率（Accuracy）を算出
    m = tf.keras.metrics.Accuracy()
    m.update_state(t,yn)

    ### 評価結果出力
    decimals = 4
    #print("### yn=",np.array_repr(np.round(yn.numpy(),decimals)).replace('\n', '').replace(' ', ''))
    #print("### tn=",np.array_repr(np.round(t.numpy(),decimals)).replace('\n', '').replace(' ', ''))
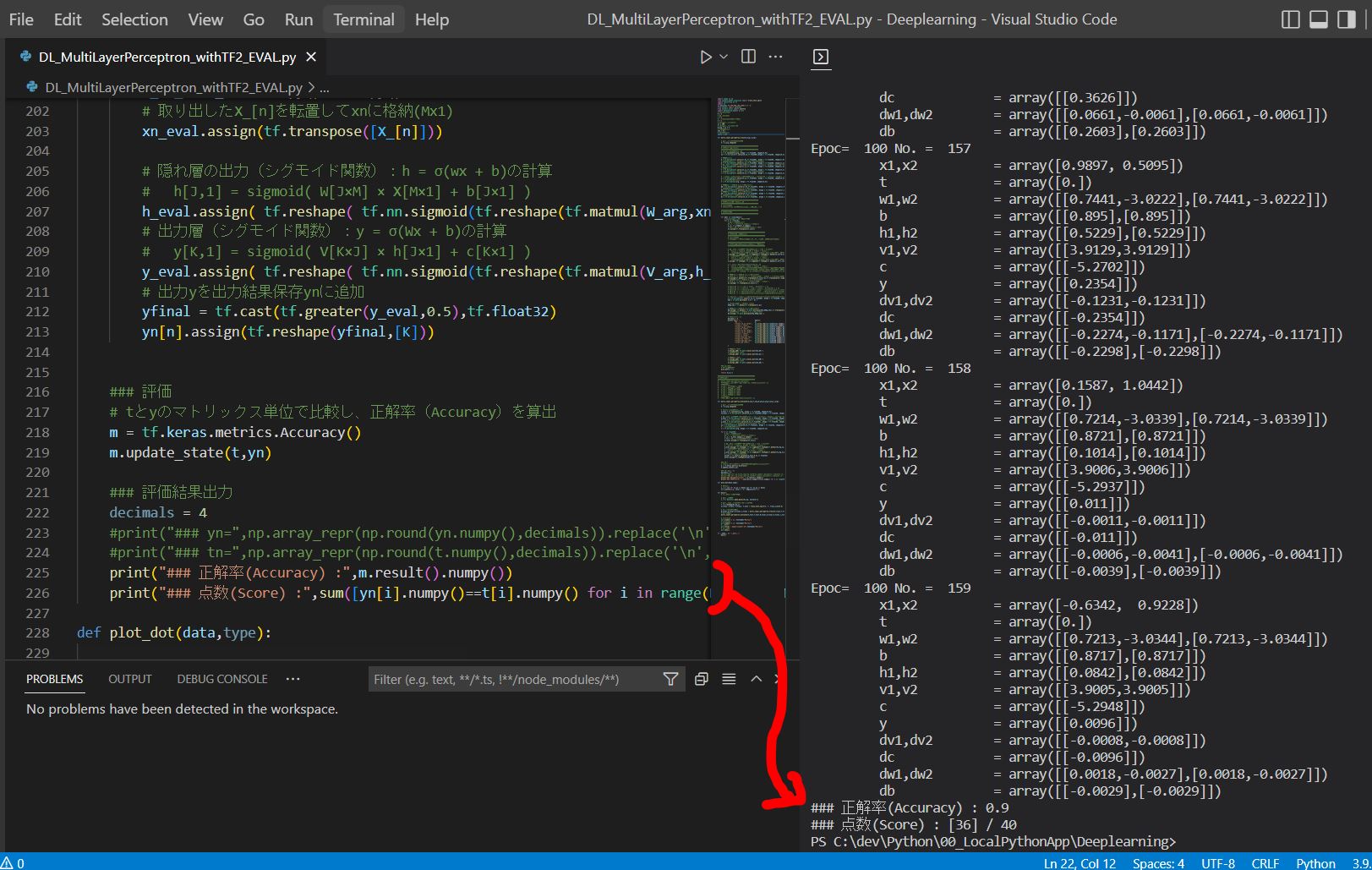
    print("### 正解率(Accuracy) :",m.result().numpy())
    print("### 点数(Score) :",sum([yn[i].numpy()==t[i].numpy() for i in range(N)]),"/",N)

（出力結果）

～略～
Epoc=  100 No. =  158 
         x1,x2          = array([0.1587, 1.0442])
         t              = array([0.])
         w1,w2          = array([[0.7214,-3.0339],[0.7214,-3.0339]])
         b              = array([[0.8721],[0.8721]])
         h1,h2          = array([[0.1014],[0.1014]])
         v1,v2          = array([[3.9006,3.9006]])
         c              = array([[-5.2937]])
         y              = array([[0.011]])
         dv1,dv2        = array([[-0.0011,-0.0011]])
         dc             = array([[-0.011]]) 
         dw1,dw2        = array([[-0.0006,-0.0041],[-0.0006,-0.0041]])
         db             = array([[-0.0039],[-0.0039]])
Epoc=  100 No. =  159 
         x1,x2          = array([-0.6342,  0.9228])
         t              = array([0.])
         w1,w2          = array([[0.7213,-3.0344],[0.7213,-3.0344]])
         b              = array([[0.8717],[0.8717]])
         h1,h2          = array([[0.0842],[0.0842]])
         v1,v2          = array([[3.9005,3.9005]])
         c              = array([[-5.2948]])
         y              = array([[0.0096]])
         dv1,dv2        = array([[-0.0008,-0.0008]])
         dc             = array([[-0.0096]])
         dw1,dw2        = array([[0.0018,-0.0027],[0.0018,-0.0027]])
         db             = array([[-0.0029],[-0.0029]])
### 正解率(Accuracy) : 0.9
### 点数(Score) : [36] / 40

（図１４１）

＞目次にもどる

(１-４) モデルの評価の実装例②（Keras）

Kerasでは、以下のように簡単に評価を行うことが可能です。

●評価の方法

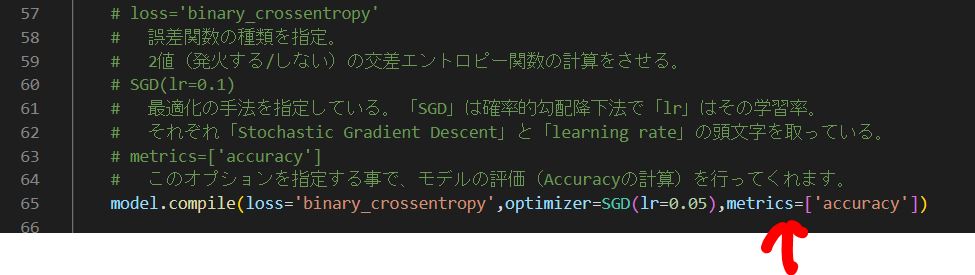
モデルのコンパイル時に metrics='accuracy' を指定（Keras公式ドキュメント）

model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.05), metrics=['accuracy'])

（図１４２①・②）Before→After

↓

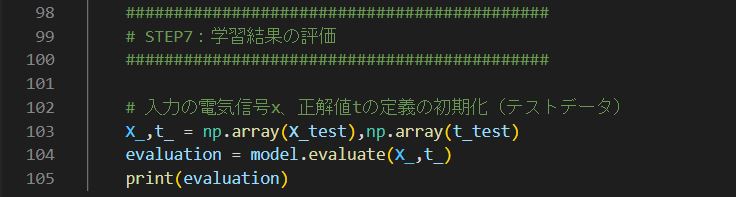
model.evaluate([入力],[正解]) で評価

evaluation = model.evaluate(X_test, t_test)

（図１４３）

以下は全体コード例です：

import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD
from sklearn.model_selection import train_test_split
from sklearn.utils import shuffle
from sklearn import datasets

# 入力xの次元
M = 2
# 隠れ層hの次元（クラス数）
J = 4
# 出力yの次元（クラス数）
K = 1
# 入力データセットの総
nc = 300
# 入力データセットの総数
N = nc * K
# エポック数
epoch_num = 100
# ミニバッチのサイズ
mini_batch_size = 20

def multi_layer_perceptron(X_train,t_train,X_test,t_test):
    ############################################
    # STEP1：モデルの定義
    ############################################

    # 入力の電気信号x、正解値tの定義の初期化（トレーニングデータ）
    X,t = np.array(X_train),np.array(t_train)
    #X_,t_ = shuffle(X,t)

    # 入力層 - 隠れ層の定義
    # 　Dense(input_dim=M, units=J)：入力がM次元、出力がJ次元のネットワーク
    # 　　⇒ W[J行×M列] × xn[M行×1列] + b[J行×1列]に相当
    # 　Activation('sigmoid')：活性化関数として、シグモイド関数を指定
    # 　　⇒ y = σ(wx + b)に相当
    model = Sequential()
    model.add(Dense(input_dim=M, units=J))
    model.add(Activation('sigmoid'))
    
    # 隠れ層 - 出力層の定義
    # 　Dense(units=K)：出力がK次元のネットワーク
    # 　　⇒ V[K行×J列] × h[J行×1列] + c[K行×1列]に相当
    model.add(Dense(units=K))
    model.add(Activation('sigmoid'))

    ############################################
    # STEP2：誤差関数の定義
    ############################################
    # ⇒compile時の引数として「binary_crossentropy」を指定

    ############################################
    # STEP3：最適化手法の定義（例：確率的勾配降下法）
    ############################################

    # loss='binary_crossentropy'
    # 　誤差関数の種類を指定。
    # 　2値（発火する/しない）の交差エントロピー関数の計算をさせる。
    # SGD(lr=0.1)
    # 　最適化の手法を指定している。「SGD」は確率的勾配降下法で「lr」はその学習率。
    # 　それぞれ「Stochastic Gradient Descent」と「learning rate」の頭文字を取っている。
    # metrics=['accuracy']
    # 　このオプションを指定する事で、モデルの評価（Accuracyの計算）を行ってくれます。
    model.compile(loss='binary_crossentropy',optimizer=SGD(lr=0.05),metrics=['accuracy'])

    ############################################
    # STEP4：セッションの初期化
    ############################################
    # ⇒今回は不要
    # （TensorFlow v2以降はSessionを使用しないため）

    ############################################
    # STEP5：学習
    ############################################

    # 指定したエポック数、繰り返し学習を行う
    # 　第1引数：Xは入力データ（入力の電気信号）
    # 　第2引数：tは正解データ（出力の電気信号の正解値）
    # 　第3引数：エポック（データ全体に対する反復回数）の数
    # 　第4引数：ミニバッチ勾配降下法（N個の入力データをM個ずつのグループに分けて学習する際のMの値）
    model.fit(X, t, epochs=epoch_num, batch_size=mini_batch_size)

    ############################################
    # STEP6：学習結果の確認
    ############################################

    # 分類が正しい結果になっているか？（発火するかどうか？が正しい結果になっているか）
    classes = (model.predict(X,batch_size=mini_batch_size) > 0.5).astype("int32")
    # ネットワークの出力「y」の計算結果を取得
    prob = model.predict(X,batch_size=mini_batch_size)

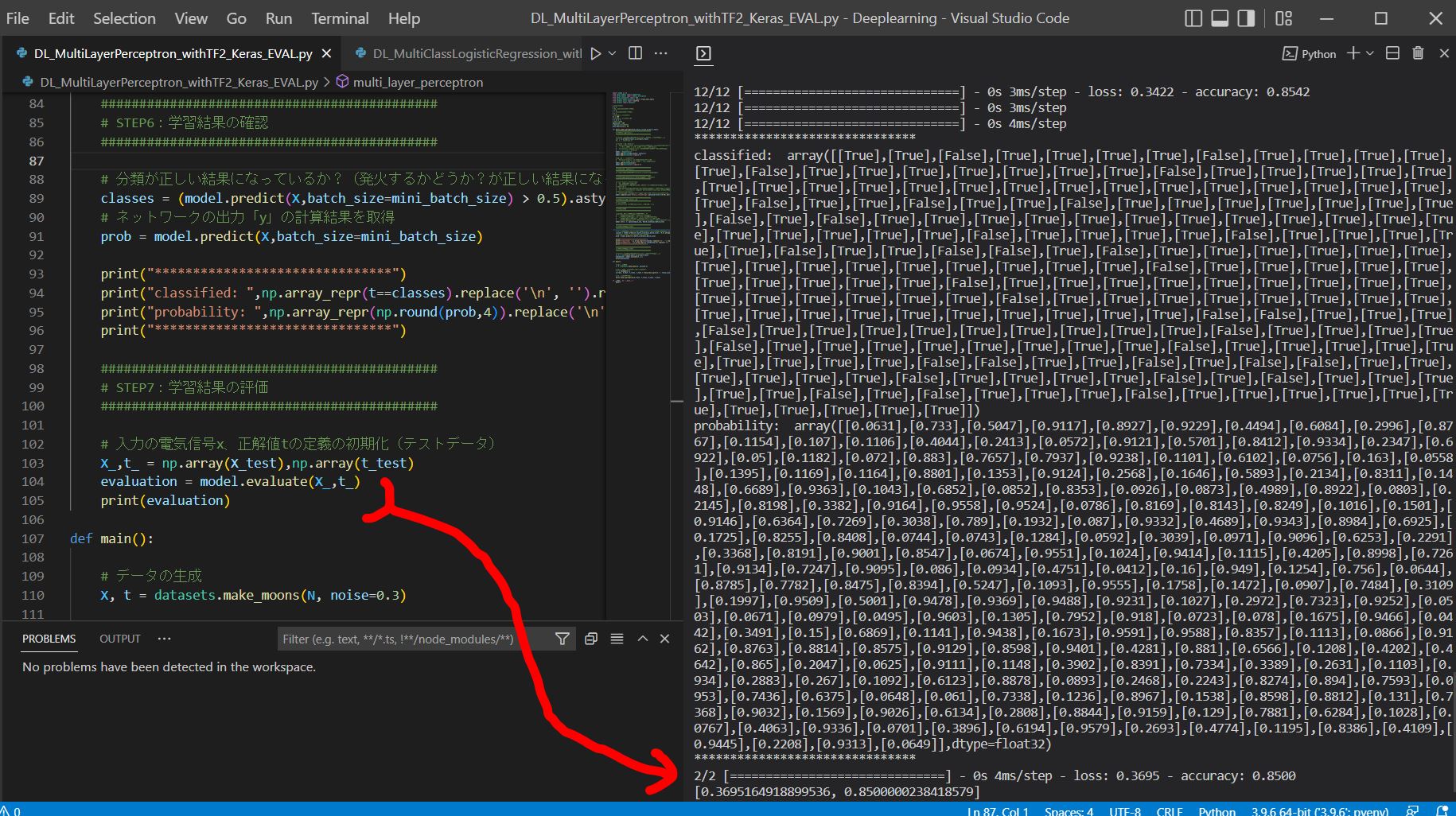
    print("*******************************")
    print("classified: ",np.array_repr(t==classes).replace('\n', '').replace(' ', ''))
    print("probability: ",np.array_repr(np.round(prob,4)).replace('\n', '').replace(' ', ''))
    print("*******************************")

    ############################################
    # STEP7：学習結果の評価
    ############################################

    # 入力の電気信号x、正解値tの定義の初期化（テストデータ）
    X_,t_ = np.array(X_test),np.array(t_test)
    evaluation = model.evaluate(X_,t_)
    print(evaluation)

def main():

    # データの生成
    X, t = datasets.make_moons(N, noise=0.3)
    
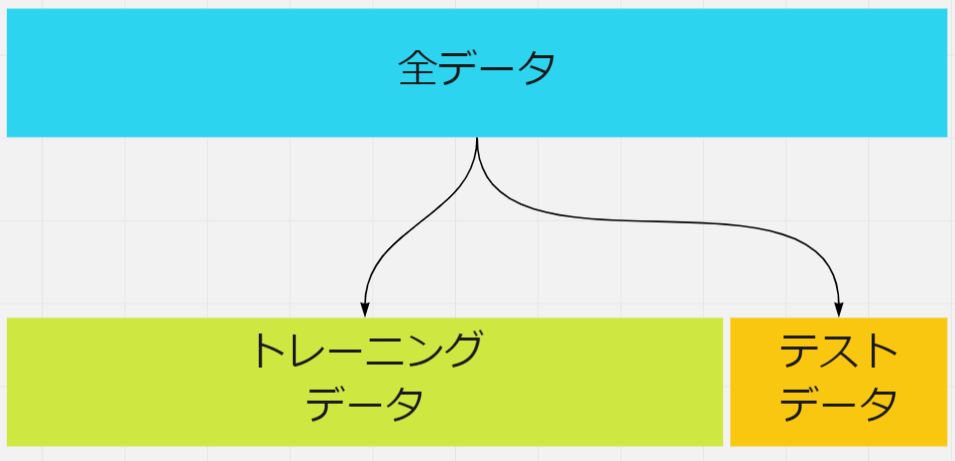
    # データをトレーニング用/評価用とに分類
    T = t.reshape(N,1)
    X_train, X_test, T_train, T_test = train_test_split(X, T, train_size=0.8)

    # トレーニング＆評価
    multi_layer_perceptron(X_train, T_train, X_test, T_test)
  
if __name__ == "__main__":
    main()

（図１４４）

＞目次にもどる