＜目次＞
(１) int型のオーバーフロー（桁あふれ）とは？実際の発生パターンと併せてご紹介
(１-１) int型のオーバーフローとは？
(１-２) int型のオーバーフローが発生するとどうなるの？
(１-３) int型のオーバーフローの発生サンプル
(１) int型のオーバーフロー（桁あふれ）とは？実際の発生パターンと併せてご紹介
(１-１) int型のオーバーフローとは？
int型のオーバーフロー（桁あふれ）とは、int型の変数にintで保持できる最大値（符号付き32bitの場合、+2,147,483,647～-2,147,483,648の範囲）を超える値を格納しようとした際に発生します。
多くのプログラミング言語において、通常int型の値には決められたビット数のメモリが割り当てられます。例えば、32bitのinteger型が確保した猟奇の場合、次の範囲の数値を保持できます。
・符号あり32bit（int）
| ■10進数 | ■2進数 | ■16進数 |
| 2,147,483,647 = pow(2,31) – 1 |
01111111 11111111 11111111 11111111 | 0x7FFFFFFF |
| -2,147,483,648 = pow(2,31) |
10000000 00000000 00000000 00000000 | 0x80000000 |
・符号なし32bit（unsigned int）
| ■10進数 | ■2進数 | ■16進数 |
| 0 = pow(2,0) – 1 |
00000000 00000000 00000000 00000000 | 0x00000000 |
| 4,294,967,295 = pow(2,32) -1 |
11111111 11111111 11111111 11111111 | 0xFFFFFFFF |
(１-２) int型のオーバーフローが発生するとどうなるの？
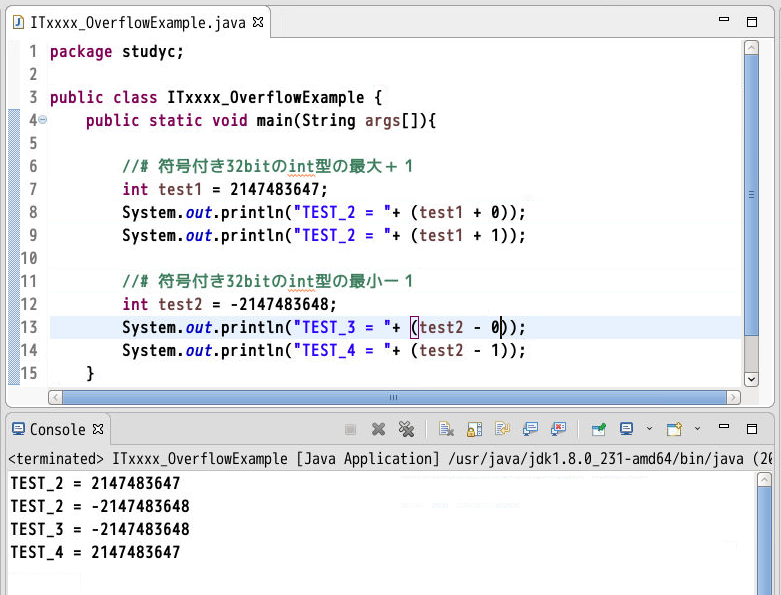
以下はJavaの例ですが、両端（最大=2147483647と最小=-2147483648）の数字に対して、最大は更に+1、最小は更に-1するとどうなるか？をチェックしていますが、結果的には逆側の最大値に反転しています。
・MAX+1 = 2147483647+1 = －2147483648
・MIN－1 = －2147483648－1 = 2147483647
public class ITxxxx_OverflowExample {
public static void main(String args[]){
//# 符号付き32bitのint型の最大＋１
int test1 = 2147483647;
System.out.println("TEST_1 = "+ (test1 + 0));
System.out.println("TEST_2 = "+ (test1 + 1));
//# 符号付き32bitのint型の最小ー１
int test2 = -2147483648;
System.out.println("TEST_3 = "+ (test2 - 0));
System.out.println("TEST_4 = "+ (test2 - 1));
}
}
（図１２１）
この結果として、オーバーフローにより意図せず符号が反転してしまい、配列などでマイナスのインデックスが指定されてしまい、「ArrayIndexOutOfBoundsException」等の例外につながる、といった問題が想定されます。
また、この例はJavaですが他にもC#やC++など多くのプログラミング言語では同様の挙動をしています（Python等の例外もあり）。
(１-３) int型のオーバーフローの発生サンプル
実際に数値解析等のアルゴリズムにおいても、オーバーフローが発生する可能性があります。
（例）バイナリサーチ
こちらのバイナリサーチの紹介記事に掲載しているプログラムですが、範囲の中央（mid）を求める所で次のように記載しています。
//① int mid = (lo + hi) / 2;
一見すると問題ないように見えますが、この計算は探索対象の配列が非常に大きい場合に「lo + hi」が「int型の最大」である「2147483647」を超えた場合にオーバーフローが発生する可能性があるため、正しくは次のように記載する必要があります。
//② int mid = lo + (hi – lo) / 2;
この②は一見すると①と別の式に見えますが、実際に式変換すると同じ式である事が分かります。
② = lo + (hi – lo) / 2 = (2*lo + (hi – lo)) / 2 = (lo + hi) / 2 = ①
