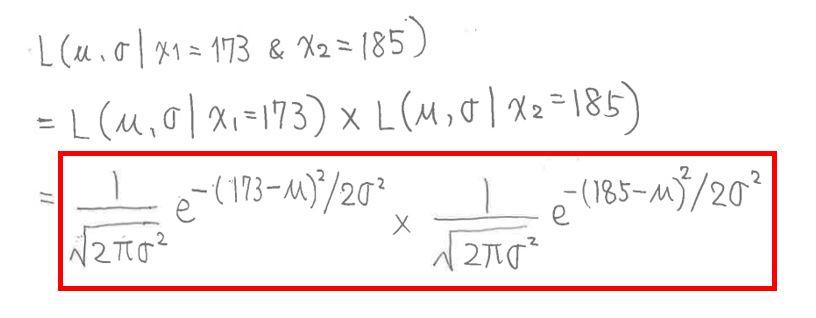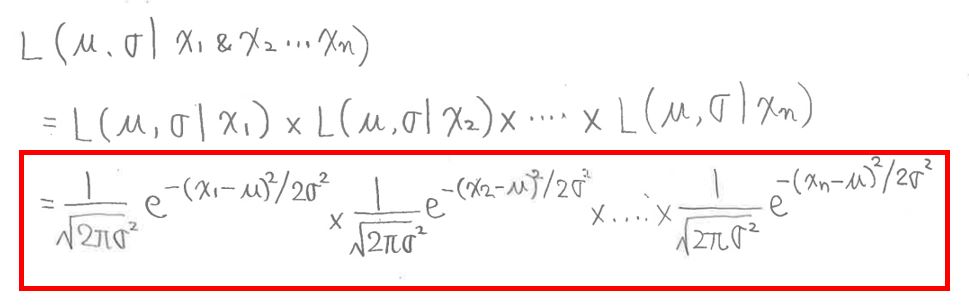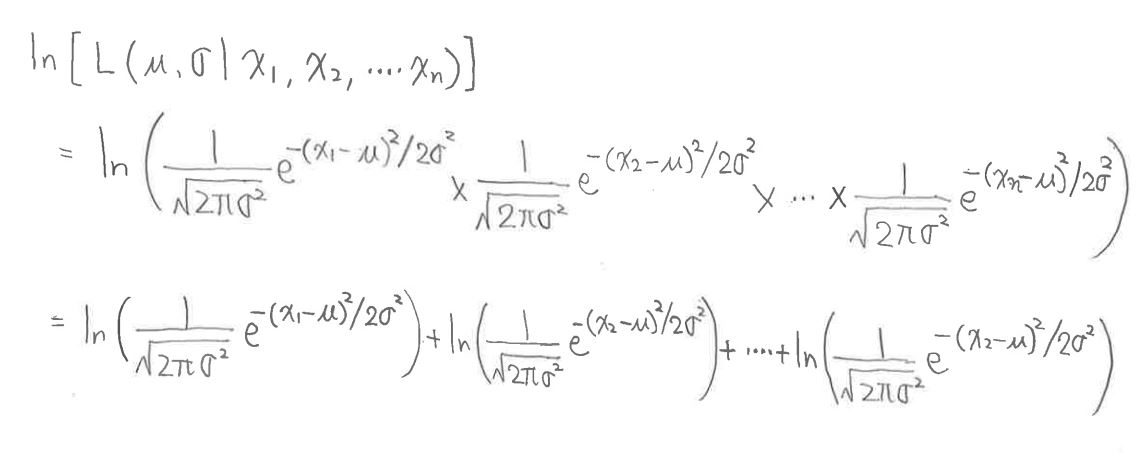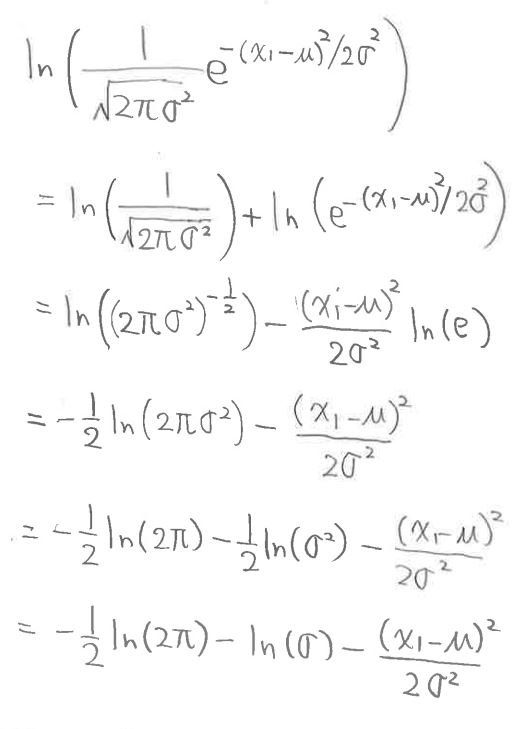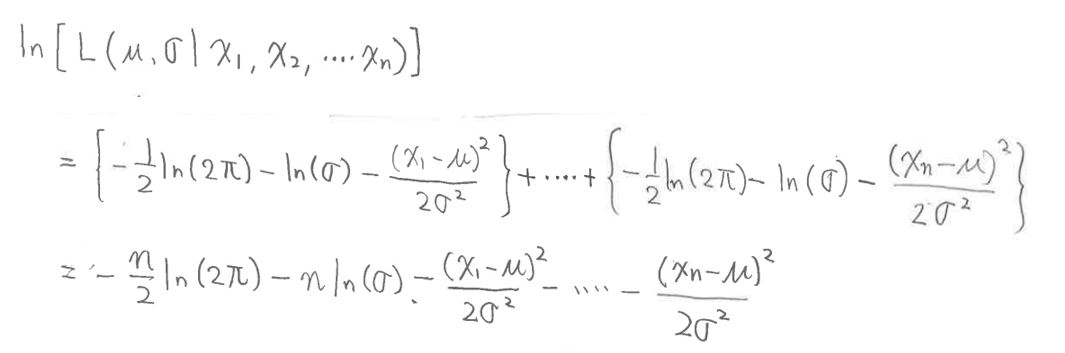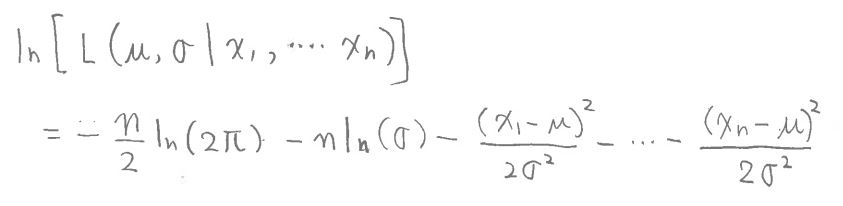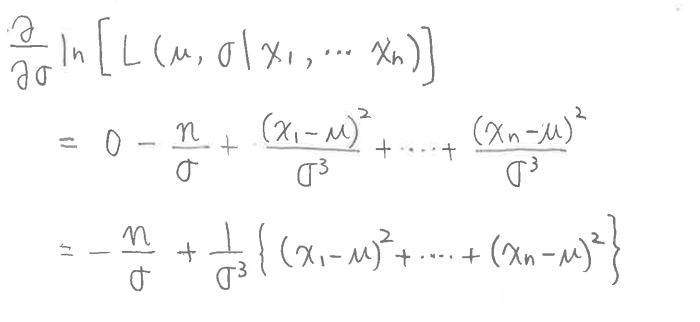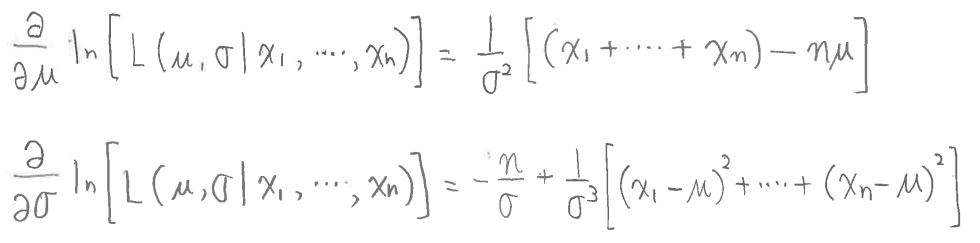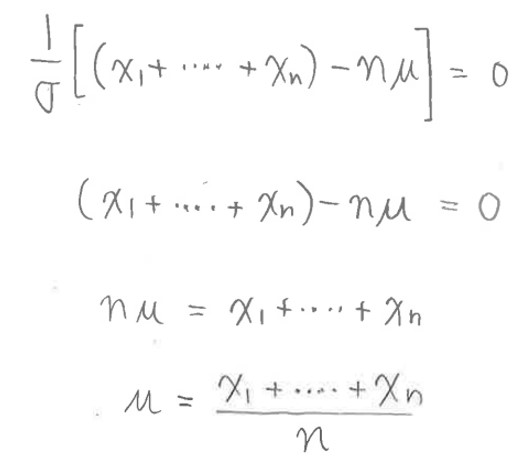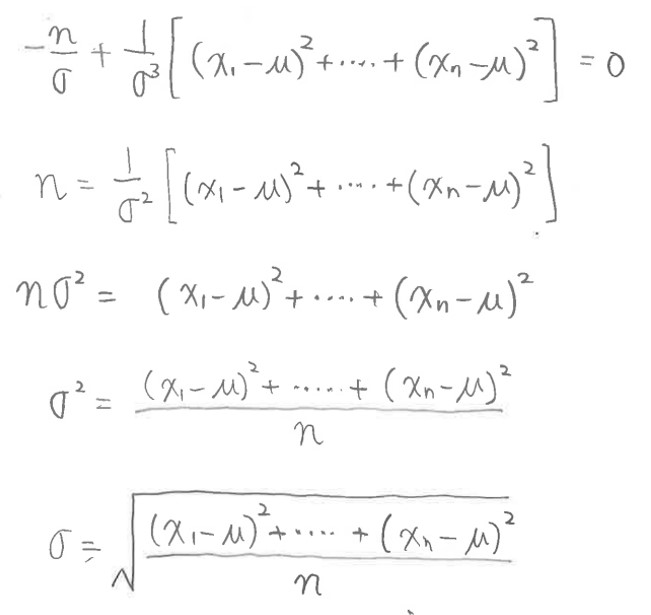<目次>
(1) 最尤推定の計算を正規分布で行った例をご紹介
(1-1) 最尤推定とは?
(1-2) 最尤推定の計算の流れ
(1-3) STEP1:分布の種類を仮定(例:正規分布、シグモイド関数)
(1-4) STEP2:尤度関数を設定
(1-5) STEP3:片方のパラメータ(標準偏差σ)を固定して「平均値μ」を推定
(1-6) STEP4:もう片方のパラメータ(平均値μ)を固定して「標準偏差σ」を推定
(1-7) STEP5:尤度関数の最大値(=傾き0=偏微分が0)を求める
(1) 最尤推定の計算を正規分布で行った例をご紹介
本記事では「正規分布」を使って、最尤推定の計算をご紹介します。
(1-1) 最尤推定とは?
最尤推定の概要や考え方については、下記をご参照ください。
⇒(前提①)最尤推定とは?ディープラーニングでの使われ方と絡めてシンプルに解説
⇒(前提②)確率と尤度の違いとは?概念や数式なども交えて比較紹介
(1-2) 最尤推定の計算の流れ
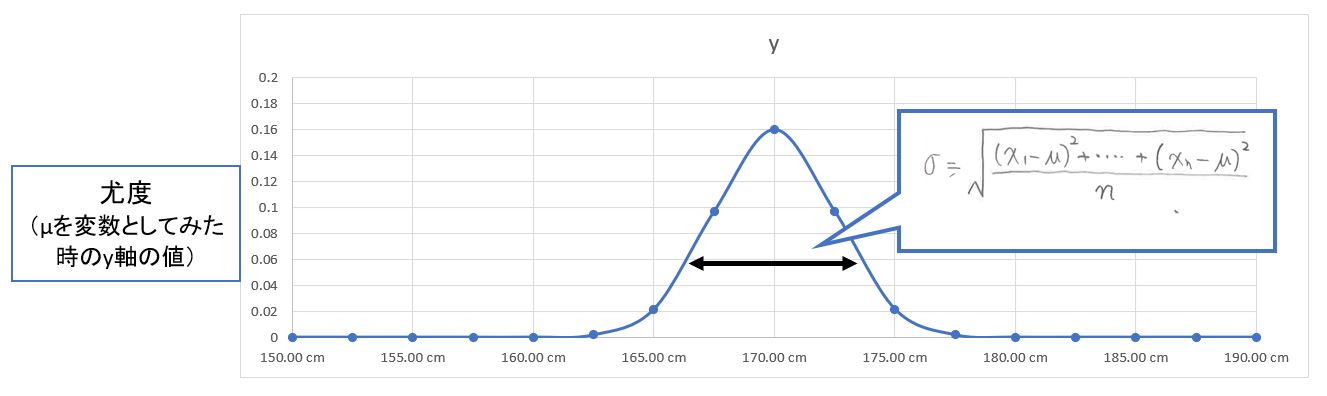
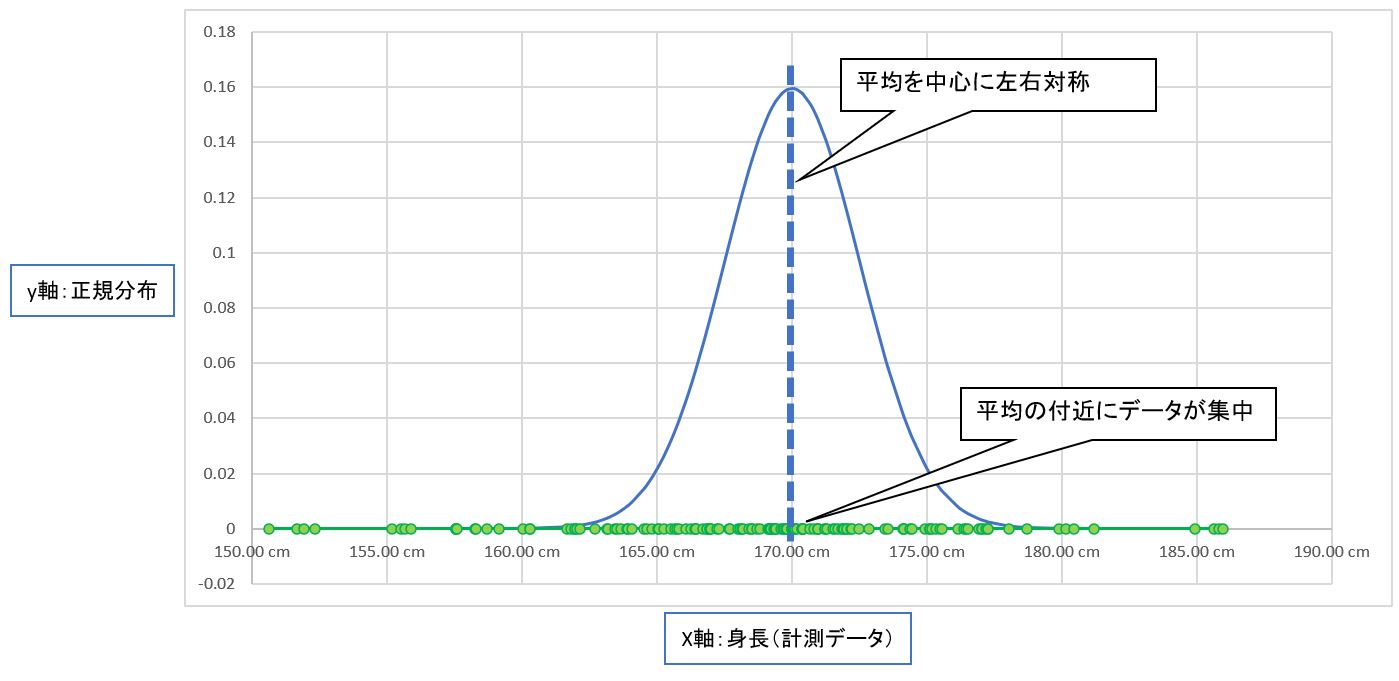
今回は例として「小学生の身長」の「正規分布」のパラメータ(平均値μ、標準偏差σ)を、実際の測定データX(200人の身長データ)から「最尤推定」を行うと想定します。
(図111)
(1-3) STEP1:分布の種類を仮定(例:正規分布、シグモイド関数)
今回の例では、分布の種類は「正規分布」なので、まずはその基本性質を簡単に紹介します。
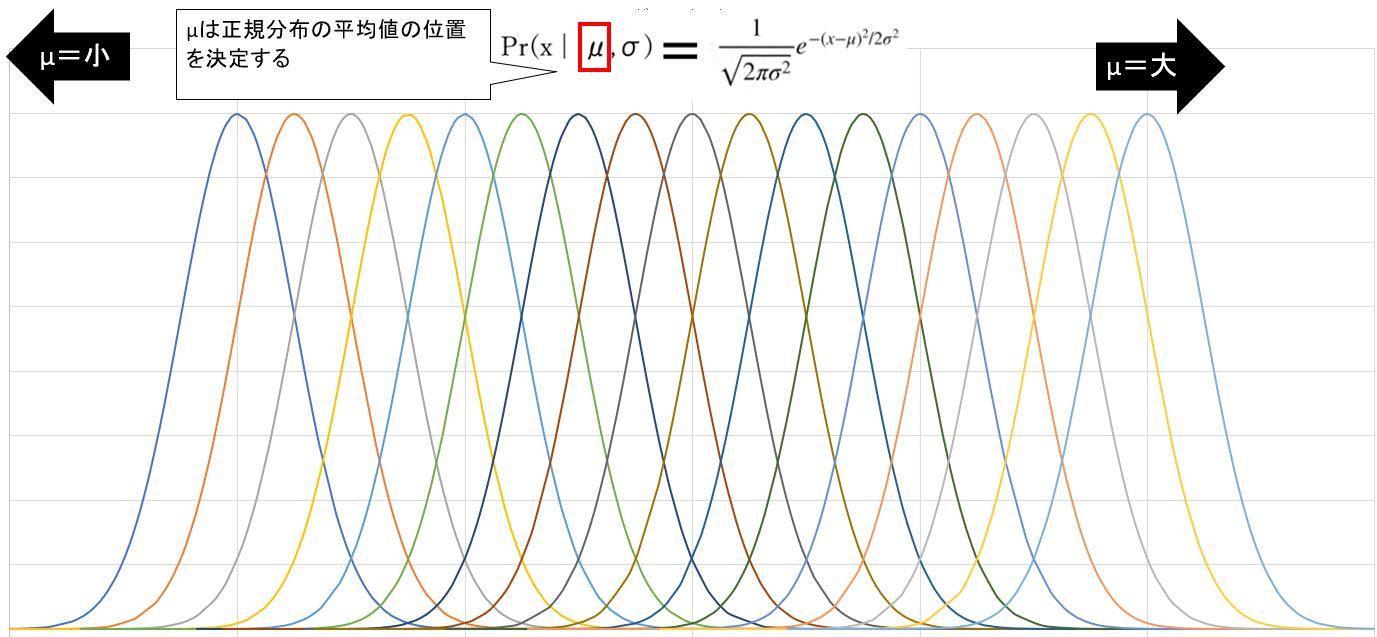
●①正規分布の計算式を理解:μ(ミュー)
μ(ミュー)=平均(mean)は正規分布の平均値の事。
⇒値が小さければグラフは左に、値が大きければグラフは右にシフトします。
(図121①)
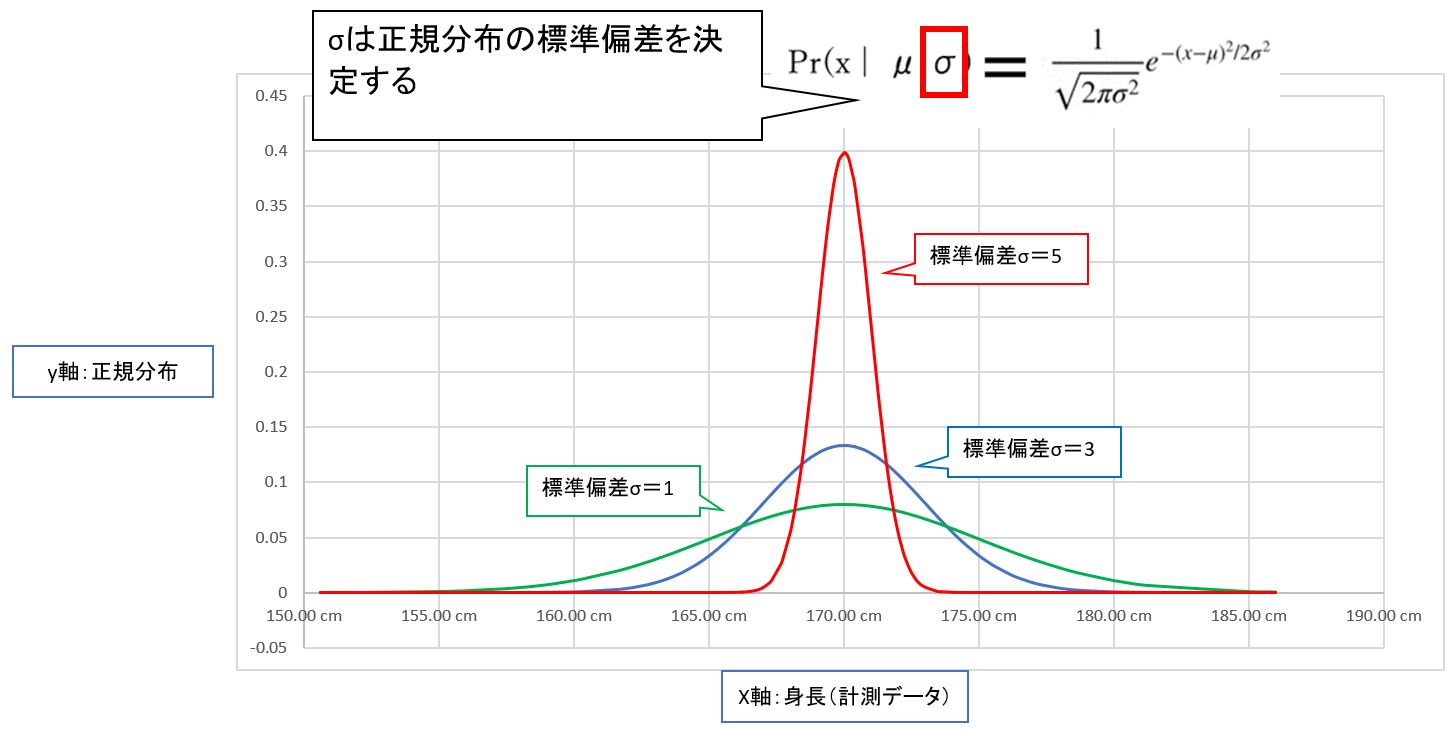
●②正規分布の計算式を理解:σ(シグマ)
σ(シグマ)=標準偏差(standard deviation)は正規分布の「水平方向の幅」を表す。
⇒値が小さければ「細く高く」、値が大きければ「太く低く」なります。
(図122)
(1-4) STEP2:尤度関数を設定
(1-4-1) STEP2-1:単一データの尤度関数
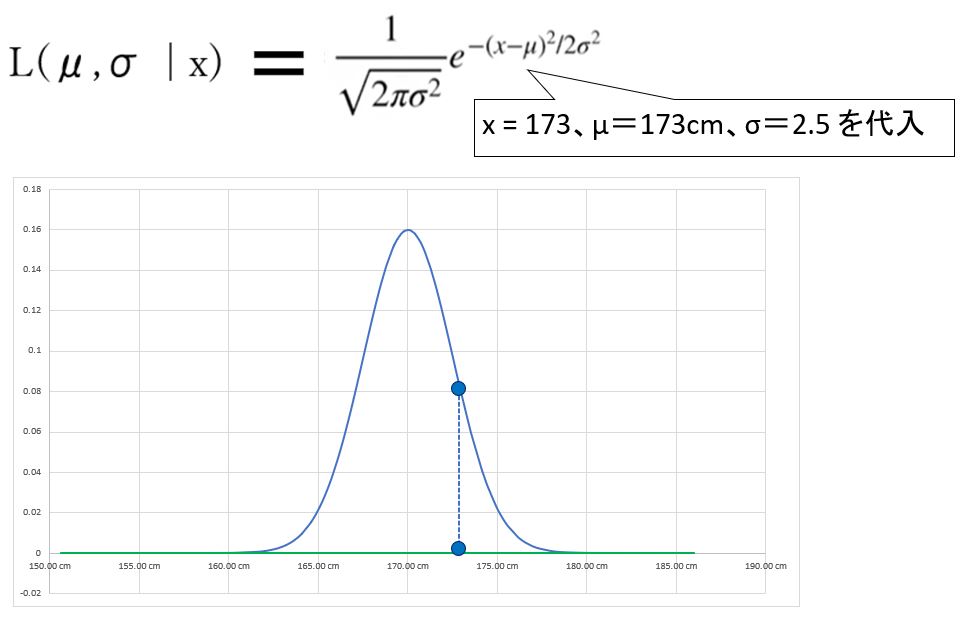
まずは「身長x1=173cm」の単一の計測データOがあるケースを考えます。
尤度を求めるための「
尤度関数」は下記の式で表現できます。
L(μ,σ | x1=173) = Pr(x1=173 | μ,σ)
このとき「P(x1=173 | μ,σ)」は
確率密度関数です。
正規分布の場合、以下のような式になります。
(図123)
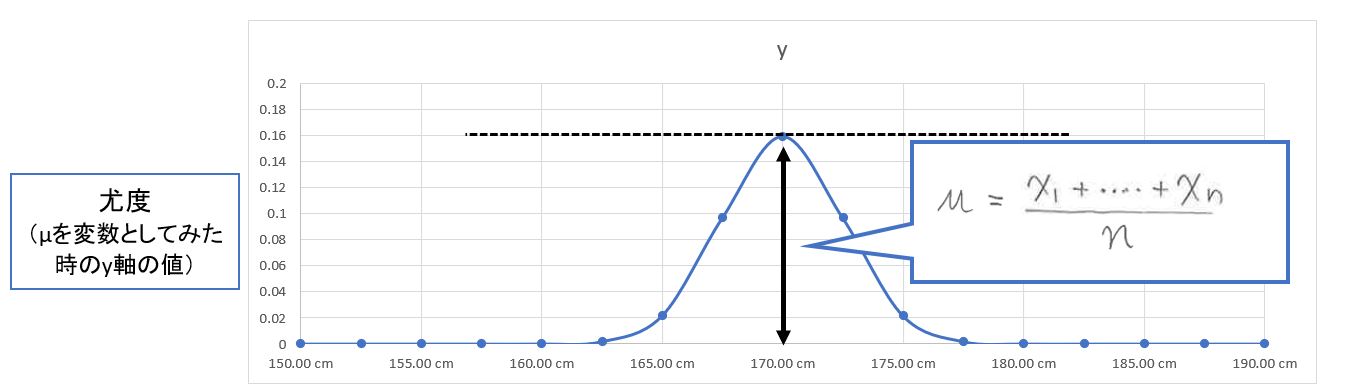
「尤度」はデータO(身長x1=173cm)とパラメータ(例:平均値μ=173cm、標準偏差σ=2.5)を尤度関数に代入すれば求まります。
(図124)
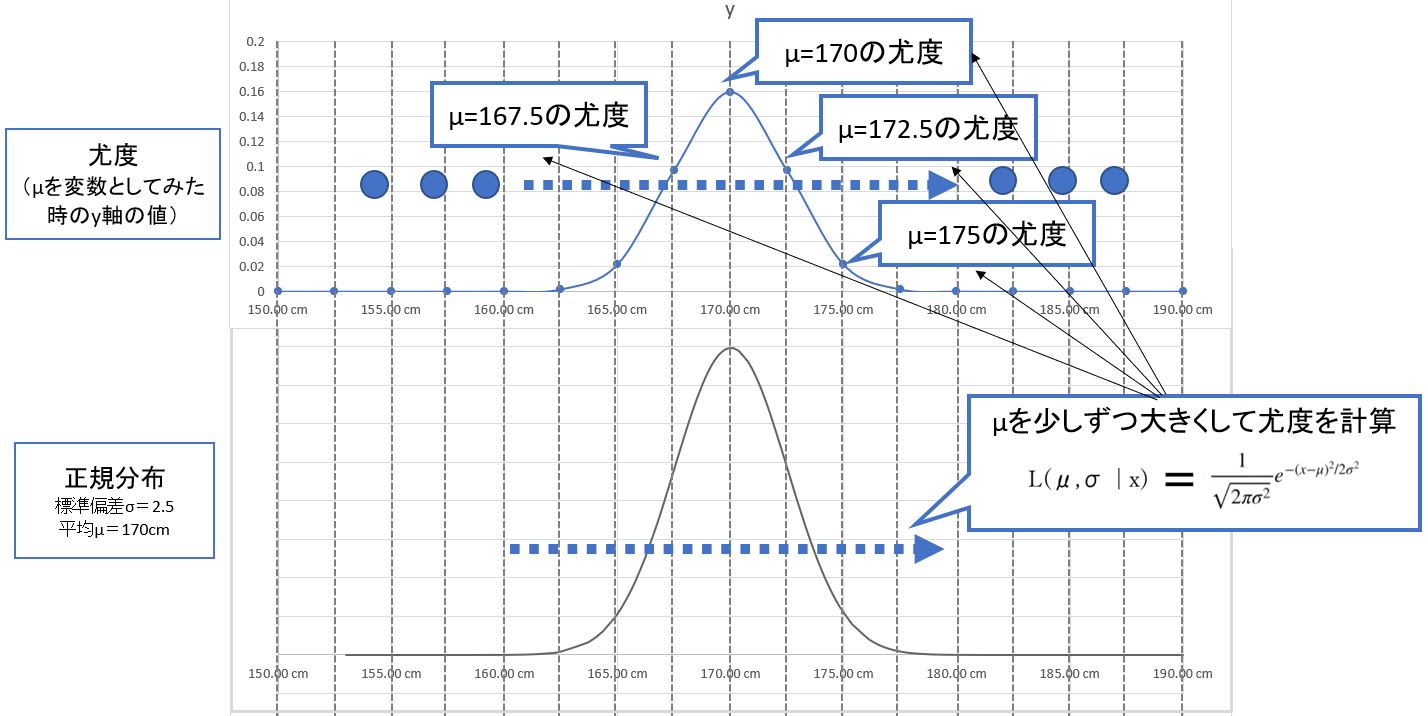
・μの最尤推定では、σを固定&μを少しずつシフトして「μの尤度」を再計算し、尤度が最大となるμを見つけます。そのμが分布の「尤もらしい」平均値です。
・σについても同様に、μを固定&σを少しずつシフトして「σの尤度」を再計算し、尤度が最大となるσ見つけます。
(図125)
(注意)
・上記はイメージを掴むための説明で、実際に最尤推定する時は逐一シフト&再計算はしません。
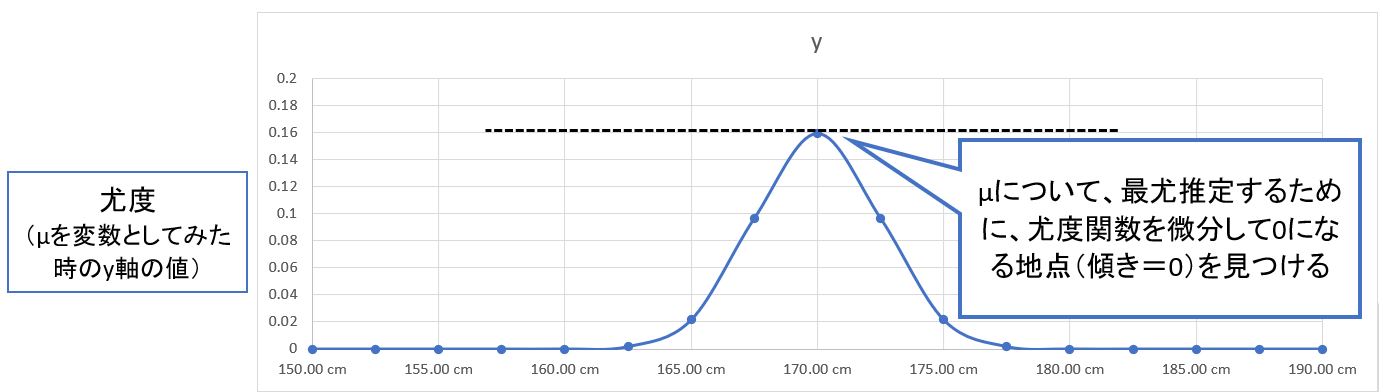
・実際は、尤度関数をμについて偏微分した式(傾き)が0になる(最大となる)μの値を求めます。
(1-4-2) STEP2-2:複数データの尤度関数
次に測定データが複数の場合(例:身長x1=173cm、x2=185cm)を考えます。
尤度を求めるための「
尤度関数」は下記のように表せます。
L(μ,σ | x1 & x2) = Pr(x1 & x2 | μ,σ)
測定結果x1とx2は独立である(お互いに影響しない)事から、それぞれの尤度関数の「積」で表現できます。
L(μ,σ | x1=173 & x2=185)
= L(μ,σ | x1=173) × L(μ,σ | x2=185)
(図126①)
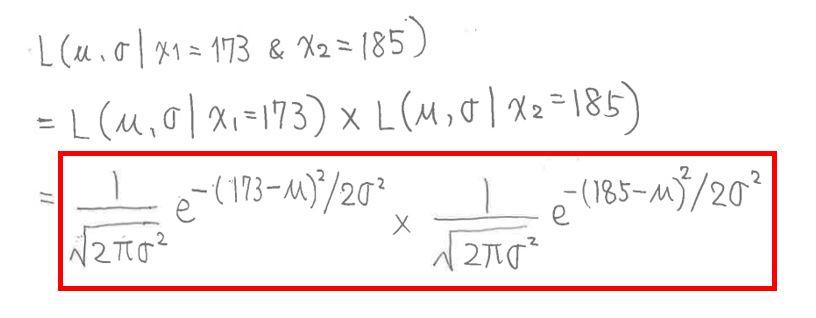
データの数がn個の場合でも同様に考える事ができます。
L(μ,σ | x1 & x2 & … & xn)
= L(μ,σ | x1) × L(μ,σ | x2) ×…× L(μ,σ | xn)
(図126②)
これで正規分布の尤度の計算(複数の入力データOがある場合)が分かったので、ここからは「標準偏差σ」と「平均値μ」について最尤推定をしていきます。
(1-5) STEP3:片方のパラメータ(標準偏差σ)を固定して「平均値μ」を推定
(1-5-0) 方針とポイント
(方針)
尤度関数をμについて偏微分した式(傾き)が0になる(最大となる)μの値を求めます。
(図126③)
(ポイント)
この時、両辺の「対数」をとります。理由は、対数をとる事で微分の計算が簡単になるためです。
(図127①)
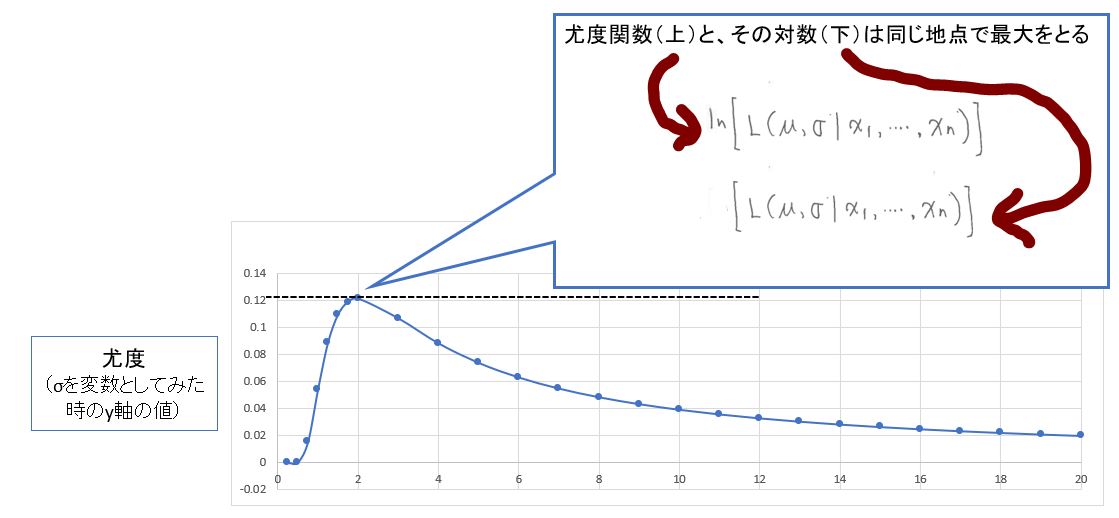
加えて「尤度関数」と「尤度関数のlog」は、共に同じ地点で傾きが最大になる(σとμの両方とも)ので、対数をとって計算を進めます。
(図127②)
(1-5-1) STEP3-1:対数をとる
・尤度関数のlogをとったものを式変形していきます。
(図127③)
↓
・n個の和のうちx1の項に着目して部分的に式変形
(図127④)
↓
・これを元の式に代入して計算すると・・
(図127⑤)
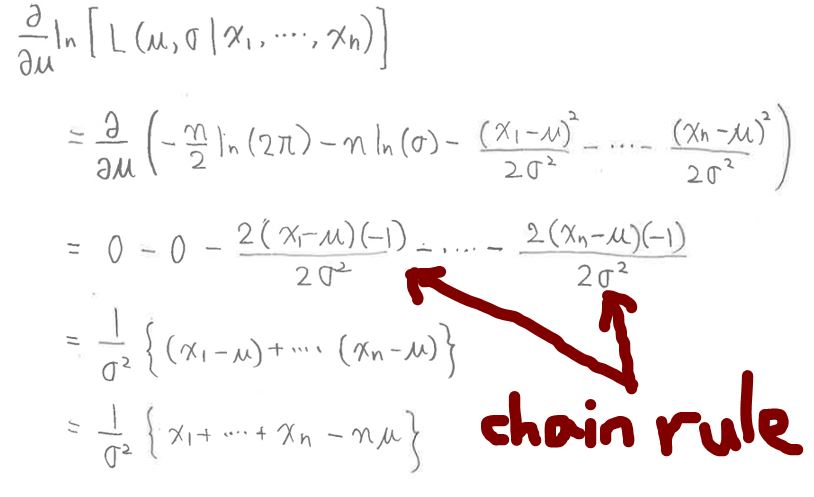
(1-5-2) STEP3-2:微分をする
・式変形の途中で連鎖率(chain rule)を使って変形
(図128①)
(1-6) STEP4:もう片方のパラメータ(平均値μ)を固定して「標準偏差σ」を推定
(1-6-0) 方針とポイント
(方針)
尤度関数をσについて偏微分した式(傾き)が0になる(最大となる)σの値を求めます。
(図131①)
(ポイント)
μの時と同様、両辺の「対数」をとり、微分の計算を行います。
(1-6-1) STEP4-1:対数をとる
・尤度関数のlogをとったものを式変形していきます。
(図131②)
(1-6-2) STEP4-2:微分をする
(図131③)
(1-7) STEP5:尤度関数の最大値(=傾き0=偏微分が0)を求める
μとσのそれぞれの尤度関数の偏微分の式。
(図141①)
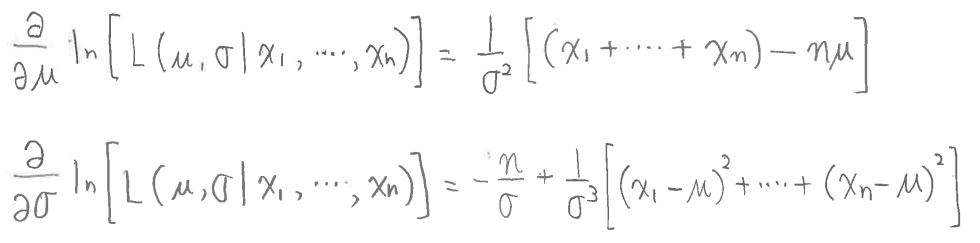
これを、μとσのそれぞれについて解きます。
(1-7-1) 平均値μについて解く
(図142①)
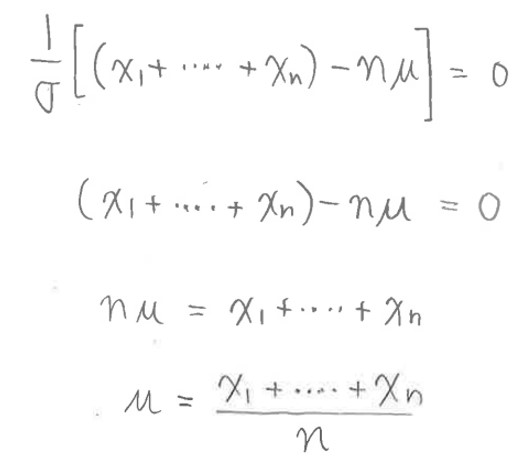
(図142②)μは正規分布の平均(中央)のy軸値になる
(1-7-2) 標準偏差σについて解く
(図143①)
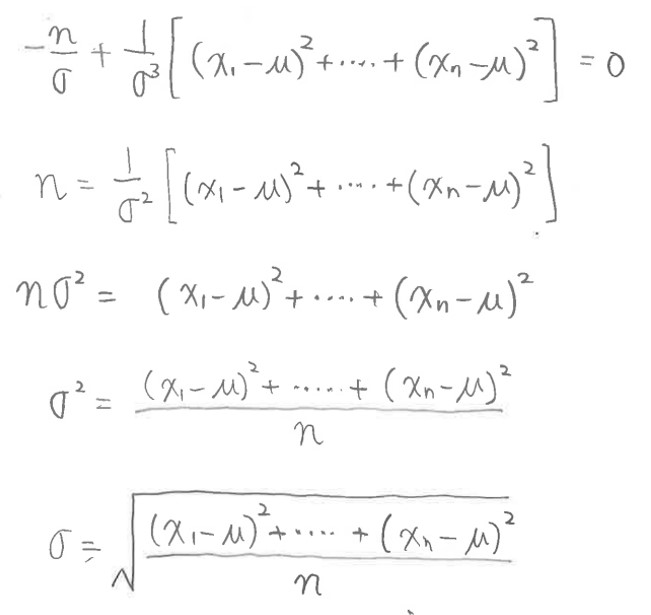
(図143②)σは正規分布の幅を決める値