<目次>
ロジスティック回帰の式変形(多クラス版)のご紹介(ディープラーニング)
【前提】多クラスロジスティック回帰とは?
【本編】多クラスロジスティック回帰の流れを整理
STEP1:分布の種類を仮定(シグモイド関数)【Excel】
STEP2:尤度関数を設定
STEP3:片方パラメータ(重みw)を固定して「バイアスb」を推定
STEP4:もう片方のパラメータ(バイアスb)を固定して「重みw」を推定
STEP5:尤度関数の最大値(=傾き0=偏微分が0)を求める【Excel】
【オマケ】多クラスのロジスティック回帰をExcelで計算
ロジスティック回帰の式変形(多クラス版)のご紹介(ディープラーニング)
【前提】多クラスロジスティック回帰とは?
・ニューラルネットワークのモデルの種類の1つで、活性化関数として「ソフトマックス関数」を採用しているのが特徴です。
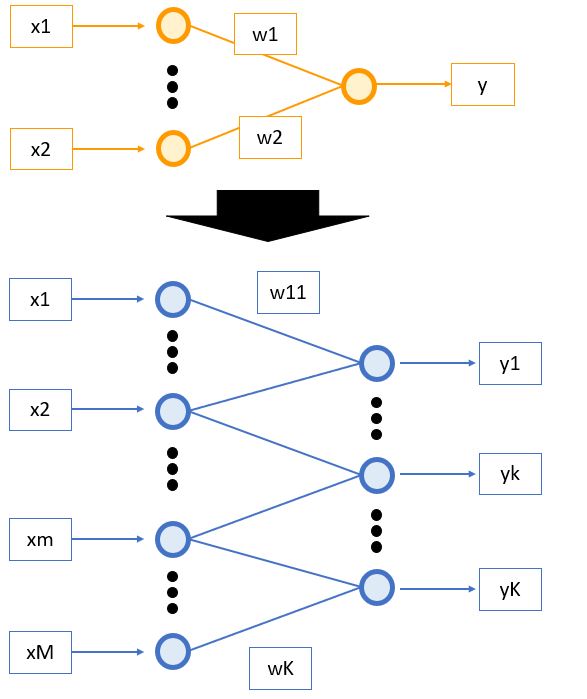
(図100)2値分類 ⇒ 多クラス分類へ
・「シグモイド関数」を用いた
ロジスティック回帰は「発火するorしない」の2値分類(例:迷惑メールである/でない)であるのに対し、「ソフトマックス関数」を使う事で多クラス(3クラス以上)を表現できます。
・例えば、「犬/猫/ハムスター/ウサギ」や「晴/曇/雨/雷/雪」などが多クラスの例です。
●多クラスロジスティック回帰モデルの出力式
\( \boldsymbol{y} = f(\boldsymbol{W} \boldsymbol{x} + \boldsymbol{b}) \)
この時活性化関数\( f( \cdot ) \)はソフトマックス関数で、\( y, W, b \)はそれぞれ以下の通り。
\( \boldsymbol{y} = \begin{pmatrix} y_1 \\ \vdots \\ y_k \\ \vdots \\ y_{K} \end{pmatrix} \)
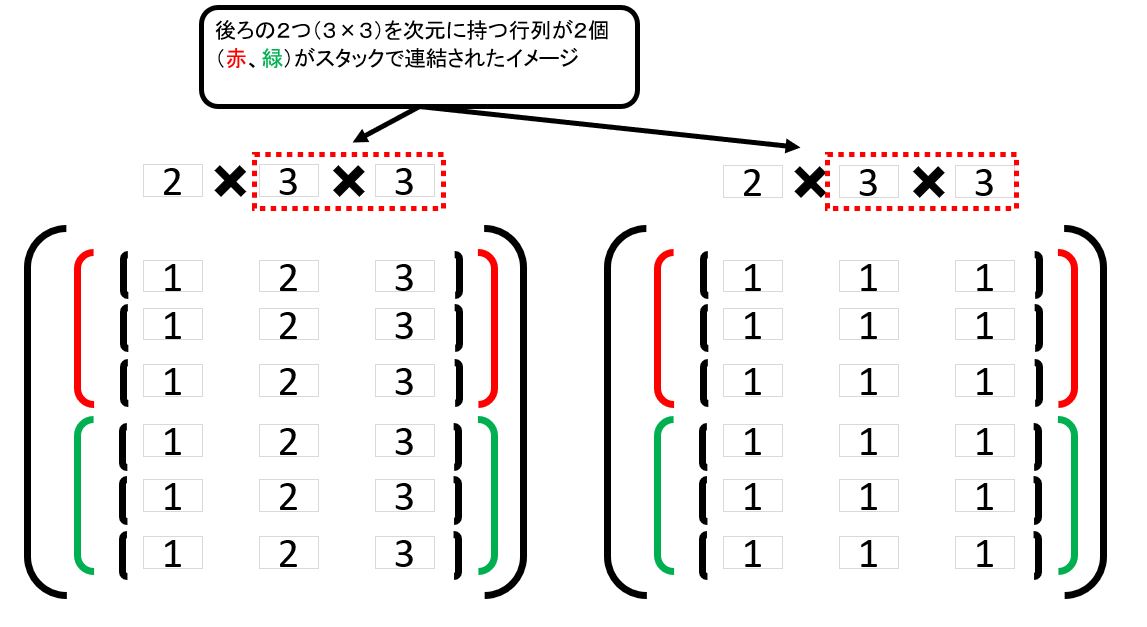
\( \boldsymbol{W} = \begin{pmatrix} w_{11} & \cdots & w_{1m} & \cdots & w_{1M} \\ \vdots \\ w_{k1} & \cdots & w_{km} & \cdots & w_{kM} \\ \vdots \\ w_{K1} & \cdots & w_{Km} & \cdots & w_{KM} \end{pmatrix} \)
\( \boldsymbol{b} = \begin{pmatrix} b_1 \\ \vdots \\ b_k \\ \vdots \\ b_{K} \end{pmatrix} \)
【本編】多クラスロジスティック回帰の流れを整理
STEP1:分布の種類を仮定(シグモイド関数)【Excel】
・「多クラス」のロジスティクス回帰なので活性化関数には「ソフトマックス関数」を使用
・K個のクラスに分類する場合、次の式で表現できます。
\( softmax(x)_{i} = \frac{e^xi}{\sum^{K}_{j=1} e^{xj}} \) \( \quad (i=1,2,…,K) \)
⇒\( \sum^{K}_{j=1} e^{x_j} = 1\)であり、確率として表現できる点がポイントです。
STEP2:尤度関数を設定
・①確率密度関数の一般式
・ある入力電気信号「\( \boldsymbol{x} \)」に対して、ニューロンがクラス「\( k \)」に分類される確率(確率変数\(C= k \)とする)
\( Pr(C=k|\boldsymbol{x}) \)
\( \quad= softmatx( \boldsymbol{w_k}^\mathsf{T} \cdot \boldsymbol{x}+b_k ) \)
\( \quad= \frac{exp(\boldsymbol{w_k}^\mathsf{T} \cdot \boldsymbol{x}+b_k)}{\sum^{K}_{j=1} exp(\boldsymbol{w_j}^\mathsf{T} \cdot \boldsymbol{x}+b_j)} \)
\( \quad= y_k \)
・②確率密度関数の一般式(別の表現)
これは表現を変えると、ある重み「\(\boldsymbol{w_k}^\mathsf{T}\)」とあるバイアス「\(b_k\)」の元で、入力電気信号が「\(x\)」になる確率とも表せます。
\( Pr(\boldsymbol{x}|\boldsymbol{w_k}^\mathsf{T},b_k) \)
\( \quad= softmatx( \boldsymbol{w_k}^\mathsf{T} \cdot \boldsymbol{x}+b_k ) \)
\( \quad= \frac{exp(\boldsymbol{w_k}^\mathsf{T} \cdot \boldsymbol{x}+b_k)}{\sum^{K}_{j=1} exp(\boldsymbol{w_j}^\mathsf{T} \cdot \boldsymbol{x}+b_j)} \)
\( \quad= y_k \)
・③確率密度関数の一般式(入力N個の場合)
また、\(N\)個の入力データ\(\boldsymbol{x_n} (n=1,2,…)\)と、それに対応する正解データ\(\boldsymbol{t_n}\)が与えられた場合、確率は総乗として表現できる。
\( Pr(\boldsymbol{x_n}| \boldsymbol{w_k}^\mathsf{T},b_k) = \displaystyle \prod_{n=1}^N y_{nk}^{t_{nk}} \)
※ \(t_{j}=0 (j≠k) \)、 \(t_{j}=1 (j=k) \) ⇒正解の時のみ1が立つ
※\( y_{nk} \)を\( t_{nk} \)乗している理由は、\( j≠k \)の時は0乗(=1)として、項を無効化するため。
\( W,b \)を推定するための「
尤度関数」を求めるためには、更に\( y \)方向に総乗します。
\( Pr(\boldsymbol{x_n}| \boldsymbol{W},\boldsymbol{b}) = \displaystyle \prod_{n=1}^N \prod_{k=1}^K y_{nk}^{t_{nk}} \)
・④尤度関数
\( L(\boldsymbol{W},\boldsymbol{b} | \boldsymbol{x_n}) = \displaystyle \prod_{n=1}^N \prod_{j=1}^K y_{nk}^{t_{nk}} \)
STEP3:片方パラメータ(重みw)を固定して「バイアスb」を推定
STEP4:もう片方のパラメータ(バイアスb)を固定して「重みw」を推定
・①誤差関数(尤度関数の対数)
\( E(\boldsymbol{W},\boldsymbol{b}|\boldsymbol{x_n}) \)
\( \quad= -\frac{1}{N} \log L(\boldsymbol{W},\boldsymbol{b}|\boldsymbol{x_n}) \)
\( \quad= -\frac{1}{N} \sum^{N}_{n=1} \sum^{K}_{k=1} t_{nk} \log y_{nk} \)
・②勾配降下法
・まずは簡単のため \( w_{j}, b_{j} \)の勾配を求めます。このとき、\( a_n = W \boldsymbol{x_n}+\boldsymbol{b} \)と置きます。
\( \boldsymbol{w_j}^{(k+1)} \)
\( \quad=\boldsymbol{w_j}^{(k)}-\eta \frac{\partial E(\boldsymbol{W},\boldsymbol{b})}{\partial \boldsymbol{w_j}} \)
\( \quad=\boldsymbol{w_j}^{(k)}-\eta \lbrace – \frac{1}{N} \sum^{N}_{n=1} \sum^{K}_{k=1} \frac{\partial }{\partial y_{nk}} (t_{nk} \log y_{nk}) \frac{\partial y_{nk}}{\partial a_{nj}} \frac{\partial a_{nj}}{\partial \boldsymbol w_{j}} \rbrace \)
このとき、\( \frac{\partial a_{nj}}{\partial \boldsymbol{w_{j}}} = \boldsymbol{x_n} \)であるため、
\( \quad=\boldsymbol{w_j}^{(k)}-\eta \lbrace – \frac{1}{N} \sum^{N}_{n=1} \sum^{K}_{k=1} \frac{ t_{nk} }{ y_{nk} } \frac{\partial y_{nk}}{\partial a_{nj}} \boldsymbol{x_n} \rbrace \)
また、
ソフトマックス関数の微分から、\( \frac{\partial y_k}{\partial a_j} = y_{k} ( I_{kj} – y_{j}) \)と変形できるため、次のようになる。
\( \quad=\boldsymbol{w_j}^{(k)}-\eta \lbrace – \frac{1}{N} \sum^{N}_{n=1} \sum^{K}_{k=1} \frac{ t_{nk} }{ y_{nk} } y_{nk} ( \boldsymbol{I_{kj}} – y_{nj}) \boldsymbol{x_n} \rbrace \)
\( \quad=\boldsymbol{w_j}^{(k)}-\eta \lbrace – \frac{1}{N} \sum^{N}_{n=1} \sum^{K}_{k=1} t_{nk} ( \boldsymbol{I_{kj}} – y_{nj}) \boldsymbol{x_n} \rbrace \)
ここで、\( \sum^{K}_{k=1} t_{nk} ( \boldsymbol{I_{kj}} – y_{nj}) \)に着目すると、\( \sum^{K}_{k=1} t_{nk} \boldsymbol{I_{kj}} \)は\( k=j \)の時以外は0になり\( t_{nj} \)と変形できる。
加えて、\( \sum^{K}_{k=1} t_{nk} y_{nj} \)も\( k=j \)の時は\( t_{nk} = 1 \)で、それ以外は\( t_{nk}=0 \)になるため\( y_{nj} \)と変形できる。よって、
\( \quad=\boldsymbol{w_j}^{(k)}-\eta \lbrace – \frac{1}{N} \sum^{N}_{n=1} (t_{nj}-y_{nj}) \boldsymbol{x_n} \rbrace \)
\( \quad=\boldsymbol{w_j}^{(k)}+\eta \frac{1}{N} \sum^{N}_{n=1} (t_{nj}-y_{nj}) \boldsymbol{x_n} \)
\( b_j^{(k+1)} \)
\( \quad=b_j^{(k)}-\eta \frac{\partial E(\boldsymbol{w},b)}{\partial b_j} \)
\( \quad=b_j^{(k)}-\eta \lbrace – \frac{1}{N} \sum^{N}_{n=1} (t_{nj}-y_{nj}) \rbrace \)
\( \quad=b_j^{(k)}+\eta \frac{1}{N} \sum^{N}_{n=1} (t_{nj}-y_{nj}) \)
・よって、 \( \boldsymbol{W} = ( \boldsymbol{w_1}, \boldsymbol{w_2}, \cdots, \boldsymbol{w_K} )^\mathsf{T}, \boldsymbol{b} = (b_1,b_2,\cdots,b_K) \)の勾配は次のように求まります。
\( \boldsymbol{W}^{(k+1)} \)
\( \quad=\boldsymbol{W}^{(k)}+\eta \frac{1}{N} \sum^{N}_{n=1} ( \boldsymbol{t_{n}}-\boldsymbol{y_{n}}) \boldsymbol{x_n} \)
\( \boldsymbol{b}^{(k+1)} \)
\( \quad=\boldsymbol{b}^{(k)}+\eta \frac{1}{N} \sum^{N}_{n=1} ( \boldsymbol{t_{n}}-\boldsymbol{y_{n}}) \)
・③確率的勾配降下法【Excel】
\( \boldsymbol{W}^{(k+1)} \)
\( \quad=\boldsymbol{W}^{(k)}+\eta ( \boldsymbol{t_{n}}-\boldsymbol{y_{n}}) \boldsymbol{x_n} \)
\( \boldsymbol{b}^{(k+1)} \)
\( \quad=\boldsymbol{b}^{(k)} +\eta ( \boldsymbol{t_{n}}-\boldsymbol{y_{n}}) \)
STEP5:尤度関数の最大値(=傾き0=偏微分が0)を求める【Excel】
→繰り返しにより求める
(参考)
尤度関数や最尤推定の考え方や内容を知りたい方は、下記記事も併せてご覧ください。
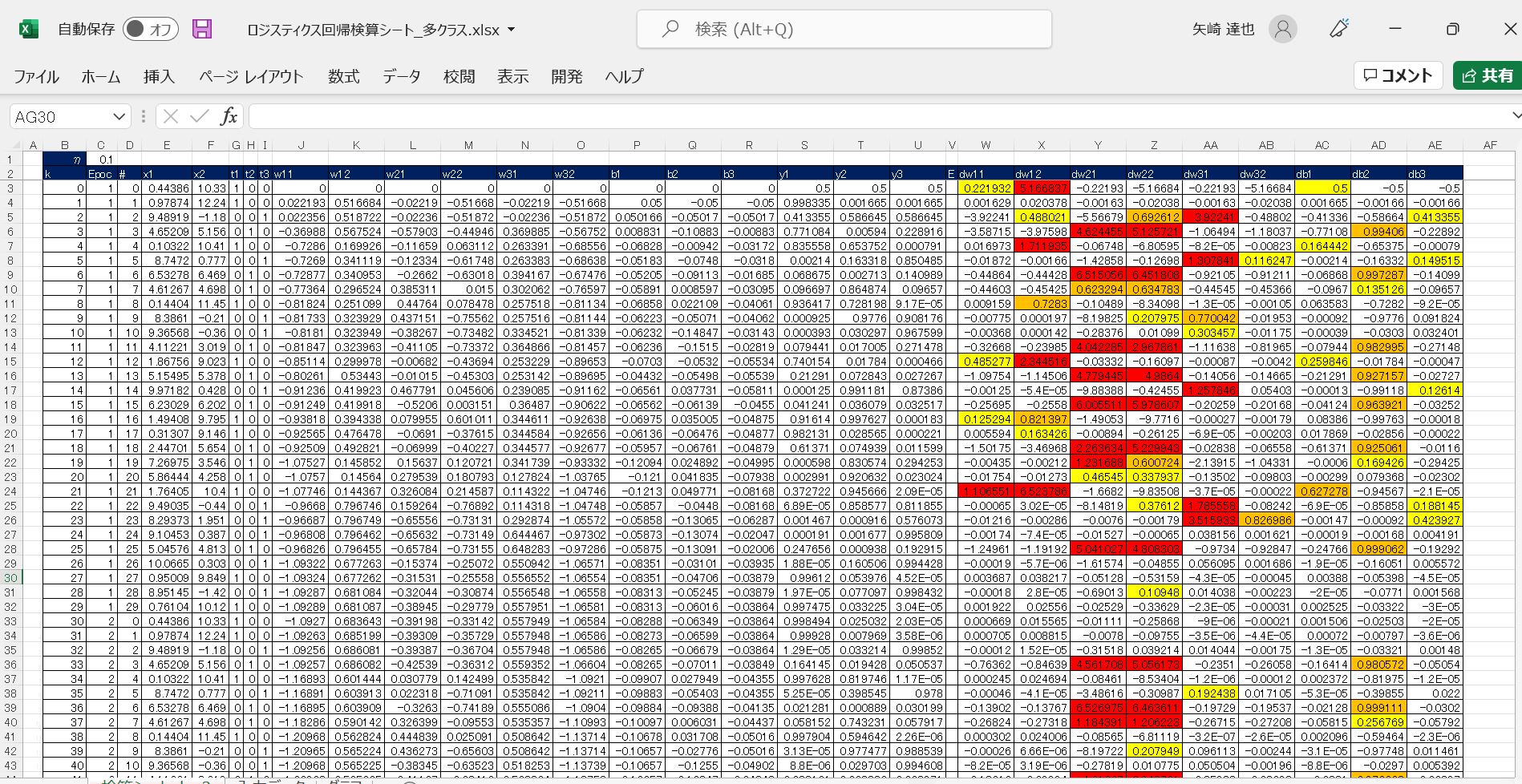
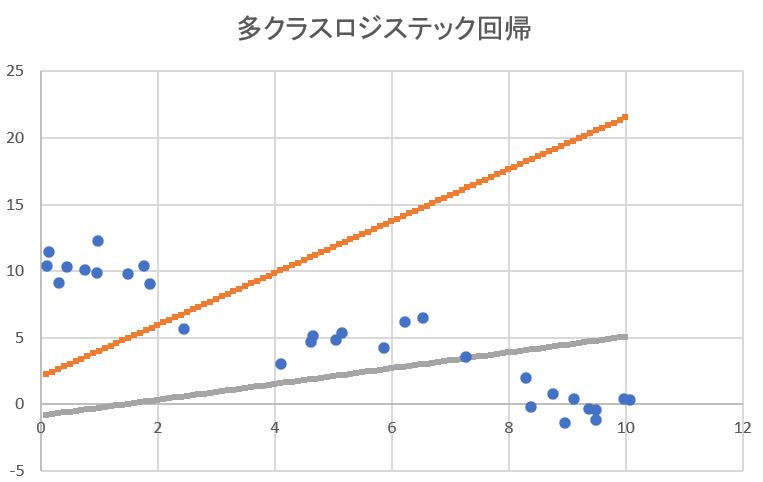
【オマケ】多クラスのロジスティック回帰をExcelで計算