<目次>
多層パーセプトロンのアルゴリズムをご紹介(Excel計算のオマケ付き)
【前提①】多層パーセプトロンとは?
多層パーセプトロンの流れを整理
●STEP1:分布の種類を仮定(シグモイド関数)【Excel】
●STEP2:尤度関数を設定
●STEP3:片方パラメータ(重みw)を固定して「バイアスb」を推定
●STEP4:もう片方のパラメータ(バイアスb)を固定して「重みw」を推定
●STEP5:尤度関数の最大値(=傾き0=偏微分が0)を求める【Excel】
【オマケ】多層パーセプトロンをExcelで計算
多層パーセプトロンのアルゴリズムをご紹介(Excel計算のオマケ付き)
【前提①】多層パーセプトロンとは?
- ニューラルネットワークのモデルの種類の1つで、入力層と出力層の間に「隠れ層」があり「非線形分類」ができるのが特徴です。
- 基本的な論理ゲート(AND、OR、NOT)は1本の線で分類(発火する/しない)を表現可。
- しかしXORは特殊な回路で、1本の線では表現できません(線形分離不可)
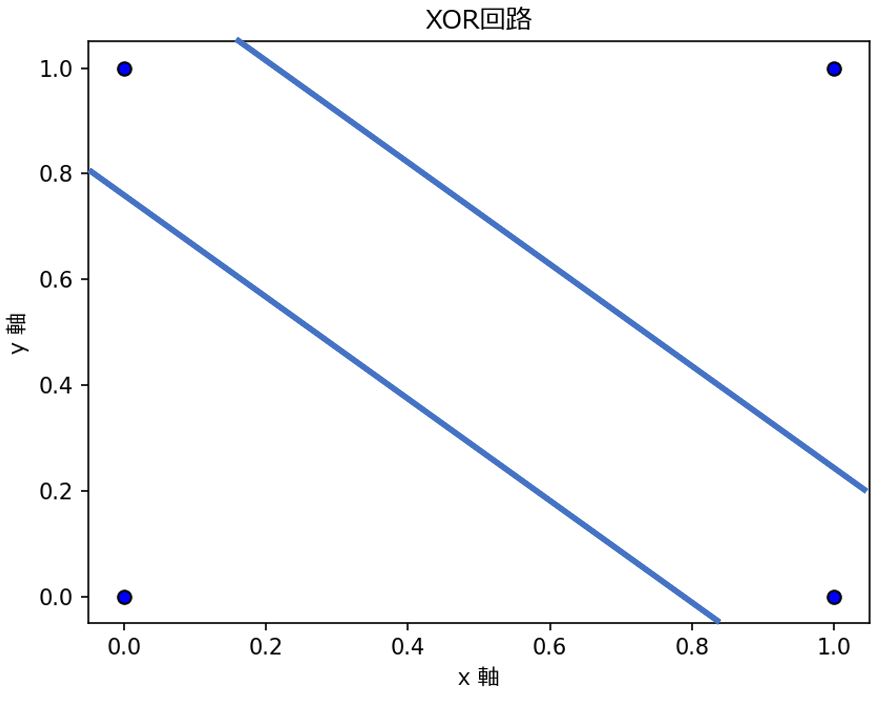
- 基本的なモデルである「単純パーセプトロン」や「ロジスティック回帰」はあくまで「線形分類」です。
- しかし、基本の論理ゲートを組み合わせる事でXOR回路を実現可能です。
- 論理ゲート(破線部)をニューロンに見立てる(h1、h2)ことで「非線形分類」のモデルが作れます。
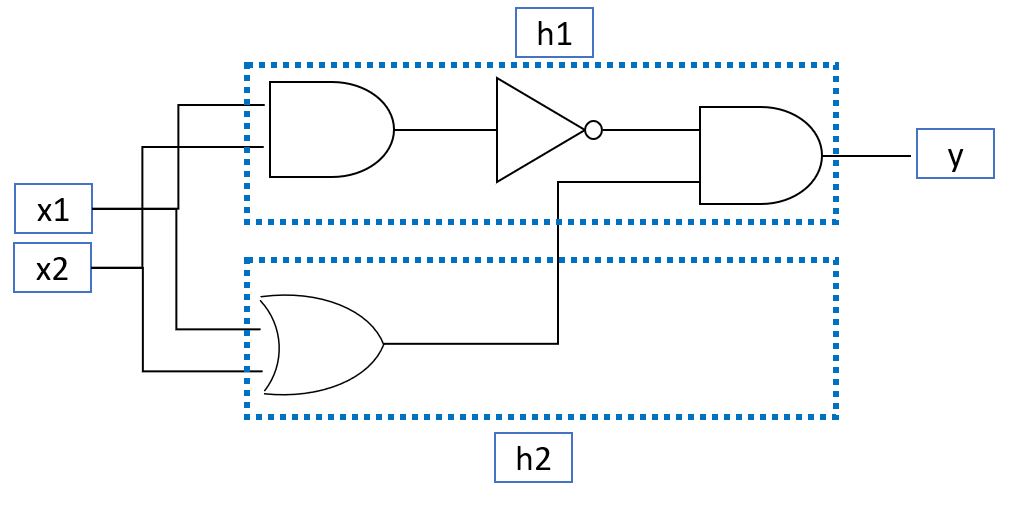
- このような入力と出力以外の層があるニューラルネットワークモデルを「多層パーセプトロン」と呼びます。
- 入力層と出力層の間にある層を「隠れ層」と呼びます。

↓

この時活性化関数\( f( \cdot ) \)、\( g( \cdot ) \)は活性化関数で、\( y, V, c, h, W, b \)はそれぞれ以下の通り。
\( \boldsymbol{x} = \begin{pmatrix} x_1 \\ \vdots \\ x_j \\ \vdots \\ x_{M} \end{pmatrix} \)
\( \boldsymbol{h} = \begin{pmatrix} h_1 \\ \vdots \\ h_j \\ \vdots \\ h_{J} \end{pmatrix} \boldsymbol{W} = \begin{pmatrix} w_{11} & \cdots & w_{1m} & \cdots & w_{1M} \\ \vdots \\ w_{j1} & \cdots & w_{jm} & \cdots & w_{jM} \\ \vdots \\ w_{J1} & \cdots & w_{Jm} & \cdots & w_{JM} \end{pmatrix} \boldsymbol{b} = \begin{pmatrix} b_1 \\ \vdots \\ b_j \\ \vdots \\ b_{J} \end{pmatrix} \)
\( \boldsymbol{y} = \begin{pmatrix} y_1 \\ \vdots \\ y_k \\ \vdots \\ y_{K} \end{pmatrix} \boldsymbol{V} = \begin{pmatrix} v_{11} & \cdots & v_{1j} & \cdots & v_{1J} \\ \vdots \\ v_{k1} & \cdots & v_{kj} & \cdots & v_{kJ} \\ \vdots \\ v_{K1} & \cdots & v_{Kj} & \cdots & v_{KJ} \end{pmatrix} \boldsymbol{c} = \begin{pmatrix} c_1 \\ \vdots \\ c_k \\ \vdots \\ c_{K} \end{pmatrix} \)
(図111)
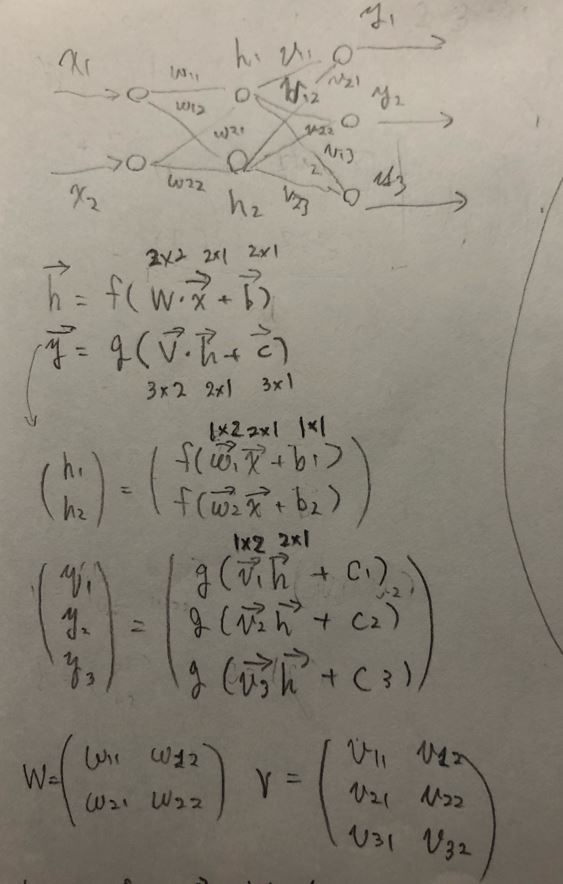
多層パーセプトロンの流れを整理
●STEP1:分布の種類を仮定(シグモイド関数)【Excel】
多層パーセプトロンの「出力層\( y \)」と「隠れ層\( h \)」活性化関数は「2値分類⇒シグモイド、多クラス分類⇒ソフトマックス」を使い分ける。
・2個のクラスに分類する場合 ⇒\( \quad \sigma(x) = \frac{1}{1+e^{-x}} \)
・K個のクラスに分類する場合 ⇒\( \quad softmax(x_{i}) = \frac{e^xi}{\sum^{K}_{j=1} e^{xj}} \) \( \quad (i=1,2,…,K) \)
⇒\( \sum^{K}_{j=1} e^{x_j} = 1\)であり、確率として表現できる点がポイントです。
●STEP2:尤度関数を設定
⇒省略
- (a)「2値分類」の場合は「こちらの記事のSTEP2」を参照。
\( \quad\quad L(\boldsymbol{w},\boldsymbol{v},b,c| \boldsymbol{x_n})= \displaystyle \prod_{n=1}^N {y_n}^{t_n} (1-y_n)^{1-t_n} \)
- (b)「多クラス分類」の場合は「こちらの記事のSTEP2」を参照。
\( \quad\quad L(\boldsymbol{W},\boldsymbol{V},\boldsymbol{b},\boldsymbol{c} | \boldsymbol{x_n}) = \displaystyle \prod_{n=1}^N \prod_{k=1}^K y_{nk}^{t_{nk}} \)
●STEP3:片方パラメータ(重みw)を固定して「バイアスb」を推定
●STEP4:もう片方のパラメータ(バイアスb)を固定して「重みw」を推定
・①誤差関数(尤度関数の対数)
- ⇒(a)「2値分類」の場合
\( \quad= -\frac{1}{N} \sum^{N}_{n=1} \lbrace {t_n}\log{y_n} + (1-t_n) \log (1-y_n) \rbrace \)
- ⇒(b)「多クラス分類」の場合
\( \quad= -\frac{1}{N} \sum^{N}_{n=1} \sum^{K}_{k=1} t_{nk} \log y_{nk} \)
・②勾配降下法
まずは簡単のため \( \boldsymbol{v_{k}}, c_{k}, \boldsymbol{w_{j}}, b_{j} \)の勾配を求めます。このとき、\( \boldsymbol{p} = W \boldsymbol{x}+\boldsymbol{b} \)、\( \boldsymbol{q} = V \boldsymbol{h}+\boldsymbol{c} \)と置きます。
==================
このとき、\( \frac{\partial q_{k}}{\partial \boldsymbol{v_{k}}} = \boldsymbol{h} \)であるため、
\( \quad=\boldsymbol{v_k}^{(i)}-\eta \frac{\partial E}{\partial q_{k}} \boldsymbol{h} \)
==================
\( \quad=c_k^{(i)}-\eta \frac{\partial E(W,V,\boldsymbol{b},\boldsymbol{c})}{\partial c_{k}} \)
\( \quad=c_k^{(i)}-\eta \frac{\partial E}{\partial q_{k}} \frac{ \partial q_{k}}{\partial c_{k} } \)
このとき、\( \frac{\partial q_{k}}{\partial c_{k}} = 1 \)であるため、
==================
\( \quad=\boldsymbol{w_j}^{(i)}-\eta \frac{\partial E(W,V,\boldsymbol{b},\boldsymbol{c})}{\partial \boldsymbol{w_j}} \)
このとき、\( \frac{\partial p_{j}}{\partial \boldsymbol{w_{j}}} = \boldsymbol{x} \)であるため、
また、偏微分の連鎖律より\( \frac{\partial E}{\partial p_{j}} = \frac{\partial E}{\partial q_{1}} \frac{\partial q_{1}}{\partial p_{j}} + \frac{\partial E}{\partial q_{2}} \frac{\partial q_{2}}{\partial p_{j}} + \cdots + \frac{\partial E}{\partial q_{k}} \frac{\partial q_{k}}{\partial p_{j}} = \sum^{K}_{k=1} \frac{\partial E}{\partial q_{k}} \frac{\partial q_{k}}{\partial p_{j}} \)であり、
更に、合成関数の微分より、\( \frac{\partial q_{k}}{\partial p_{j}} = \frac{\partial ( \boldsymbol{v_{k}} \boldsymbol{h} + c_{k} )}{\partial p_{j}} = \frac{\partial ( \boldsymbol{v_{k}} f(\boldsymbol{p}) + c_{k} )}{\partial p_{j}} \)となり、隠れ層の\(j\)番目の成分のみが残るため\( \frac{\partial ( \boldsymbol{v_{k}} f(\boldsymbol{p}) + c_{k} )}{\partial p_{j}} = v_{kj} f^{\prime}(p_{j}) \)となる。
\( f^{\prime}(p_{j}) \)はシグモイド関数やソフトマックス関数の微分により\( f(p_{j})(1-f(p_{j})) \)なので、
\( b_j^{(i+1)} \)
\( \quad=b_j^{(i)}-\eta \frac{\partial E(W,V,\boldsymbol{b},\boldsymbol{c})}{\partial b_j} \)
このとき、\( \frac{\partial p_{j}}{\partial b_{j}} = 1 \)であるため、
\( \quad=b_j^{(i)}-\eta f(p_{j})(1-f(p_{j})) \sum^{K}_{k=1} \frac{\partial E}{\partial q_{k}} v_{kj} \)
(図112)

よって、 \( \boldsymbol{V} = ( \boldsymbol{v_1}, \boldsymbol{v_2}, \cdots, \boldsymbol{v_K} )^\mathsf{T}, \boldsymbol{c} = (c_1,c_2,\cdots,c_K), \boldsymbol{W} = ( \boldsymbol{w_1}, \boldsymbol{w_2}, \cdots, \boldsymbol{w_J} )^\mathsf{T}, \boldsymbol{b} = (b_1,b_2,\cdots,b_J) \)の勾配は次のように求まります。
\( \boldsymbol{W}^{(i+1)} \)
\( \boldsymbol{b}^{(i+1)} \)
・③確率的勾配降下法
(図113)

●STEP5:尤度関数の最大値(=傾き0=偏微分が0)を求める【Excel】
【オマケ】多層パーセプトロンをExcelで計算