多クラスのロジスティック回帰をKerasで実装した例をご紹介

import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD
from sklearn.utils import shuffle

# 入力xの次元
M = 2
# 出力yの次元（クラス数）
K = 3
# 入力データセットの総
nc = 10
# 入力データセットの総数
N = nc * K
# ミニバッチのサイズ
mini_batch_size = 5

def mc_logistic_regression(Xarg,targ):
    ############################################
    # STEP1：モデルの定義
    ############################################

    # 入力の電気信号xの初期化
    X = np.array(Xarg)
    # 正解値tの定義
    t = np.array(targ)
    
    # 入力層 - 出力層の定義
    # 　Dense(input_dim=M, units=K)：入力がM次元、出力がK次元のネットワーク
    # 　　⇒ W[K行×M列] × xn[M行×1列] + b[K行×1列]に相当
    # 　Activation('softmax')：活性化関数として、シグモイド関数を指定
    # 　　⇒ y = e^{xi}/Σe^{xi} = softmax(Wx + b)に相当
    model = Sequential([
        Dense(input_dim=M, units=K),
        Activation('softmax')
    ])

    # 別の記述方法：add関数でも記述可能
    #model = Sequential()
    #model.add(Dense(input_dim=M, units=K))
    #model.add(Activation('softmax'))

    ############################################
    # STEP2：誤差関数の定義
    ############################################
    # ⇒今回は不要
    # （確率的勾配降下法を使うため、誤差関数Eは計算不要）

    ############################################
    # STEP3：最適化手法の定義（例：確率的勾配降下法）
    ############################################

    # loss='categorical_crossentropy'
    # 　誤差関数の種類を指定。
    # 　多クラス値（例：晴、雨、曇、雷、雪）の交差エントロピー関数の計算をさせる。
    # SGD(lr=0.1)
    # 　最適化の手法を指定している。「SGD」は確率的勾配降下法で「lr」はその学習率。
    # 　それぞれ「Stochastic Gradient Descent」と「learning rate」の頭文字を取っている。
    model.compile(loss='categorical_crossentropy',optimizer=SGD(lr=0.1))

    ############################################
    # STEP4：セッションの初期化
    ############################################
    # ⇒今回は不要
    # （TensorFlow v2以降はSessionを使用しないため）

    ############################################
    # STEP5：学習
    ############################################
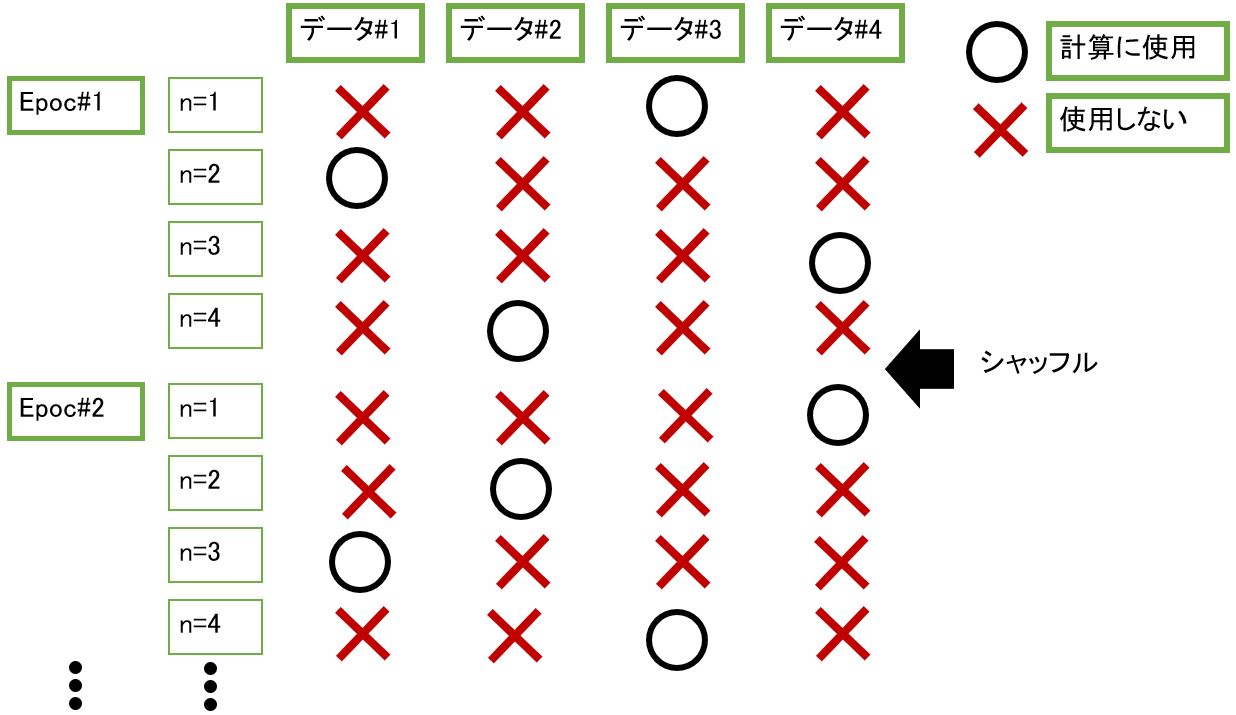
    # データをシャッフル
    X_,t_ = shuffle(X,t)

    # 指定したエポック数、繰り返し学習を行う
    # 　第1引数：Xは入力データ（入力の電気信号）
    # 　第2引数：tは正解データ（出力の電気信号の正解値）
    # 　第3引数：エポック（データ全体に対する反復回数）の数
    # 　第4引数：ミニバッチ勾配降下法（N個の入力データをM個ずつのグループに分けて学習する際のMの値）
    model.fit(X_,t_,epochs=10,batch_size=mini_batch_size)

    ############################################
    # STEP6：学習結果の確認
    ############################################

    # 分類が正しい結果になっているか？の確認
    # model.predict(X_,batch_size=mini_batch_size)
    # 　⇒各「入力」に対する「出力」の確率（ソフトマックス）の確認
    # np.argmax(●)で[X,X,X]の最大のインデックスを抽出
    # (例) [[0,1,0],[0,0,1],[1,0,0]]⇒[1,2,0]
    # axis=1の場合は横軸単位で比較する。
    # axis=0の場合は縦軸同士で比較する。
    classes = np.argmax(model.predict(X_,batch_size=mini_batch_size),axis=1)
    # 正解のインデックス情報
    # 　t_でデータ数N回ループし、正解のindexを抽出してリスト化け
    #　 (例)[[0,1,0],[0,0,1],[1,0,0]]⇒[1,2,0]
    t_index = np.argmax(t_,axis=1)    
    # 別の方法で、forループを使ったワンライナーでも記述可能。
    #t_index = [index for i in range(len(t_)) for index in range(K) if t_[i][index] == 1]
    # ネットワークの出力「y」の計算結果を取得
    prob = model.predict(X_,batch_size=mini_batch_size)

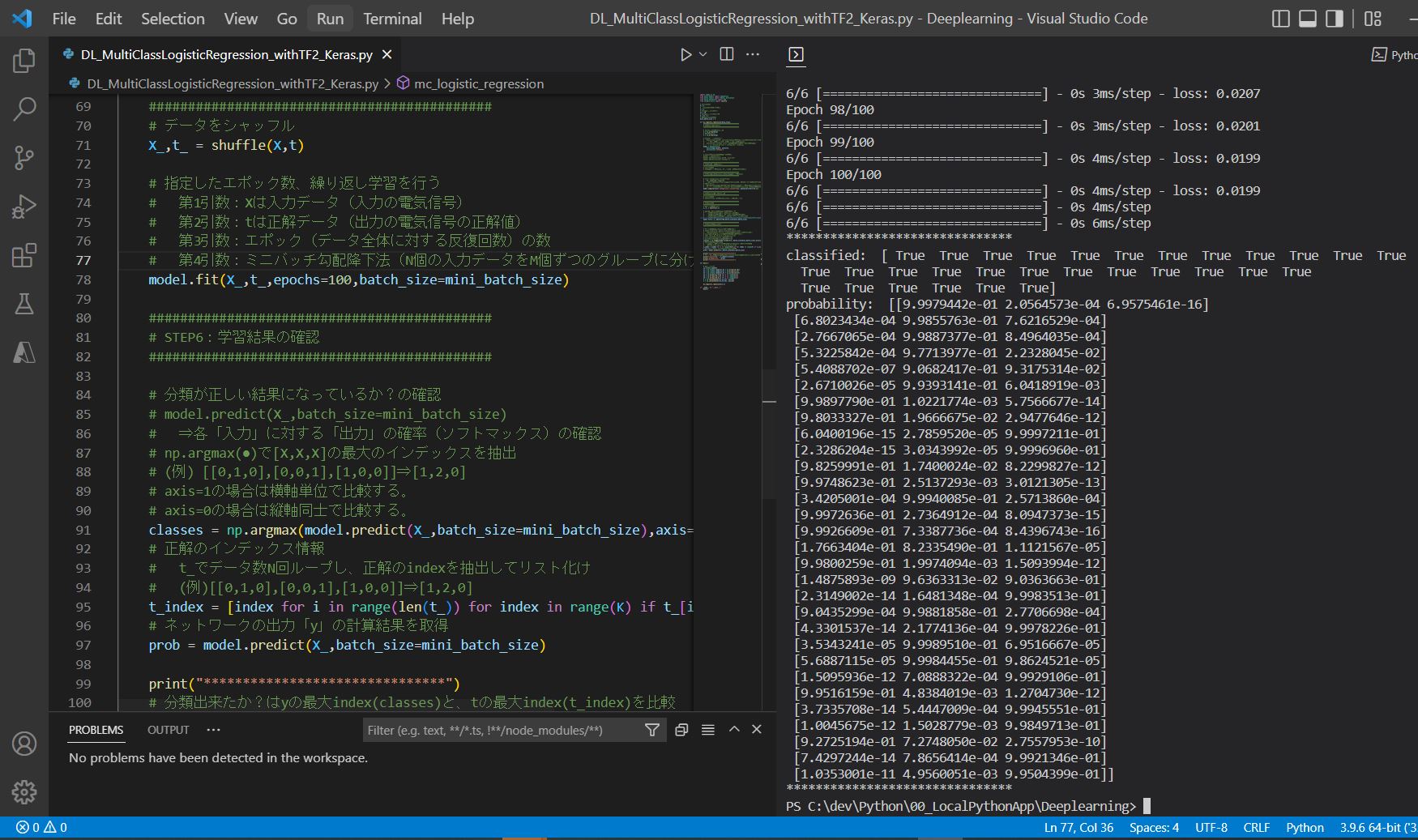
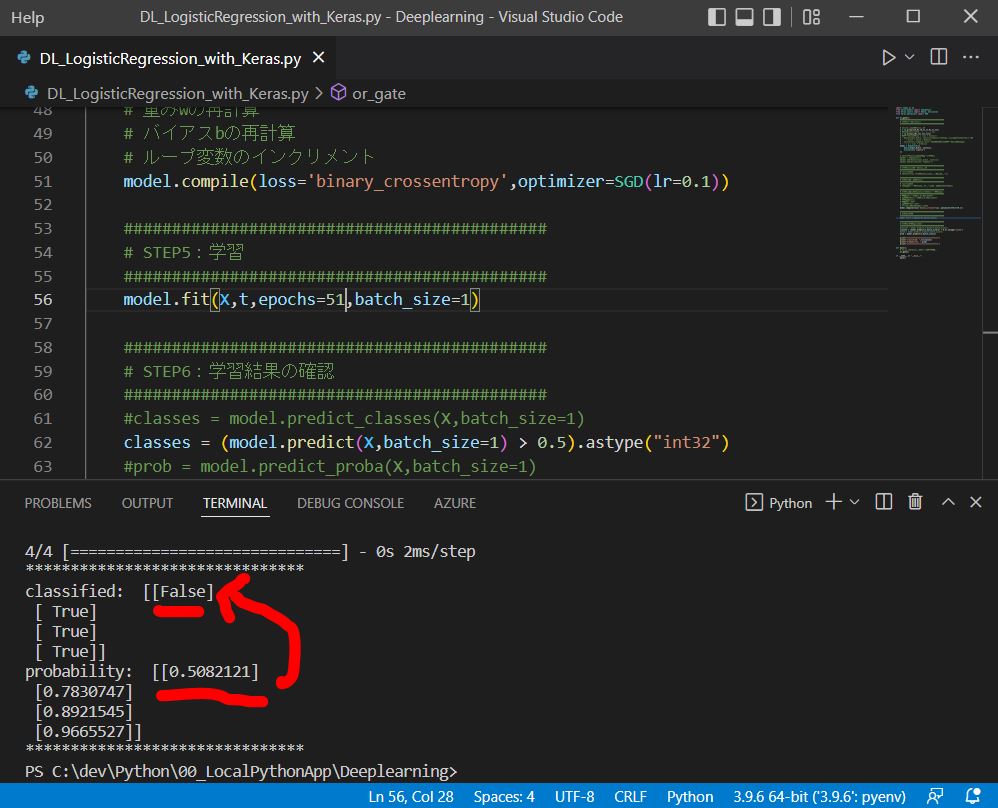
    print("*******************************")
    # 分類出来たか？はyの最大index(classes)と、tの最大index(t_index)を比較
    print("classified: ",t_index==classes)
    print("probability: ",prob)
    print("*******************************")

def main():

    # データセット
    np.random.seed(0)
    X1 = np.random.randn(nc,M) + np.array([0,10])
    X2 = np.random.randn(nc,M) + np.array([5,5])
    X3 = np.random.randn(nc,M) + np.array([10,0])
    t1 = np.array([[1,0,0] for i in range(nc)])
    t2 = np.array([[0,1,0] for i in range(nc)])
    t3 = np.array([[0,0,1] for i in range(nc)])
    X = np.concatenate((X1,X2,X3), axis=0)
    t = np.concatenate((t1,t2,t3), axis=0)

    mc_logistic_regression(X,t)
  
if __name__ == "__main__":
    main()

（実行結果）

Epoch 1/100
6/6 [==============================] - 1s 2ms/step - loss: 1.1570
Epoch 2/100
6/6 [==============================] - 0s 3ms/step - loss: 0.2156
～中略～
Epoch 99/100
6/6 [==============================] - 0s 4ms/step - loss: 0.0199
Epoch 100/100
6/6 [==============================] - 0s 4ms/step - loss: 0.0199
*******************************
classified:  [ True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True]
probability:  [[9.9979442e-01 2.0564573e-04 6.9575461e-16]
 [6.8023434e-04 9.9855763e-01 7.6216529e-04]
 [2.7667065e-04 9.9887377e-01 8.4964035e-04]
 [5.3225842e-04 9.7713977e-01 2.2328045e-02]
 [5.4088702e-07 9.0682417e-01 9.3175314e-02]
 [2.6710026e-05 9.9393141e-01 6.0418919e-03]
 [9.9897790e-01 1.0221774e-03 5.7566677e-14]
 [9.8033327e-01 1.9666675e-02 2.9477646e-12]
 [6.0400196e-15 2.7859520e-05 9.9997211e-01]
 [2.3286204e-15 3.0343992e-05 9.9996960e-01]
 [9.8259991e-01 1.7400024e-02 8.2299827e-12]
 [9.9748623e-01 2.5137293e-03 3.0121305e-13]
 [3.4205001e-04 9.9940085e-01 2.5713860e-04]
 [9.9972636e-01 2.7364912e-04 8.0947373e-15]
 [9.9926609e-01 7.3387736e-04 8.4396743e-16]
 [1.7663404e-01 8.2335490e-01 1.1121567e-05]
 [9.9800259e-01 1.9974094e-03 1.5093994e-12]
 [1.4875893e-09 9.6363313e-02 9.0363663e-01]
 [2.3149002e-14 1.6481348e-04 9.9983513e-01]
 [9.0435299e-04 9.9881858e-01 2.7706698e-04]
 [4.3301537e-14 2.1774136e-04 9.9978226e-01]
 [3.5343241e-05 9.9989510e-01 6.9516667e-05]
 [5.6887115e-05 9.9984455e-01 9.8624521e-05]
 [1.5095936e-12 7.0888322e-04 9.9929106e-01]
 [9.9516159e-01 4.8384019e-03 1.2704730e-12]
 [3.7335708e-14 5.4447009e-04 9.9945551e-01]
 [1.0045675e-12 1.5028779e-03 9.9849713e-01]
 [9.2725194e-01 7.2748050e-02 2.7557953e-10]
 [7.4297244e-14 7.8656414e-04 9.9921346e-01]
 [1.0353001e-11 4.9560051e-03 9.9504399e-01]]
*******************************

（図１２１）