<目次>
多層パーセプトロンで隠れ層が複数ある場合のアルゴリズム
前提:多層パーセプトロンとは?
多層パーセプトロンモデルの出力式
多層パーセプトロンの流れ(隠れ層が複数ある場合)
●STEP1:分布の種類を仮定(シグモイド関数)【Excel】
●STEP2:尤度関数を設定
●STEP3:片方パラメータ(重みw)を固定して「バイアスb」を推定
●STEP4:もう片方のパラメータ(バイアスb)を固定して「重みw」を推定
●STEP5:尤度関数の最大値(=傾き0=偏微分が0)を求める【Excel】
【オマケ】Excel計算
多層パーセプトロンで隠れ層が複数ある場合のアルゴリズム
前提:多層パーセプトロンとは?
→(参考)多層パーセプトロンのアルゴリズム
>目次にもどる
多層パーセプトロンモデルの出力式
ニューロンは、入力を「M個」、隠れ層1を「J個」、隠れ層2を「K個」、出力を「L個」とします。
・隠れ層2→出力層の式(\(l\)番目のニューロン)は
\(y_{l} = f(\boldsymbol{u_{l}}^\mathsf{T} \cdot \boldsymbol{h_{(2)}}+d_{l})\)
・隠れ層2→出力層の式(全体)は
\( \boldsymbol{y} = f(\boldsymbol{U} \boldsymbol{h_{(2)}} + \boldsymbol{d}) \)
・隠れ層1→隠れ層2の式(\(k\)番目のニューロン)は
\(h_{(2)k} = f(\boldsymbol{v_{k}}^\mathsf{T} \cdot \boldsymbol{h_{(1)}}+c_{k})\)
・隠れ層1→隠れ層2の式(全体)は
\( \boldsymbol{h_{(2)}} = f(\boldsymbol{V} \boldsymbol{h_{(1)}} + \boldsymbol{c}) \)
・入力層→隠れ層の式(\(j\)番目のニューロン)は
\(h_{(1)j} = f(\boldsymbol{w_{j}}^\mathsf{T} \cdot \boldsymbol{x}+b_{j})\)
・入力層→隠れ層2の式(全体)は
\( \boldsymbol{h_{(1)}} = f(\boldsymbol{W} \boldsymbol{x} + \boldsymbol{b}) \)
(図121)
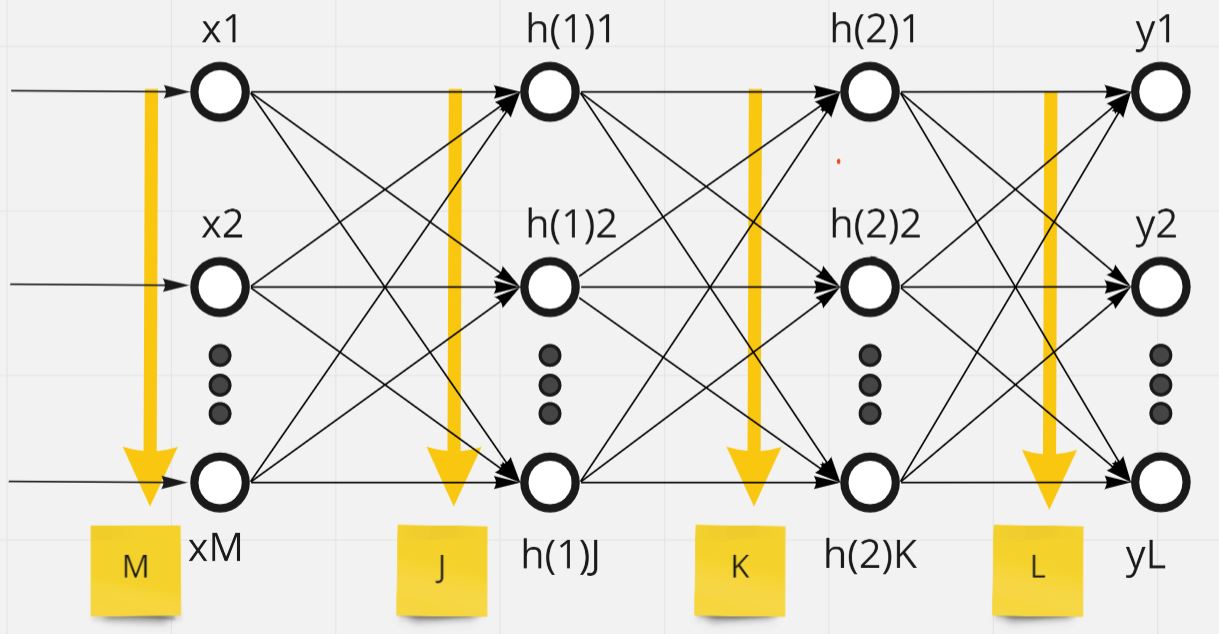
この時活性化関数\( f( \cdot ) \)、\( g( \cdot ) \)は活性化関数で、\( x, y, U, d, h_{2}, V, c, h_{1}, W, b \)はそれぞれ以下の通り。
\( \boldsymbol{x} = \begin{pmatrix} x_1 \\ \vdots \\ x_j \\ \vdots \\ x_{M} \end{pmatrix} \)
\( \boldsymbol{y} = \begin{pmatrix} y_1 \\ \vdots \\ y_l \\ \vdots \\ y_{L} \end{pmatrix}
\boldsymbol{U} = \begin{pmatrix} u_{11} & \cdots & u_{1k} & \cdots & v_{1K} \\ \vdots \\ v_{l1} & \cdots & v_{lk} & \cdots & v_{lK} \\ \vdots \\ v_{L1} & \cdots & v_{Lk} & \cdots & v_{LK} \end{pmatrix}
\boldsymbol{d} = \begin{pmatrix} d_1 \\ \vdots \\ d_l \\ \vdots \\ d_{L} \end{pmatrix} \)
\( \boldsymbol{h_{(2)}} = \begin{pmatrix} h_{(2)1} \\ \vdots \\ h_{(2)k} \\ \vdots \\ h_{(2)K} \end{pmatrix}
\boldsymbol{V} = \begin{pmatrix} v_{11} & \cdots & v_{1j} & \cdots & v_{1J} \\ \vdots \\ v_{k1} & \cdots & v_{kj} & \cdots & v_{kJ} \\ \vdots \\ v_{K1} & \cdots & v_{Kj} & \cdots & v_{KJ} \end{pmatrix}
\boldsymbol{c} = \begin{pmatrix} c_1 \\ \vdots \\ c_k \\ \vdots \\ c_{K} \end{pmatrix} \)
\( \boldsymbol{h_{(1)}} = \begin{pmatrix} h_{(1)1} \\ \vdots \\ h_{(1)j} \\ \vdots \\ h_{(1)J} \end{pmatrix}
\boldsymbol{W} = \begin{pmatrix} w_{11} & \cdots & w_{1m} & \cdots & w_{1M} \\ \vdots \\ w_{j1} & \cdots & w_{jm} & \cdots & w_{jM} \\ \vdots \\ w_{J1} & \cdots & w_{Jm} & \cdots & w_{JM} \end{pmatrix}
\boldsymbol{b} = \begin{pmatrix} b_1 \\ \vdots \\ b_j \\ \vdots \\ b_{J} \end{pmatrix} \)
(図122)

>目次にもどる
多層パーセプトロンの流れ(隠れ層が複数ある場合)
●STEP1:分布の種類を仮定(シグモイド関数)【Excel】
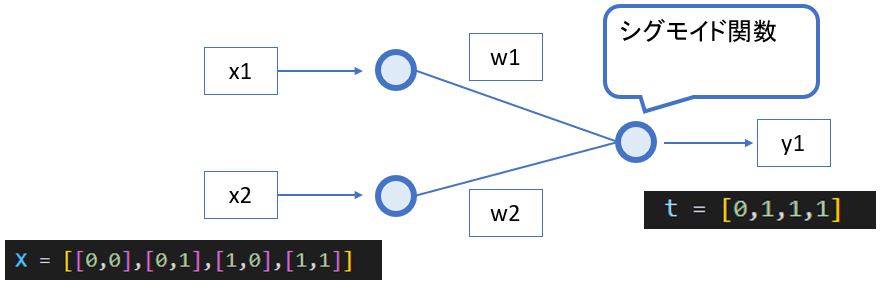
多層パーセプトロンの「出力層\( y \)」と「隠れ層\( h \)」活性化関数は「2値分類⇒シグモイド、多クラス分類⇒ソフトマックス」を使い分ける。
・2個のクラスに分類する場合 ⇒ \( \quad \sigma(x) = \frac{1}{1+e^{-x}} \)
・K個のクラスに分類する場合 ⇒ \( \quad softmax(x_{i}) = \frac{e^xi}{\sum^{K}_{j=1} e^{xj}} \) \( \quad (i=1,2,…,K) \)
⇒\( \sum^{K}_{j=1} e^{x_j} = 1\)であり、確率として表現できる点がポイントです。
●STEP2:尤度関数を設定
⇒省略
⇒(a)「2値分類」の場合は「こちらの記事のSTEP2」を参照。
\( \quad\quad L(\boldsymbol{w},\boldsymbol{v},\boldsymbol{u},b,c,d| \boldsymbol{x_n})= \displaystyle \prod_{n=1}^N {y_n}^{t_n} (1-y_n)^{1-t_n} \)
⇒(b)「多クラス分類」の場合は「こちらの記事のSTEP2」を参照。
\( \quad\quad L(\boldsymbol{W},\boldsymbol{V},\boldsymbol{U},\boldsymbol{b},\boldsymbol{c},\boldsymbol{d} | \boldsymbol{x_n}) = \displaystyle \prod_{n=1}^N \prod_{l=1}^L y_{nl}^{t_{nl}} \)
●STEP3:片方パラメータ(重みw)を固定して「バイアスb」を推定
●STEP4:もう片方のパラメータ(バイアスb)を固定して「重みw」を推定
・①誤差関数(尤度関数の対数)
\( E(\boldsymbol{W},\boldsymbol{V},\boldsymbol{U},\boldsymbol{b},\boldsymbol{c},\boldsymbol{c}|\boldsymbol{x_n}) \)
\( \quad= -\frac{1}{N} \log L(\boldsymbol{W},\boldsymbol{V},\boldsymbol{U},\boldsymbol{b},\boldsymbol{c},\boldsymbol{d}|\boldsymbol{x_n}) \)
⇒(a)「2値分類」の場合
\( \quad= -\frac{1}{N} \sum^{N}_{n=1} \lbrace {t_n}\log{y_n} + (1-t_n) \log (1-y_n) \rbrace \)
⇒(b)「多クラス分類」の場合
\( \quad= -\frac{1}{N} \sum^{N}_{n=1} \sum^{L}_{l=1} t_{nl} \log y_{nl} \)
・②勾配降下法
・まずは簡単のため \( \boldsymbol{u_{l}}, d_{l}, \boldsymbol{v_{k}}, v_{k}, \boldsymbol{w_{j}}, b_{j} \)の勾配を求めます。このとき、\( \boldsymbol{p} = W \boldsymbol{x}+\boldsymbol{b} \)、\( \boldsymbol{q} = V \boldsymbol{h_{(1)}}+\boldsymbol{c} \)、\( \boldsymbol{r} = U \boldsymbol{h_{(2)}}+\boldsymbol{d} \) と置きます。
==================
\( \boldsymbol{u_l}^{(i+1)} \)
\( \quad=\boldsymbol{u_l}^{(i)}-\eta \frac{\partial E(W,V,U,\boldsymbol{b},\boldsymbol{c},\boldsymbol{d})}{\partial \boldsymbol{u_l}} \)
\( \quad=\boldsymbol{u_l}^{(i)}-\eta \frac{\partial E}{\partial r_{l}} \frac{ \partial r_{l}}{\partial \boldsymbol{u_{l}} } \)
このとき、\( \frac{\partial r_{l}}{\partial \boldsymbol{u_{l}}} = \boldsymbol{h_{(2)}} \)であるため、
\( \quad=\boldsymbol{u_l}^{(i)}-\eta \frac{\partial E}{\partial r_{l}} \boldsymbol{h_{(2)}} \)
また、\( \frac{\partial E}{\partial r_{l}}= – \frac{1}{N} \sum^{N}_{n=1} (t_{nl}-y_{nl}) \)であるため、
\( \quad=\boldsymbol{u_l}^{(i)}-\eta \lbrace – \frac{1}{N} \sum^{N}_{n=1} (t_{nl}-y_{nl}) \rbrace \boldsymbol{h_{(2)}} \)
\( \quad=\boldsymbol{u_l}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} (t_{nl}-y_{nl}) \boldsymbol{h_{(2)}} \)
==================
\( d_l^{(i+1)} \)
\( \quad=d_l^{(i)}-\eta \frac{\partial E(W,V,U,\boldsymbol{b},\boldsymbol{c},\boldsymbol{d})}{\partial d_{l}} \)
\( \quad=d_l^{(i)}-\eta \frac{\partial E}{\partial r_{l}} \frac{ \partial r_{l}}{\partial d_{l} } \)
このとき、\( \frac{\partial r_{l}}{\partial d_{k}} = 1 \)であるため、
\( \quad=d_l^{(i)}-\eta \frac{\partial E_{n}}{\partial r_{l}} \)
また、\( \frac{\partial E}{\partial r_{l}}= – \frac{1}{N} \sum^{N}_{n=1} (t_{nl}-y_{nl}) \)であるため、
\( \quad=d_l^{(i)}-\eta \lbrace – \frac{1}{N} \sum^{N}_{n=1} (t_{nl}-y_{nl}) \rbrace \)
\( \quad=d_l^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} (t_{nl}-y_{nl}) \)
==================
\( \boldsymbol{v_k}^{(i+1)} \)
\( \quad=\boldsymbol{v_k}^{(i)}-\eta \frac{\partial E(W,V,U,\boldsymbol{b},\boldsymbol{c},\boldsymbol{d})}{\partial \boldsymbol{v_k}} \)
\( \quad=\boldsymbol{v_k}^{(i)}-\eta \frac{\partial E}{\partial q_{k}} \frac{\partial q_{k}}{\partial \boldsymbol{v_k}} \)
このとき、\( \frac{\partial q_{k}}{\partial \boldsymbol{v_{k}}} = \boldsymbol{x} \)であるため、
\( \quad=\boldsymbol{v_k}^{(i)}-\eta \frac{\partial E}{\partial q_{k}} \boldsymbol{x} \)
また、偏微分の連鎖律より\( \frac{\partial E}{\partial q_{k}} = \frac{\partial E}{\partial r_{1}} \frac{\partial r_{1}}{\partial q_{k}} + \frac{\partial E}{\partial r_{1}} \frac{\partial r_{1}}{\partial q_{k}} + \cdots + \frac{\partial E}{\partial r_{l}} \frac{\partial r_{l}}{\partial q_{k}} = \sum^{L}_{l=1} \frac{\partial E}{\partial r_{l}} \frac{\partial r_{l}}{\partial q_{k}} \)であり、
更に、合成関数の微分より、\( \frac{\partial r_{l}}{\partial q_{k}} = \frac{\partial ( \boldsymbol{u_{l}} \boldsymbol{h_{(2)}} + d_{l} )}{\partial q_{k}} = \frac{\partial ( \boldsymbol{u_{l}} f(\boldsymbol{q}) + d_{l} )}{\partial q_{k}} \)となり、隠れ層の\(k\)番目の成分のみが残るため\( \frac{\partial ( \boldsymbol{u_{l}} f(\boldsymbol{q}) + d_{l} )}{\partial q_{k}} = u_{lk} f^{\prime}(q_{k}) \)となる。
よって\( \frac{\partial E}{\partial q_{k}} = \sum^{L}_{l=1} \frac{\partial E}{\partial r_{l}} \frac{\partial r_{l}}{\partial q_{k}} = \sum^{L}_{l=1} \frac{\partial E}{\partial r_{l}} u_{lk} f^{\prime}(q_{k}) = f^{\prime}(q_{k}) \sum^{L}_{l=1} \frac{\partial E}{\partial r_{l}} u_{lk} \)であるため、元の式に代入すると
\( \quad=\boldsymbol{v_k}^{(i)}-\eta f^{\prime}(q_{k}) \sum^{L}_{l=1} \frac{\partial E}{\partial r_{l}} u_{lk} \boldsymbol{h_{(2)}} \)
\( f^{\prime}(q_{k}) \)はシグモイド関数やソフトマックス関数の微分により\( f(q_{k})(1-f(q_{k})) \)なので、
\( \quad=\boldsymbol{v_k}^{(i)}-\eta f(q_{k})(1-f(q_{k})) \sum^{L}_{l=1} \frac{\partial E}{\partial r_{l}} u_{lk} \boldsymbol{h_{(2)}} \)
==================
\( c_k^{(i+1)} \)
\( \quad=c_k^{(i)}-\eta \frac{\partial E(W,V,U,\boldsymbol{b},\boldsymbol{c},\boldsymbol{d})}{\partial c_k} \)
\( \quad=c_k^{(i)}-\eta \frac{\partial E}{\partial q_{k}} \frac{\partial q_{k}}{\partial c_k} \)
このとき、\( \frac{\partial q_{k}}{\partial c_{k}} = 1 \)であるため、
\( \quad=c_k^{(i)}-\eta \frac{\partial E}{\partial c_{k}} \)
\( \quad=c_k^{(i)}-\eta f(q_{k})(1-f(q_{k})) \sum^{L}_{l=1} \frac{\partial E}{\partial r_{l}} u_{lk} \)
(図131)

==================
\( \boldsymbol{w_j}^{(i+1)} \)
\( \quad=\boldsymbol{w_j}^{(i)}-\eta \frac{\partial E(W,V,U,\boldsymbol{b},\boldsymbol{c},\boldsymbol{d})}{\partial \boldsymbol{w_j}} \)
\( \quad=\boldsymbol{w_j}^{(i)}-\eta \frac{\partial E}{\partial p_{j}} \frac{\partial p_{j}}{\partial \boldsymbol{w_j}} \)
このとき、\( \frac{\partial p_{j}}{\partial \boldsymbol{w_{j}}} = \boldsymbol{x} \)であるため、
\( \quad=\boldsymbol{w_j}^{(i)}-\eta \frac{\partial E}{\partial p_{j}} \boldsymbol{x} \)
また、偏微分の連鎖律より\( \frac{\partial E}{\partial p_{j}} = \frac{\partial E}{\partial q_{1}} \frac{\partial q_{1}}{\partial p_{j}} + \frac{\partial E}{\partial q_{2}} \frac{\partial q_{2}}{\partial p_{j}} + \cdots + \frac{\partial E}{\partial q_{k}} \frac{\partial q_{k}}{\partial p_{j}} = \sum^{K}_{k=1} \frac{\partial E}{\partial q_{k}} \frac{\partial q_{k}}{\partial p_{j}} \)であり、
更に、合成関数の微分より、\( \frac{\partial q_{k}}{\partial p_{j}} = \frac{\partial ( \boldsymbol{v_{k}} \boldsymbol{h_{(1)}} + c_{k} )}{\partial p_{j}} = \frac{\partial ( \boldsymbol{v_{k}} f(\boldsymbol{p}) + c_{k} )}{\partial p_{j}} \)となり、隠れ層の\(j\)番目の成分のみが残るため\( \frac{\partial ( \boldsymbol{v_{k}} f(\boldsymbol{p}) + c_{k} )}{\partial p_{j}} = v_{kj} f^{\prime}(p_{j}) \)となる。
よって\( \frac{\partial E}{\partial p_{j}} = \sum^{K}_{k=1} \frac{\partial E}{\partial q_{k}} \frac{\partial q_{k}}{\partial p_{j}} = \sum^{K}_{k=1} \frac{\partial E}{\partial q_{k}} v_{kj} f^{\prime}(p_{j}) = f^{\prime}(p_{j}) \sum^{K}_{k=1} \frac{\partial E}{\partial q_{k}} v_{kj} \)であるため、元の式に代入すると
\( \quad=\boldsymbol{w_j}^{(i)}-\eta f^{\prime}(p_{j}) \sum^{K}_{k=1} \frac{\partial E}{\partial q_{k}} v_{kj} \boldsymbol{x} \)
\( f^{\prime}(p_{j}) \)はシグモイド関数やソフトマックス関数の微分により\( f(p_{j})(1-f(p_{j})) \)なので、
\( \quad=\boldsymbol{w_j}^{(i)}-\eta f(p_{j})(1-f(p_{j})) \sum^{K}_{k=1} \frac{\partial E}{\partial q_{k}} v_{kj} \boldsymbol{x} \)
==================
\( b_j^{(i+1)} \)
\( \quad=b_j^{(i)}-\eta \frac{\partial E(W,V,U,\boldsymbol{b},\boldsymbol{c},\boldsymbol{d})}{\partial b_j} \)
\( \quad=b_j^{(i)}-\eta \frac{\partial E}{\partial p_{j}} \frac{\partial p_{j}}{\partial b_j} \)
このとき、\( \frac{\partial p_{j}}{\partial b_{j}} = 1 \)であるため、
\( \quad=b_j^{(i)}-\eta \frac{\partial E}{\partial p_{j}} \)
\( \quad=b_j^{(i)}-\eta f(p_{j})(1-f(p_{j})) \sum^{K}_{k=1} \frac{\partial E}{\partial q_{k}} v_{kj} \)
よって、 \( \boldsymbol{U} = ( \boldsymbol{u_1}, \boldsymbol{u_2}, \cdots, \boldsymbol{u_L} )^\mathsf{T}, \boldsymbol{d} = (d_1,d_2,\cdots,d_L), \boldsymbol{V} = ( \boldsymbol{v_1}, \boldsymbol{v_2}, \cdots, \boldsymbol{v_K} )^\mathsf{T}, \boldsymbol{c} = (c_1,c_2,\cdots,c_K), \boldsymbol{W} = ( \boldsymbol{w_1}, \boldsymbol{w_2}, \cdots, \boldsymbol{w_J} )^\mathsf{T}, \boldsymbol{b} = (b_1,b_2,\cdots,b_J) \)の勾配は次のように求まります。
\( \boldsymbol{U}^{(i+1)} \)
\( \quad=\boldsymbol{U}^{(j)}+\eta \frac{1}{N} \sum^{N}_{n=1} ( \boldsymbol{t_{n}}-\boldsymbol{y_{n}}) \boldsymbol{h_{(2)}} \)
\( \boldsymbol{d}^{(i+1)} \)
\( \quad=\boldsymbol{d}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} ( \boldsymbol{t_{n}}-\boldsymbol{y_{n}}) \)
\( \boldsymbol{V}^{(i+1)} \)
\( \quad=\boldsymbol{V}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} \frac{\partial E}{\partial V} \)
\( \quad=\boldsymbol{V}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} \begin{pmatrix} dv_{11} & \cdots & dv_{1j} & \cdots & dv_{1J} \\ \vdots \\ dv_{k1} & \cdots & dv_{kj} & \cdots & dv_{kJ} \\ \vdots \\ dv_{K1} & \cdots & dv_{Kj} & \cdots & dv_{KJ} \end{pmatrix} \)
\( \quad=\boldsymbol{V}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} \begin{pmatrix} d\boldsymbol{v_{1}} \\ \vdots \\ d\boldsymbol{v_{k}} \\ \vdots \\ d\boldsymbol{v_{K}} \end{pmatrix} \)
\( \quad=\boldsymbol{K}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} \begin{pmatrix} \frac{\partial E}{\partial q_{1}} \\ \vdots \\ \frac{\partial E}{\partial q_{k}} \\ \vdots \\ \frac{\partial E}{\partial q_{K}} \end{pmatrix} \boldsymbol{h_{(1)}}^\mathsf{T}\)
\( \quad=\boldsymbol{V}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} \begin{pmatrix} f(q_{1})(1-f(q_{1})) \sum^{L}_{l=1} \frac{\partial E}{\partial r_{l}} u_{l1} \\ \vdots \\ f(q_{k})(1-f(q_{k})) \sum^{L}_{l=1} \frac{\partial E}{\partial r_{l}} u_{lk} \\ \vdots \\ f(q_{K})(1-f(q_{K})) \sum^{L}_{l=1} \frac{\partial E}{\partial r_{l}} u_{lK} \end{pmatrix} \boldsymbol{h_{(1)}}^\mathsf{T} \)
\( \quad=\boldsymbol{V}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} f(\boldsymbol{q})(\boldsymbol{I}-f(\boldsymbol{q})) \odot \boldsymbol{U}^\mathsf{T} \begin{pmatrix} \frac{\partial E}{\partial r_{1}} \\ \vdots \\ \frac{\partial E}{\partial r_{l}} \\ \vdots \\ \frac{\partial E}{\partial r_{L}} \end{pmatrix} \boldsymbol{h_{(1)}}^\mathsf{T} \)
\( \boldsymbol{c}^{(i+1)} \)
\( \quad=\boldsymbol{c}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} f(\boldsymbol{q})(\boldsymbol{I}-f(\boldsymbol{q})) \boldsymbol{U}^\mathsf{T} \begin{pmatrix} \frac{\partial E}{\partial r_{1}} \\ \vdots \\ \frac{\partial E}{\partial r_{l}} \\ \vdots \\ \frac{\partial E}{\partial r_{L}} \end{pmatrix} \boldsymbol{h_{(1)}}^\mathsf{T} \)
\( \boldsymbol{W}^{(i+1)} \)
\( \quad=\boldsymbol{W}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} \frac{\partial E}{\partial W} \)
\( \quad=\boldsymbol{W}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} \begin{pmatrix} dw_{11} & \cdots & dw_{1m} & \cdots & dw_{1M} \\ \vdots \\ dw_{j1} & \cdots & dw_{jm} & \cdots & dw_{jM} \\ \vdots \\ dw_{J1} & \cdots & dw_{Jm} & \cdots & dw_{JM} \end{pmatrix} \)
\( \quad=\boldsymbol{W}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} \begin{pmatrix} d\boldsymbol{w_{1}} \\ \vdots \\ d\boldsymbol{w_{j}} \\ \vdots \\ d\boldsymbol{w_{J}} \end{pmatrix} \)
\( \quad=\boldsymbol{W}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} \begin{pmatrix} \frac{\partial E}{\partial p_{1}} \\ \vdots \\ \frac{\partial E}{\partial p_{j}} \\ \vdots \\ \frac{\partial E}{\partial p_{J}} \end{pmatrix} \boldsymbol{x}^\mathsf{T}\)
\( \quad=\boldsymbol{W}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} \begin{pmatrix} f(p_{1})(1-f(p_{1})) \sum^{K}_{k=1} \frac{\partial E}{\partial q_{k}} v_{k1} \\ \vdots \\ f(p_{j})(1-f(p_{j})) \sum^{K}_{k=1} \frac{\partial E}{\partial q_{k}} v_{kj} \\ \vdots \\ f(p_{J})(1-f(p_{J})) \sum^{K}_{k=1} \frac{\partial E}{\partial q_{k}} v_{kJ} \end{pmatrix} \boldsymbol{x}^\mathsf{T} \)
\( \quad=\boldsymbol{W}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} f(\boldsymbol{p})(\boldsymbol{I}-f(\boldsymbol{p})) \odot \boldsymbol{V}^\mathsf{T} \begin{pmatrix} \frac{\partial E}{\partial q_{1}} \\ \vdots \\ \frac{\partial E}{\partial q_{k}} \\ \vdots \\ \frac{\partial E}{\partial q_{K}} \end{pmatrix} \boldsymbol{x}^\mathsf{T} \)
\( \boldsymbol{b}^{(i+1)} \)
\( \quad=\boldsymbol{b}^{(i)}+\eta \frac{1}{N} \sum^{N}_{n=1} f(\boldsymbol{p})(\boldsymbol{I}-f(\boldsymbol{p})) \odot \boldsymbol{V}^\mathsf{T} \begin{pmatrix} \frac{\partial E}{\partial q_{1}} \\ \vdots \\ \frac{\partial E}{\partial q_{k}} \\ \vdots \\ \frac{\partial E}{\partial q_{K}} \end{pmatrix} \)
・③確率的勾配降下法
\( \boldsymbol{U}^{(i+1)} \)
\( \quad=\boldsymbol{U}^{(i)}+\eta ( \boldsymbol{t_{n}}-\boldsymbol{y_{n}}) \boldsymbol{h_{(2)}} \)
\( \boldsymbol{d}^{(i+1)} \)
\( \quad=\boldsymbol{d}^{(i)} +\eta ( \boldsymbol{t_{n}}-\boldsymbol{y_{n}}) \)
\( \boldsymbol{V}^{(i+1)} \)
\( \quad=\boldsymbol{V}^{(i)}+\eta f(\boldsymbol{q})(\boldsymbol{I}-f(\boldsymbol{q})) \odot \boldsymbol{U}^\mathsf{T} \begin{pmatrix} \frac{\partial E}{\partial r_{1}} \\ \vdots \\ \frac{\partial E}{\partial r_{l}} \\ \vdots \\ \frac{\partial E}{\partial r_{L}} \end{pmatrix} \boldsymbol{h_{(1)}}^\mathsf{T} \)
(図132)

\( \boldsymbol{c}^{(i+1)} \)
\( \quad=\boldsymbol{c}^{(i)} +\eta f(\boldsymbol{q})(\boldsymbol{I}-f(\boldsymbol{q})) \odot \boldsymbol{U}^\mathsf{T} \begin{pmatrix} \frac{\partial E}{\partial r_{1}} \\ \vdots \\ \frac{\partial E}{\partial r_{l}} \\ \vdots \\ \frac{\partial E}{\partial r_{L}} \end{pmatrix} \)
\( \boldsymbol{W}^{(i+1)} \)
\( \quad=\boldsymbol{W}^{(i)}+\eta f(\boldsymbol{p})(\boldsymbol{I}-f(\boldsymbol{p})) \odot \boldsymbol{V}^\mathsf{T} \begin{pmatrix} \frac{\partial E}{\partial q_{1}} \\ \vdots \\ \frac{\partial E}{\partial q_{k}} \\ \vdots \\ \frac{\partial E}{\partial q_{K}} \end{pmatrix} \boldsymbol{x}^\mathsf{T} \)
(図133)
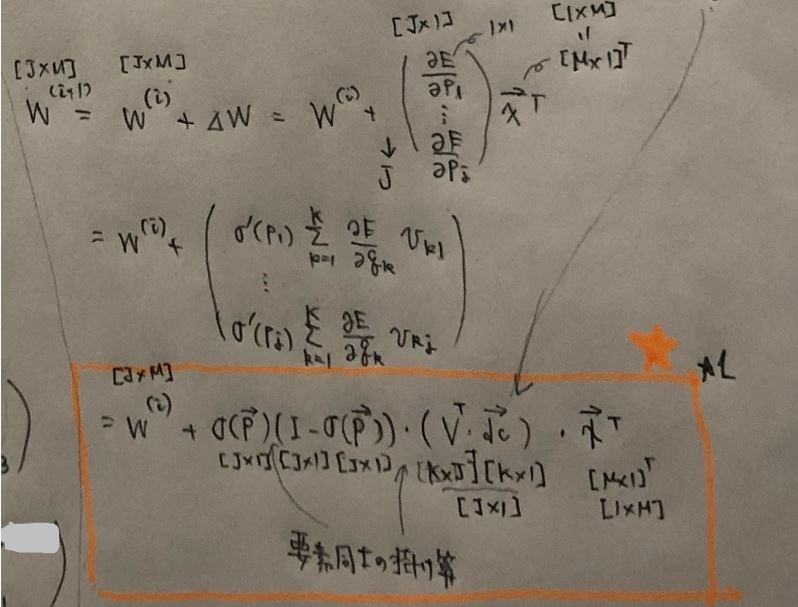
\( \boldsymbol{b}^{(i+1)} \)
\( \quad=\boldsymbol{b}^{(i)} +\eta f(\boldsymbol{p})(\boldsymbol{I}-f(\boldsymbol{p})) \odot \boldsymbol{V}^\mathsf{T} \begin{pmatrix} \frac{\partial E}{\partial q_{1}} \\ \vdots \\ \frac{\partial E}{\partial q_{k}} \\ \vdots \\ \frac{\partial E}{\partial q_{K}} \end{pmatrix} \)
●STEP5:尤度関数の最大値(=傾き0=偏微分が0)を求める【Excel】
→繰り返しにより求める
(参考)
尤度関数や最尤推定の考え方や内容を知りたい方は、下記記事も併せてご覧ください。
⇒参考①:最尤推定とは?考え方を実世界の例も交えシンプルにご紹介
⇒参考②:確率と尤度の違いとは?概念や数式なども交えて比較紹介
⇒参考③:最尤推定の計算を正規分布で行った例をご紹介
>目次にもどる
【オマケ】多層パーセプトロンをExcelで計算
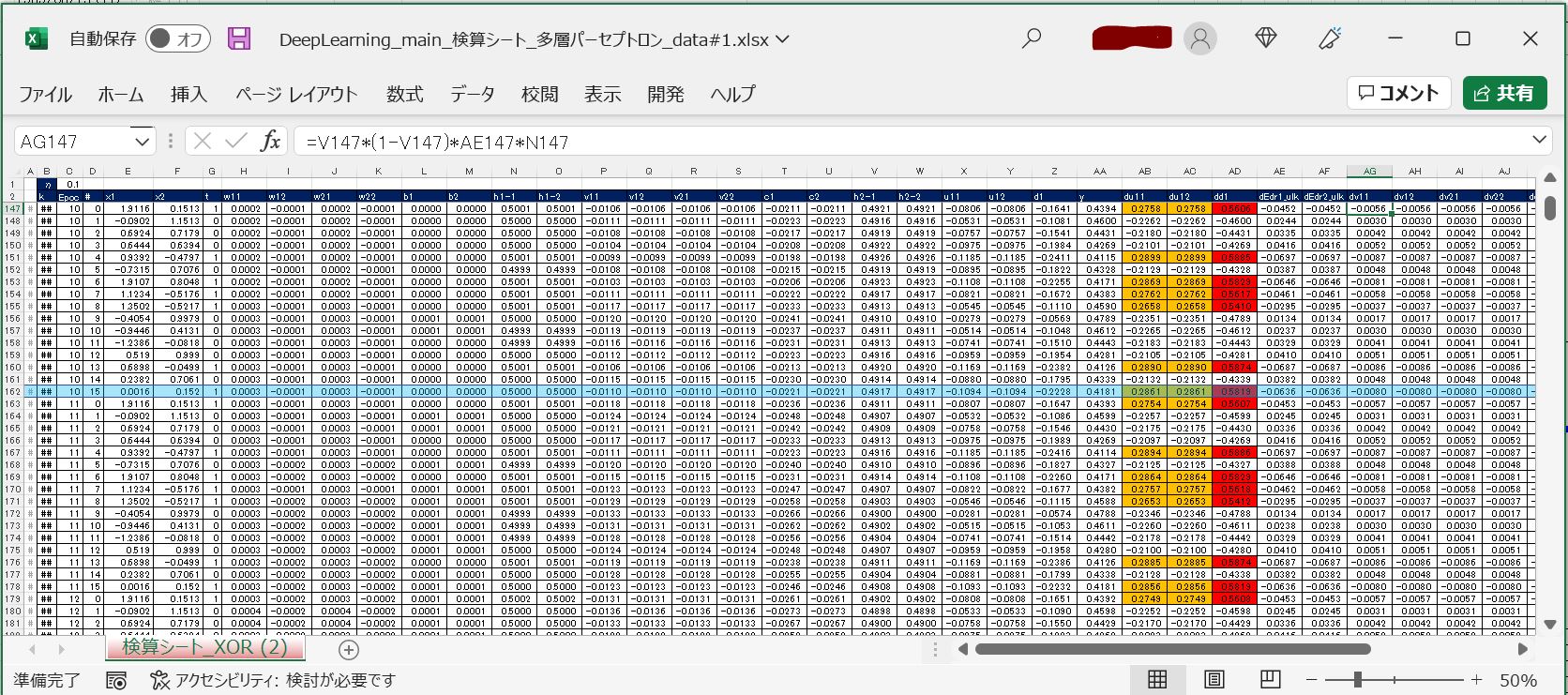
上記で【Excel】印を付けた部分について、Excel上で計算したファイルを添付します。検算等にご活用ください。
⇒実物Excelファイル:DeepLearning_main_検算シート_多層パーセプトロン_data#1
(図141)
>目次にもどる