＜目次＞
多層パーセプトロンをPythonで実装した例をご紹介
(１-１) 実装のフロー
(１-２) サンプルプログラム
多層パーセプトロンをPythonで実装した例をご紹介
多層パーセプトロンについて、Pythonで実装したサンプルプログラムをご紹介します。
多層パーセプトロン（MLP）は、複雑な問題を解くために、パーセプトロン（簡単な判断をする仕組み）を何層にも重ねたものです。入力された情報を「入力層 → 隠れ層 → 出力層」と通して処理し、最終的な答えを出します。これにより、単純なルールだけでなく、画像や音声のような複雑なパターンも学習・分類できます。
多層パーセプトロンを実装する際のポイント（実装のステップ）と、Pythonで実装したサンプルコードをご紹介します。
※多クラス分類のロジスティクス回帰とは？について知りたい方はこちらもご覧ください。
(１-１) 実装のフロー
●STEP0：モデル基本情報
・入力層x＝[M]行
・隠れ層h＝[J]行
・出力層y＝[K]行
・入力データ総数＝[N]
（図１００）
\r\n
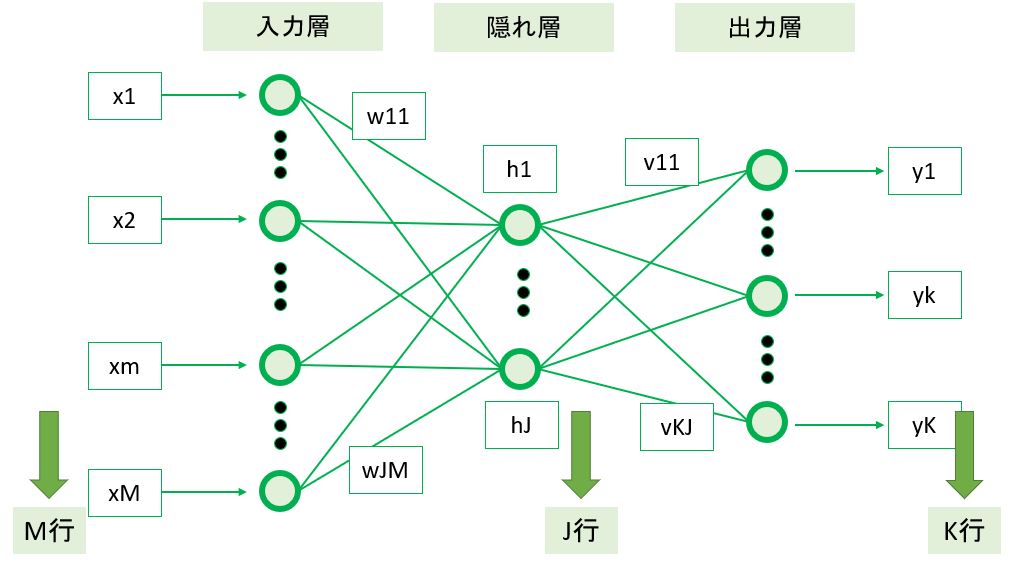\r\n＞目次にもどる\r\n
●STEP1：モデルの定義
・入力の電気信号xの初期化
・重みWの定義
・バイアスbの定義
・隠れ層（シグモイド）：h = σ(Wx + b)の定義
・重みVの定義
・バイアスcの定義
・出力層（シグモイド）：y = σ(Vh + c)の定義
・正解値tの定義
・重みWの勾配（∂E(W,V,b,c)/∂W）の定義
・バイアスbの勾配（∂E(W,V,b,c)/∂b）の定義
・重みVの勾配（∂E(W,V,b,c)/∂V）の定義
・バイアスcの勾配（∂E(W,V,b,c)/∂c）の定義
・学習率：ηの定義
↓
●STEP2：誤差関数の定義
・交差エントロピー誤差関数：E(W,V,b,c) = -Σ[n=1…N]Σ[k=1…K]{t_nk*log(y_nk)}
⇒今回は不要（確率的勾配降下法の最終式を使うため、誤差関数Eは計算不要）
↓
●STEP3：最適化手法の定義（例：勾配降下法）
・隠れ層（シグモイド）：h = σ(Wx + b)の計算
・出力層（シグモイド）：y = σ(Vh + c)の計算
・重みVの勾配（∂E(W,V,b,c)/∂V）の計算
・バイアスcの勾配（∂E(W,V,b,c)/∂c）の計算
・重みWの勾配（∂E(W,V,b,c)/∂W）の計算
・バイアスbの勾配（∂E(W,V,b,c)/∂b）の計算
・重みVの再計算
・バイアスcの再計算
・重みWの再計算
・バイアスbの再計算
↓
●STEP4：セッションの初期化
⇒今回は不要（TensorFlow v2以降はSessionを使用しないため）
↓
●STEP5：学習
・ループ変数の範囲で処理を繰り返す。
＞目次にもどる\r\n
(１-２) サンプルプログラム
（サンプルプログラム）
import numpy as np
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
from sklearn.utils import shuffle
import matplotlib.pyplot as plt
# 入力層xの次元
M = 2
# 隠れ層の次元
J = 2
# 出力層yの次元（クラス数）
K = 1
# 入力データセットの総
nc = 4
# 入力データセットの総数
N = nc * K
def multi_layer_perceptron(X_arg,t_arg):
############################################
# STEP1：モデルの定義
############################################
# 入力の電気信号Xの初期化
X = tf.constant(X_arg, dtype = tf.float64, shape=[N,M])
xn = tf.Variable(tf.zeros([M,1],tf.float64),dtype = tf.float64, shape=[M,1])
# 重みWの定義
W = tf.Variable(tf.zeros([J,M],tf.float64), dtype = tf.float64, shape=[J,M])
# バイアスbの定義 （※データはn個でも1つのbを更新）
b = tf.Variable(tf.zeros([J,1],tf.float64), dtype = tf.float64, shape=[J,1])
# 隠れ層の出力（シグモイド関数）：h = σ(Wx + b)の定義 （※データはn個でも1つのyを更新）
h = tf.Variable(tf.zeros([J,1],tf.float64), dtype = tf.float64, shape=[J,1])
# 重みVの定義
V = tf.Variable(tf.zeros([K,J],tf.float64), dtype = tf.float64, shape=[K,J])
# バイアスcの定義 （※データはn個でも1つのbを更新）
c = tf.Variable(tf.zeros([K,1],tf.float64), dtype = tf.float64, shape=[K,1])
# 出力層の出力（ソフトマックス関数）：y = softmax(Vh + c)の定義 （※データはn個でも1つのyを更新）
y = tf.Variable(tf.zeros([K,1],tf.float64), dtype = tf.float64, shape=[K,1])
# 出力層の正解値tの定義
t = tf.Variable(t_arg, dtype = tf.float64, shape=[N,K])
# 重みWの勾配（∂E(W,V,b,c)/∂W）の定義
dW = tf.Variable(tf.zeros([J,M],tf.float64), dtype = tf.float64, shape=[J,M])
# バイアスbの勾配（∂E(W,V,b,c)/∂b）の定義
db = tf.Variable(tf.zeros([J,1],tf.float64), dtype = tf.float64, shape=[J,1])
# 重みVの勾配（∂E(W,V,b,c)/∂V）の定義
dV = tf.Variable(tf.zeros([K,J],tf.float64), dtype = tf.float64, shape=[K,J])
# バイアスcの勾配（∂E(W,V,b,c)/∂c）の定義
dc = tf.Variable(tf.zeros([K,1],tf.float64), dtype = tf.float64, shape=[K,1])
# 学習率ηの定義
eta = 0.1
# Epoc数の定義
epocs = 1000
############################################
# STEP4：セッションの初期化
############################################
# ⇒今回は不要
# （TensorFlow v2以降はSessionを使用しないため）
############################################
# STEP5：学習
############################################
for epoc in range(epocs):
# バッチのデータ数だけ繰り返し
for n in range(N):
# データをシャッフル
#X_,t_ = shuffle(X.numpy(),t.numpy())
X_,t_ = X.numpy(),t.numpy()
# 取り出したX_[n]を転置してxnに格納(Mx1)
xn.assign(tf.transpose([X_[n]]))
############################################
# STEP2：誤差関数の定義
############################################
# ⇒今回は不要
# （確率的勾配降下法の最終式を使うため、誤差関数Eは計算不要）
############################################
# STEP3：最適化手法の定義（例：勾配降下法）
############################################
# 隠れ層の出力（シグモイド関数）：h = σ(wx + b)の計算
# h[J,1] = sigmoid( W[J×M] × X[M×1] + b[J×1] )
# reshapeで[J]に変換してsigmoidしたのち、再度[J,1]に戻して行列計算できる形に戻す。
h.assign( tf.reshape( tf.nn.sigmoid(tf.reshape(tf.matmul(W,xn)+b,[J])),[J,1]).numpy() )
# 出力層（シグモイド関数）：y = σ(Wx + b)の計算
# y[K,1] = sigmoid( V[K×J] × h[J×1] + c[K×1] )
# reshapeで[K]に変換してsigmoidしたのち、再度[K,1]に戻して行列計算できる形に戻す。
y.assign( tf.reshape( tf.nn.sigmoid(tf.reshape(tf.matmul(V,h)+c,[K])),[K,1]).numpy() )
# ※出力yが多クラスの場合はsoftmaxを使う
# y[K,1] = softmax( V[K×J] × h[J×1] + c[K×1] )
# reshapeに関しては、softmax関数の引数が[K]の形式でないと適切に動かない為に使用している。
# reshapeで[K]に変換してsoftmaxしたのち、再度[K,1]に戻して行列計算できる形に戻す。
#y.assign( tf.reshape( tf.nn.softmax(tf.reshape(tf.matmul(V,h)+c,[K])),[K,1]).numpy() )
# 重みvの勾配（∂E(W,V,b,c)/∂V）の計算
# δK*h[K,J] = dV[K,J] += ( tn[K×1](転置) - y[K×1] ) × hn[1×J](転置)
dV.assign(tf.matmul((tf.transpose([t_[n]])-y),tf.transpose(h)).numpy())
# バイアスcの勾配（δK[K,1] = ∂E(W,V,b,c)/∂c）の計算
dc.assign( tf.transpose([t_[n]])-y )
# dwj[1,M] += { σ'(pj) × Σ[k=1...K]vkj*δk } * xn
# dwj[1,M] += { σ(pj)*(1 - σ(pj)) × Σ[k=1...K](vkj*δk) } × xn
# dwj[1,M] += { σ(wj*xn+b)[1×1]*( 1[1×1] - σ(wj*xn+b)[1×1]) × Σ[k=1...K](vkj[1×1] * δk[1×1]) } × xn[1×M]
# dW[J,M] += { σ(Wj*xn+b)[J×1]*( I[J×1] - σ(W*xn+b)[J×1]) × (V[J×K](転置) × δK[K×1]) } × xn[1×M]
# dW[J,M] += { sigmoid(W*xn+b)[J×1]*(I[J×1]-sigmoid(W*xn+b)[J×1]) × {matmul(V[J×K](転置),δK[K×1])} } × xn[1×M](転置) (※k=1...K)
# σ(pj)*(1 - σ(pj)) = sigmoid(W*xn+b)[J×1]*(I[J×1]-sigmoid(W*xn+b)[J×1]) ⇒[J×1]
I = tf.Variable(tf.ones([J,1],tf.float64), dtype = tf.float64, shape=[J,1])
dfp = tf.math.multiply( h,(I - h) )
# V[J×K](転置) × δK[K×1] ⇒[J×1]
dEdq_vkj = tf.matmul(tf.transpose(V),dc)
# 重みwの勾配（∂E(W,V,b,c)/∂W）の計算
dW.assign( tf.matmul( tf.math.multiply(dfp,dEdq_vkj),tf.transpose(xn)) )
# バイアスbの勾配（∂E(W,V,b,c)/∂b）の計算
db.assign( tf.math.multiply(dfp,dEdq_vkj) )
# コンソール出力
decimals = 4
print("Epoc= ", epoc+1,
"No. = ", n,
"\r\n\t x1,x2 \t\t=", np.array_repr(np.round(X[n].numpy(),decimals)),
"\r\n\t t \t\t=", np.array_repr(np.round(t[n].numpy(),decimals)),
"\r\n\t w1,w2 \t\t=", np.array_repr(np.round(W.numpy(),decimals)).replace('\n', '').replace(' ', ''),
"\r\n\t b \t\t=", np.array_repr(np.round(b.numpy(),decimals)).replace('\n', '').replace(' ', ''),
"\r\n\t h1,h2 \t\t=", np.array_repr(np.round(h.numpy(),decimals)).replace('\n', '').replace(' ', ''),
"\r\n\t v1,v2 \t\t=", np.array_repr(np.round(V.numpy(),decimals)).replace('\n', '').replace(' ', ''),
"\r\n\t c \t\t=", np.array_repr(np.round(c.numpy(),decimals)).replace('\n', '').replace(' ', ''),
"\r\n\t y \t\t=", np.array_repr(np.round(y.numpy(),decimals)).replace('\n', '').replace(' ', ''),
"\r\n\t dv1,dv2 \t=", np.array_repr(np.round(dV.numpy(),decimals)).replace('\n', '').replace(' ', ''),
"\r\n\t dc \t\t=", np.array_repr(np.round(dc.numpy(),decimals)).replace('\n', '').replace(' ', ''),
"\r\n\t dw1,dw2 \t=", np.array_repr(np.round(dW.numpy(),decimals)).replace('\n', '').replace(' ', ''),
"\r\n\t db \t\t=", np.array_repr(np.round(db.numpy(),decimals)).replace('\n', '').replace(' ', ''),
)
# 重みVの再計算
V.assign_add( tf.math.scalar_mul(eta,dV) )
# バイアスbの再計算
c.assign_add( tf.math.scalar_mul(eta,dc) )
# 重みWの再計算
W.assign_add( tf.math.scalar_mul(eta,dW) )
# バイアスbの再計算
b.assign_add( tf.math.scalar_mul(eta,db) )
def main():
# 初期値を設定し学習実行
# テスト用データセット
X = [[0,0],[0,1],[1,0],[1,1]]
t = [[0],[1],[1],[0]]
multi_layer_perceptron(X,t)
if __name__ == "__main__":
main()
（図１３１）
（例）出力結果
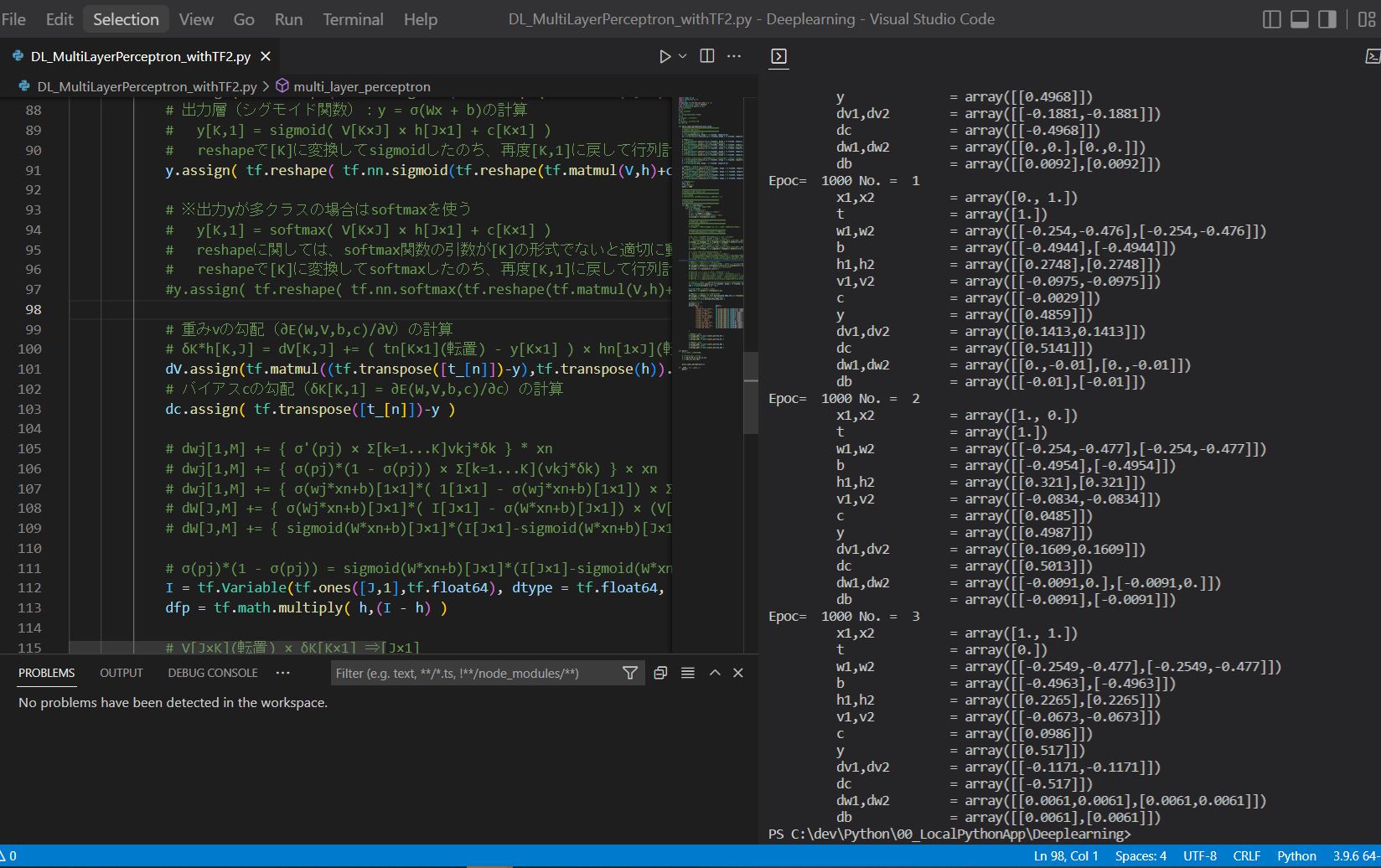
（例）出力結果
Epoc= 1000 No. = 1
x1,x2 = array([0., 1.])
t = array([1.])
w1,w2 = array([[-0.254,-0.476],[-0.254,-0.476]])
b = array([[-0.4944],[-0.4944]])
h1,h2 = array([[0.2748],[0.2748]])
v1,v2 = array([[-0.0975,-0.0975]])
c = array([[-0.0029]])
y = array([[0.4859]])
dv1,dv2 = array([[0.1413,0.1413]])
dc = array([[0.5141]])
dw1,dw2 = array([[0.,-0.01],[0.,-0.01]])
db = array([[-0.01],[-0.01]])
Epoc= 1000 No. = 2
x1,x2 = array([1., 0.])
t = array([1.])
w1,w2 = array([[-0.254,-0.477],[-0.254,-0.477]])
b = array([[-0.4954],[-0.4954]])
h1,h2 = array([[0.321],[0.321]])
v1,v2 = array([[-0.0834,-0.0834]])
c = array([[0.0485]])
y = array([[0.4987]])
dv1,dv2 = array([[0.1609,0.1609]])
dc = array([[0.5013]])
dw1,dw2 = array([[-0.0091,0.],[-0.0091,0.]])
db = array([[-0.0091],[-0.0091]])
Epoc= 1000 No. = 3
x1,x2 = array([1., 1.])
t = array([0.])
w1,w2 = array([[-0.2549,-0.477],[-0.2549,-0.477]])
b = array([[-0.4963],[-0.4963]])
h1,h2 = array([[0.2265],[0.2265]])
v1,v2 = array([[-0.0673,-0.0673]])
c = array([[0.0986]])
y = array([[0.517]])
dv1,dv2 = array([[-0.1171,-0.1171]])
dc = array([[-0.517]])
dw1,dw2 = array([[0.0061,0.0061],[0.0061,0.0061]])
db = array([[0.0061],[0.0061]])
