＜目次＞
(１) tensorflowのmatmulの使い方について（次元別の仕様やnumpy.matmulとの違いを整理）
(１-１) tensorflow.matmulの次元別の挙動
(１-２) tensorflow.matmulの次元別の挙動（詳細）
(１-３) tensorflow.matmulの次元別の挙動確認に使用したプログラム
(１-４) （参考）numpyのmatmulについて
(１) tensorflowのmatmulの使い方について（次元別の仕様やnumpy.matmulとの違いを整理）
(１-１) tensorflow.matmulの次元別の挙動
（表）
| 次元 （行列1＼行列2） |
n=1 | n=2 | n>2 |
| n=1 （例：[1]） |
① ・エラー （In[0] and In[1] ndims must be >= 2） |
② ・エラー （In[0] and In[1] has different ndims: [2] vs. [2,1]） |
③ ・エラー （In[0] ndims must be >= 2） |
| n=2 （例：[[1],[1]]） |
④ ・エラー （In[0] and In[1] has different ndims: [1,2] vs. [2]） |
⑤ ・行列の掛け算 |
⑥ ・最後の2次元の行列をスタックした扱い。 ・掛け算の考え方はブロードキャスト |
| n>2 （例：[[[1],[1]],[[1],[1]]]） |
⑦ ・エラー （In[1] ndims must be >= 2） |
⑧ ・最後の2次元の行列をスタックした扱い。 ・掛け算の考え方はブロードキャスト |
⑨ ・最後の2次元の行列をスタックした扱い。 ・先頭の次元が同じ場合に限り、対応する要素の行列同士を掛け算 |
(１-２) tensorflow.matmulの次元別の挙動（詳細）
●①②③④⑦（第１引数or第２引数のいずれかにN=1を含む）
⇒エラーになる。
⇒ただし、同じmatmulでもnumpy.matmulの場合はN=1の場合、計算時にN=2に補って計算してくれます（例：[2]なら[[2]]に変換して計算）。
●⑤「N=2 & N=2」
⇒行列の計算として扱える
●⑥⑧⑨「N≧2 & N>2」の場合
・numpyドキュメントに以下の記述あり（①②③④⑦以外はnumpyもtensorflowも同一挙動のため参考する）
（図１１１）
↓
・最後の2つの次元（例：2×3×3なら「3×3」の部分）の行列の「スタック」（行列を連結）として扱われます。（例）下図の「赤色の3×3」と「緑色の3×3」の2行列が連結された形です。
（図１２０）
↓
・基本的に、対応する要素同士（赤同士、緑同士）を掛け算します（先頭の次元が同じ数字の場合に限る。
⇒（例）2×3×3と3×3×3は掛け合わせ不可
⇒「⑨」に該当
（図１２１）
↓
・ただし、先頭の次元が1の場合（例：1×3×3）の場合は、ブロードキャストされます
⇒（例）行列a_1x2x2の2×2を、行列b_2x2x2の2×2（２個）のそれぞれと掛け合わせ）
⇒「⑥」「⑧」に該当
（図１２２）
↓
・⑥例：a_2d_1x2の「1×2」を、a_3d_2x2x1の「2×1」（２個）と掛け合わせ
・⑧例：a_3d_2x2x1の「2×1」（２個）を、a_2d_1x2の「1×2」と掛け合わせ
・⑨例：a_3d_2x2x1の「2×1」（２個）を、a_3d_2x1x2の「1×2」（２個）と掛け合わせ（対応する行列同士）
（図１３１）
↓
・今までの説明で確認した法則に則っている事を確認
（図１３２）
↓
・⑨補足
「対応する行列同士」が「赤同士、緑同士」である事を実証するため、次の簡単な確認を実施。
⇒図の中段：緑の行列の最後を[1,2,4]に変更すると、緑の行列にのみ影響（最後が[7,7,7]に変化）
⇒図の下段：赤の行列の最後を[1,1,2]に変更すると、緑の行列にのみ影響（最後が7] 7] 7]に変化）
（図１３４）
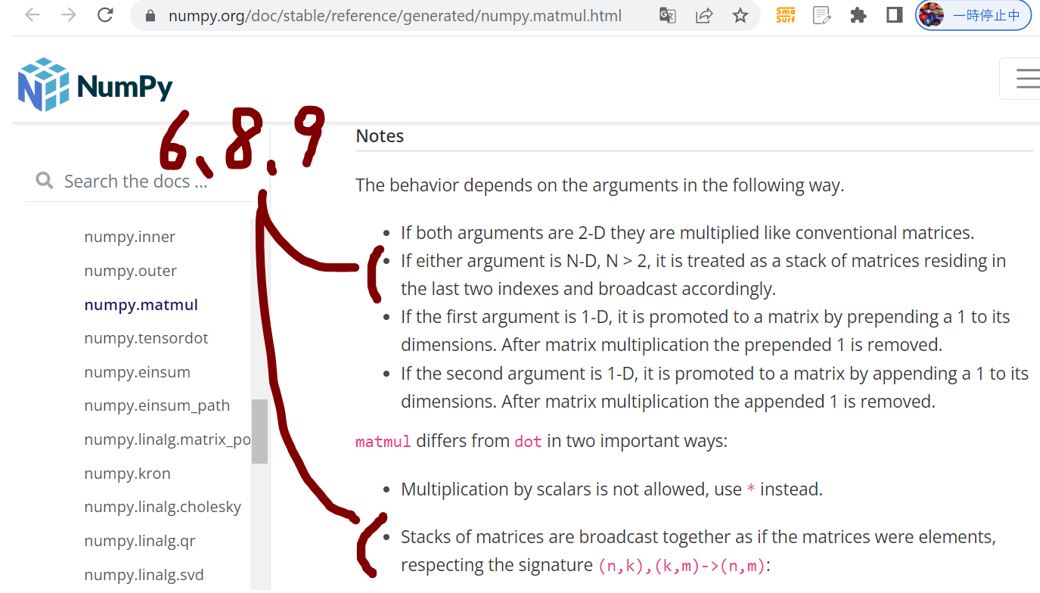
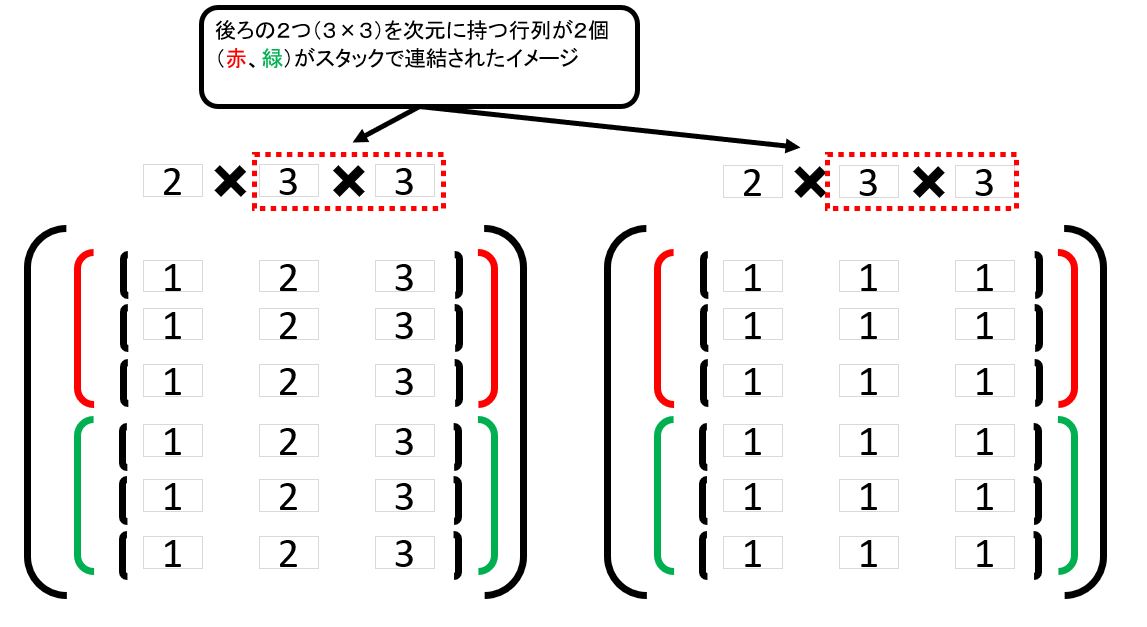
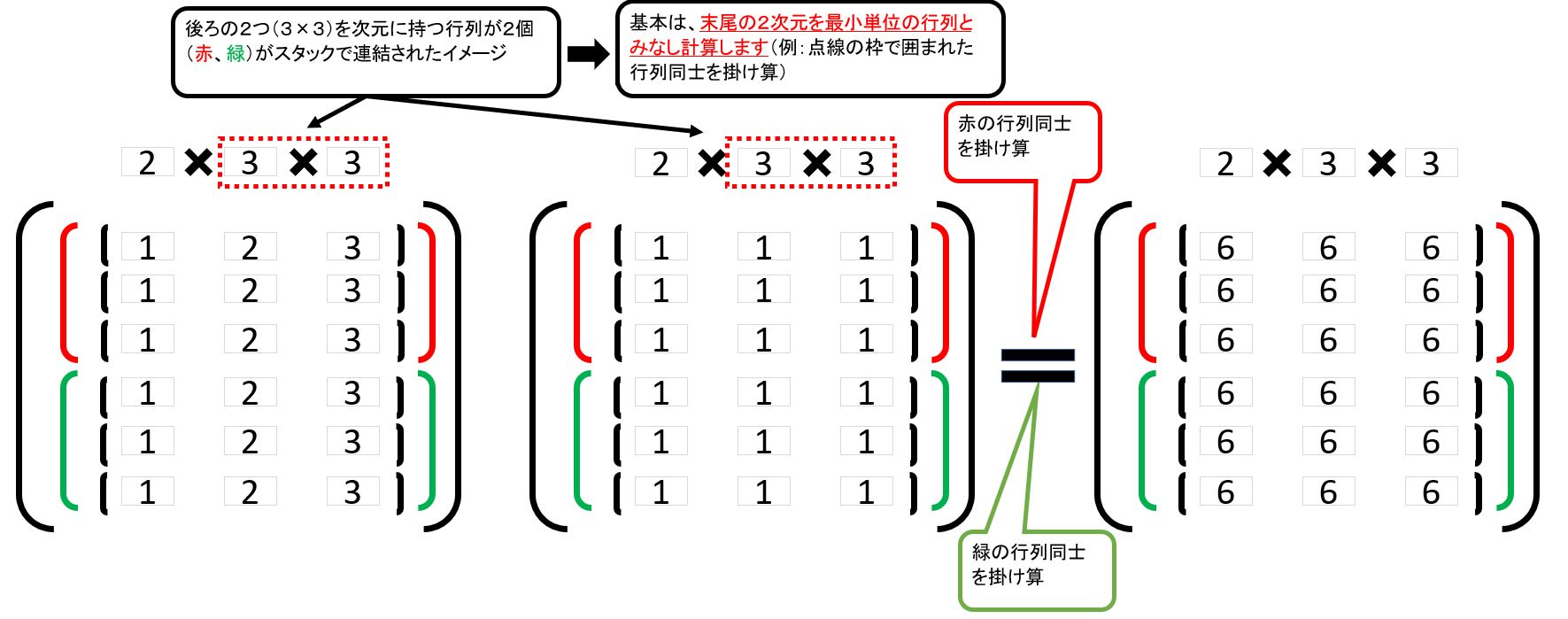
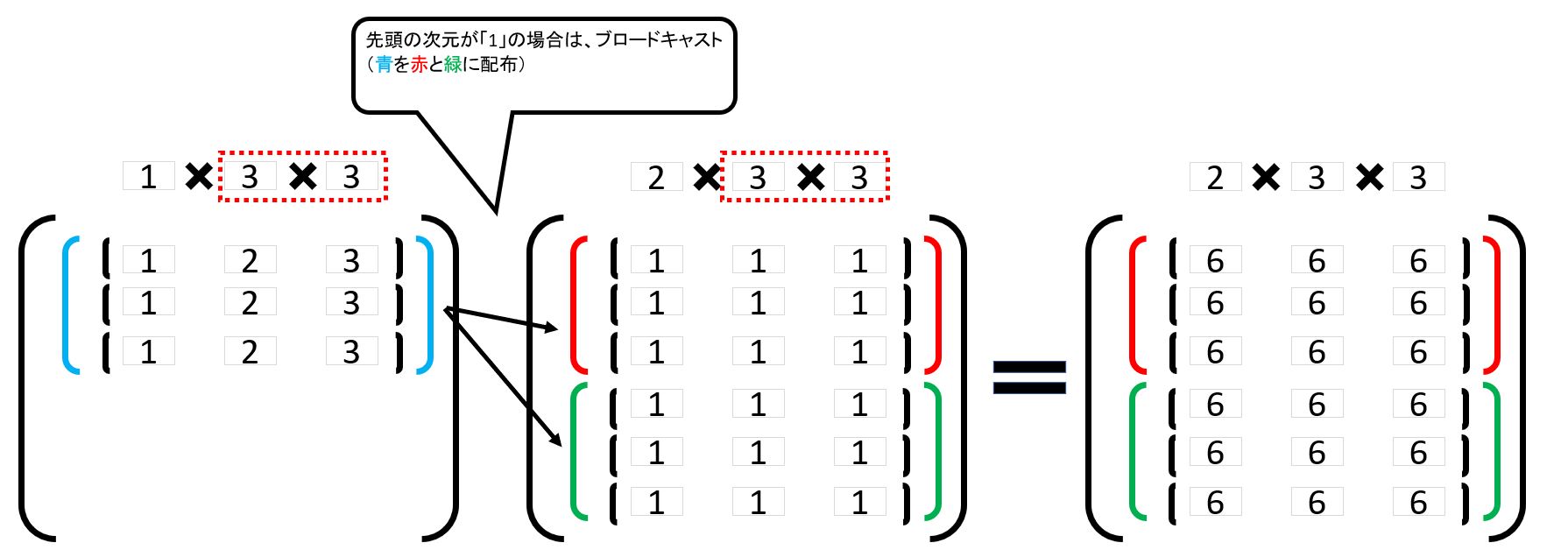
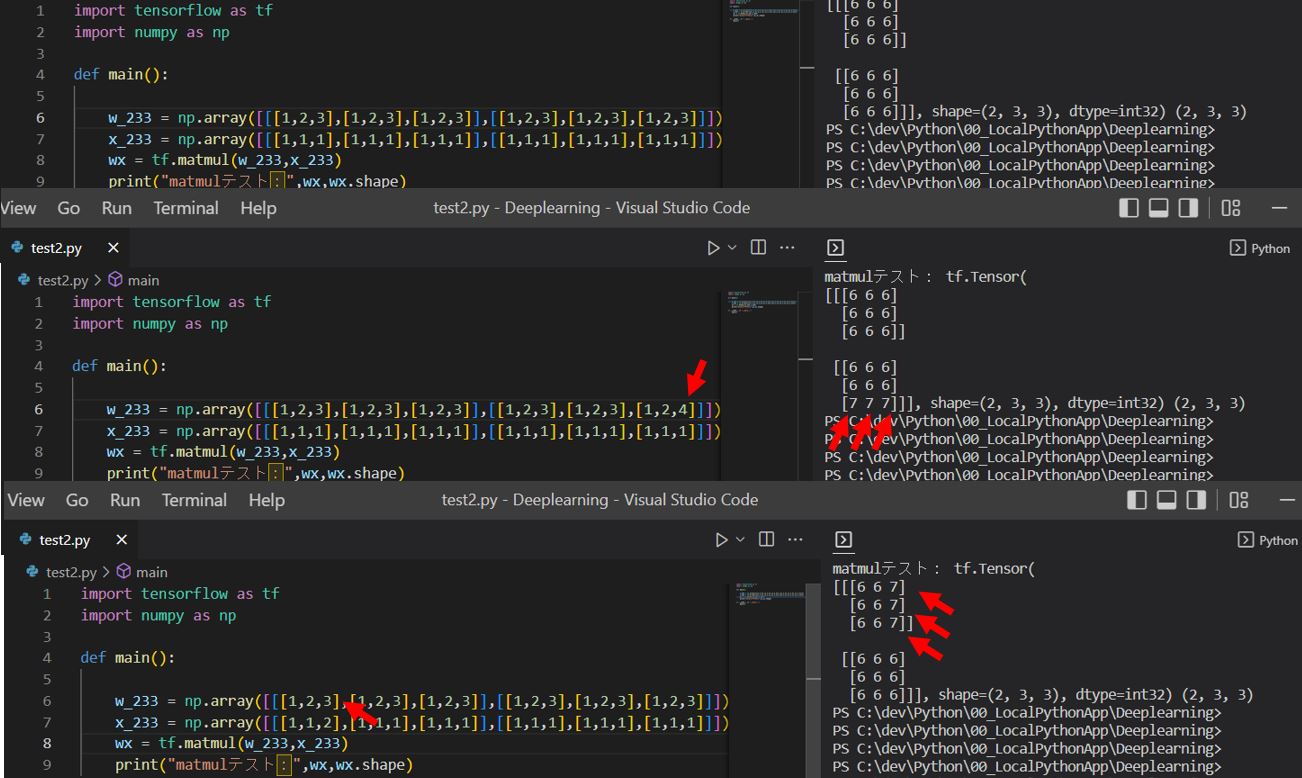
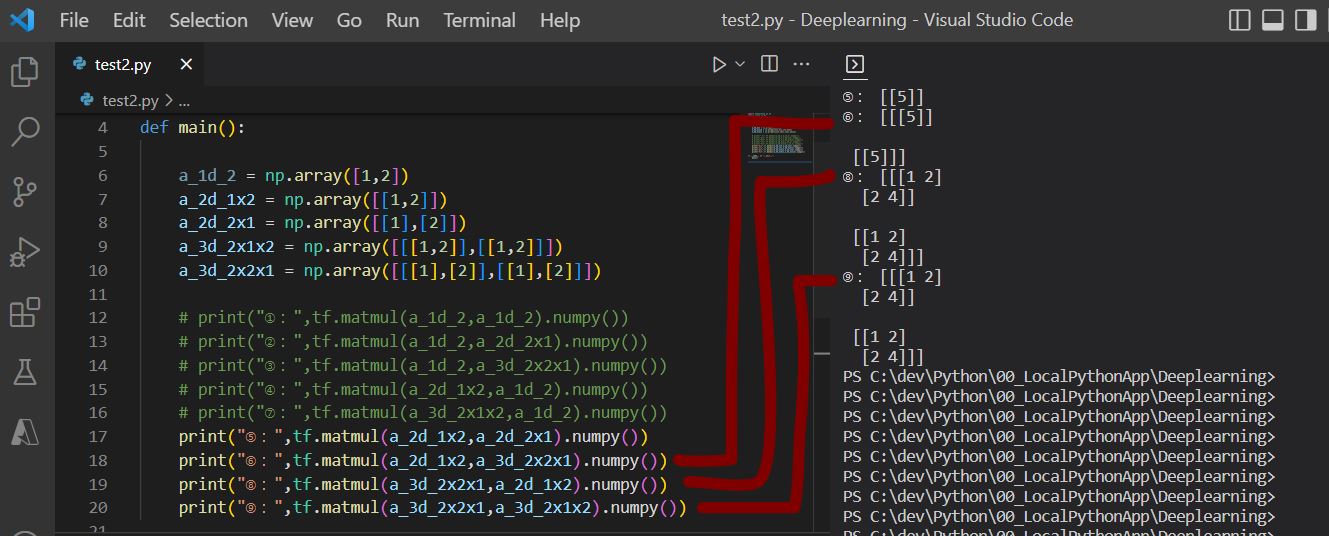
(１-３) tensorflow.matmulの次元別の挙動確認に使用したプログラム
（テストコード）
import tensorflow as tf
import numpy as np
def main():
a_1d_2 = np.array([1,2])
a_2d_1x2 = np.array([[1,2]])
a_2d_2x1 = np.array([[1],[2]])
a_3d_2x1x2 = np.array([[[1,2]],[[1,2]]])
a_3d_2x2x1 = np.array([[[1],[2]],[[1],[2]]])
# print("①：",tf.matmul(a_1d_2,a_1d_2).numpy())
# print("②：",tf.matmul(a_1d_2,a_2d_2x1).numpy())
# print("③：",tf.matmul(a_1d_2,a_3d_2x2x1).numpy())
# print("④：",tf.matmul(a_2d_1x2,a_1d_2).numpy())
# print("⑦：",tf.matmul(a_3d_2x1x2,a_1d_2).numpy())
print("⑤：",tf.matmul(a_2d_1x2,a_2d_2x1).numpy())
print("⑥：",tf.matmul(a_2d_1x2,a_3d_2x2x1).numpy())
print("⑧：",tf.matmul(a_3d_2x2x1,a_2d_1x2).numpy())
print("⑨：",tf.matmul(a_3d_2x2x1,a_3d_2x1x2).numpy())
if __name__ == "__main__":
main()
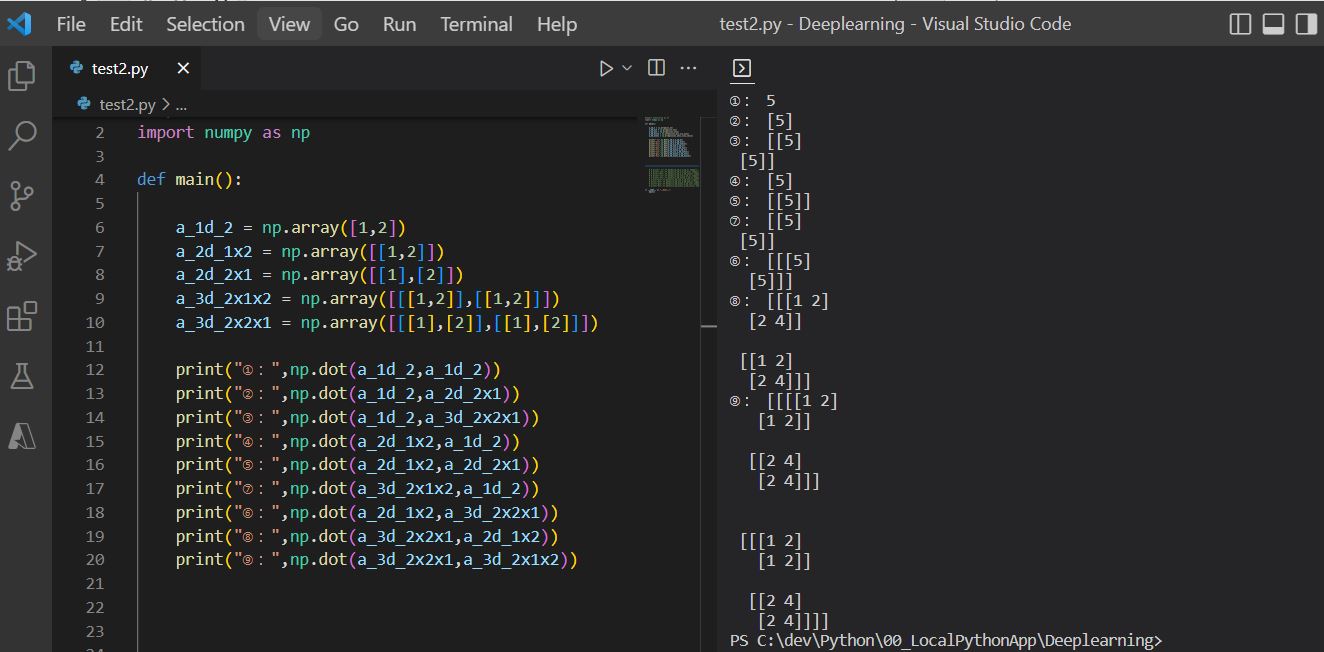
(１-４) （参考）numpyのmatmulについて
・matmulはtensorflowのみならずnumpyにも同一名称の関数がありますが、少し挙動が異なります。
・①②③④⑦はエラーにせず、次元を補う事で内積計算を可能にしています。
（表）
| 次元 （行列1＼行列2） |
n=1 | n=2 | n>2 |
| n=1 （例：[1]） |
① ・ベクトルの内積 |
② ・ベクトルの内積（の繰り返し） ⇒第１引数行列と第２引数列の最初の次元の内積を取る |
③ ・ベクトルの内積（の繰り返し） ⇒第１引数行列と第２引数列の最初の次元の内積を取る |
| n=2 （例：[[1],[1]]） |
④ ・ベクトルの内積（の繰り返し） ⇒第１引数行列の最後の次元と第２引数列の内積を取る |
⑤ ・行列の掛け算 |
⑥ ・最後の2次元の行列をスタックした扱い。 ・掛け算の考え方はブロードキャスト |
| n>2 （例：[[[1],[1]],[[1],[1]]]） |
⑦ ・ベクトルの内積（の繰り返し） ⇒第１引数行列の最後の次元と第２引数列の内積を取る |
⑧ ・最後の2次元の行列をスタックした扱い。 ・掛け算の考え方はブロードキャスト |
⑨ ・最後の2次元の行列をスタックした扱い。 ・先頭の次元が同じ場合に限り、対応する要素の行列同士を掛け算 |
