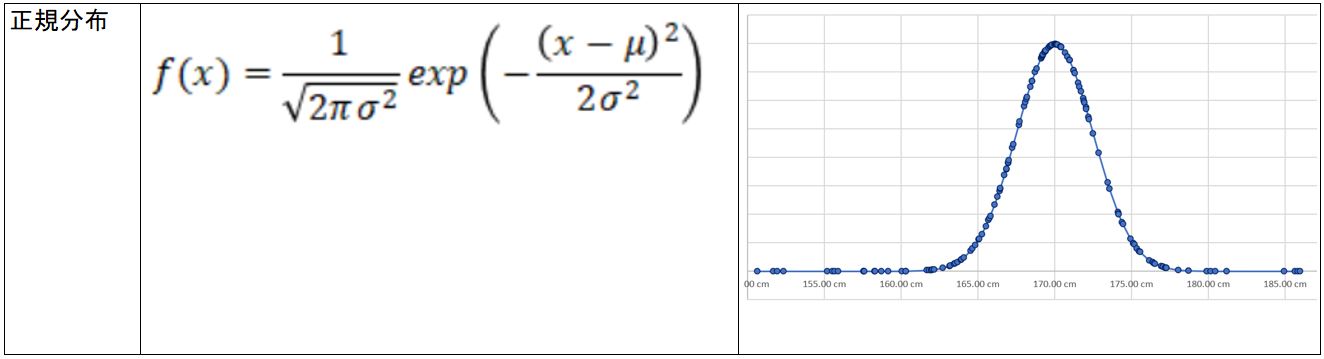<目次>
(1) 最尤推定とは?考え方を実世界の例も交えシンプルにご紹介
(1-1) 最尤推定とは?
(1-2) 最尤推定の考え方
(1-3) 最尤推定の実際の計算方法は?
(1) 最尤推定とは?考え方を実世界の例も交えシンプルにご紹介
(1-1) 最尤推定とは?
・「データ群」(例:身長、体重)に対して、尤もらしい「分布(distribution)」のパラメータを特定するための手法です。
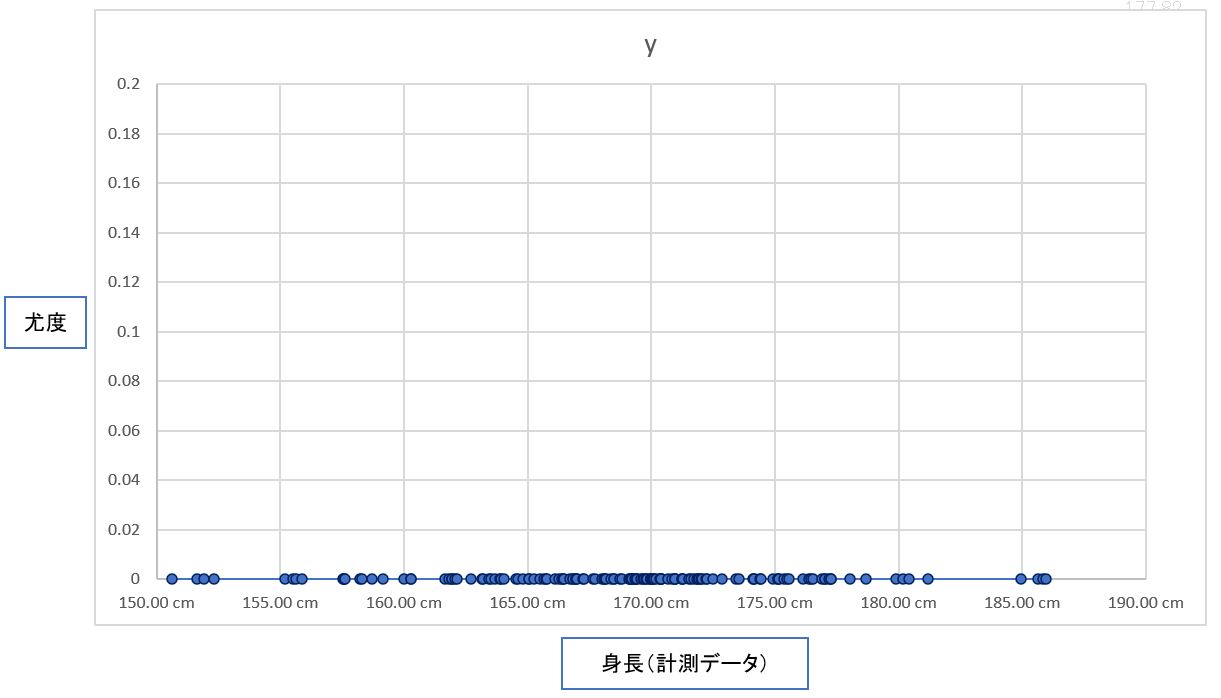
・(例)小学1年生の体重のデータ(150件)から最尤推定を行い、データに適合する確率密度関数(正規分布)のパラメータ(標準偏差σ、平均値μ)を求める。
(図111)
↓
最尤推定を行い、確率密度関数(正規分布)のパラメータ(標準偏差σ、平均値μ)を求める
↓
(図112)
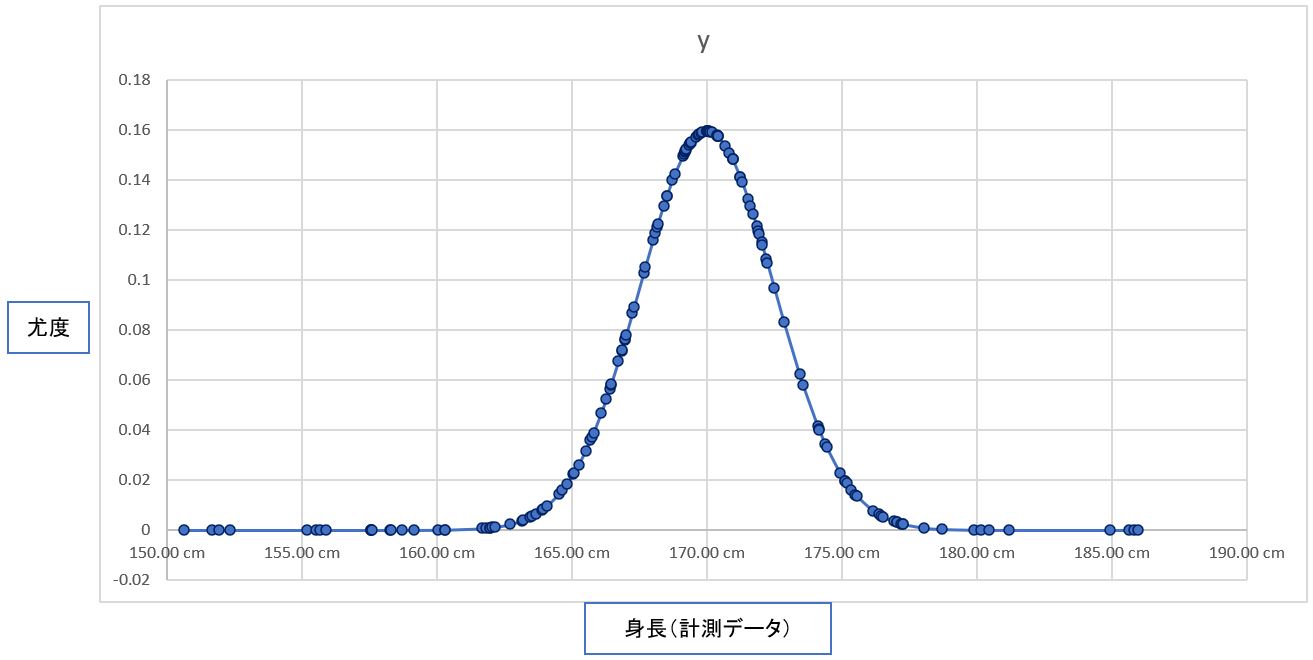
・これはある意味では「確率」の算出とは逆の考え方になります。
・しかし、現実世界を考えてみても、最初から分布(やそのパラメータσ、μ)が分かっている事は少ない。
(図113)どんな分布になるか?はデータを計測してみないと分からない
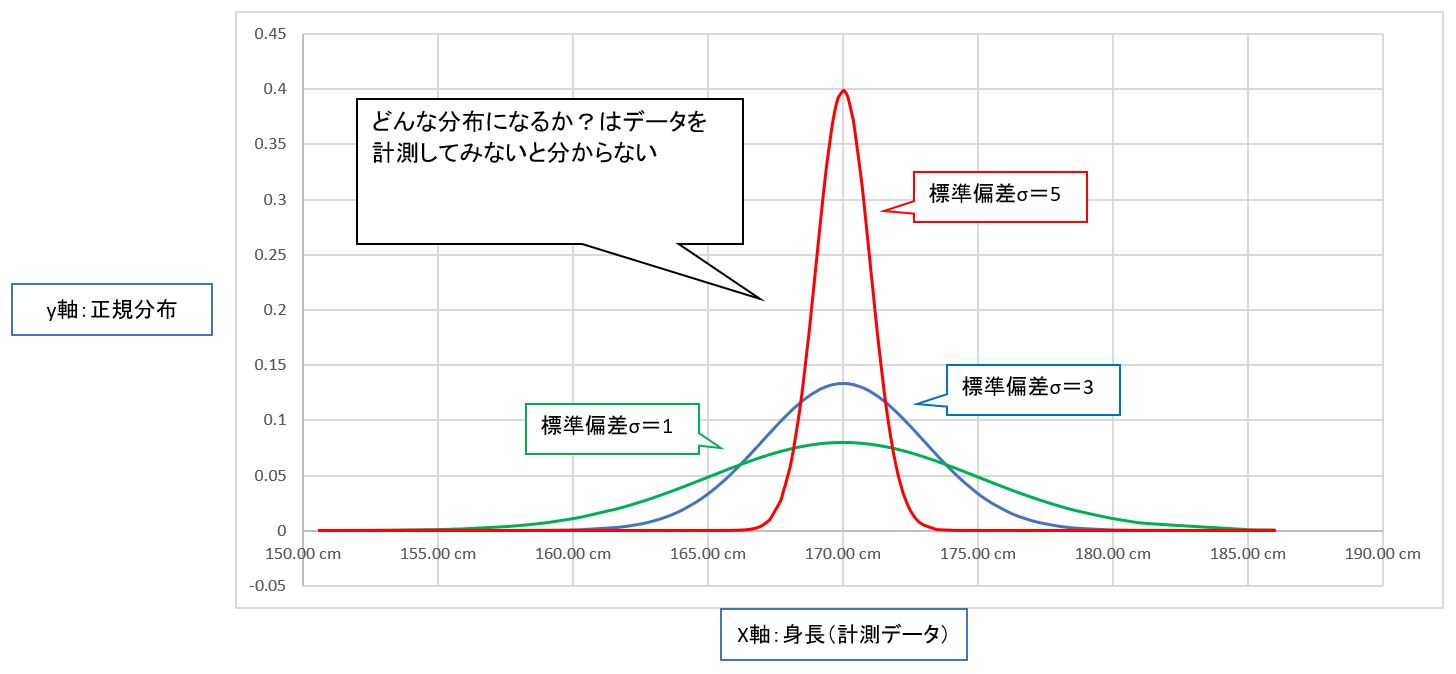
↓
・そのため、まずはデータOを測定して分布を推定(最尤推定)する流れになる
(図114)
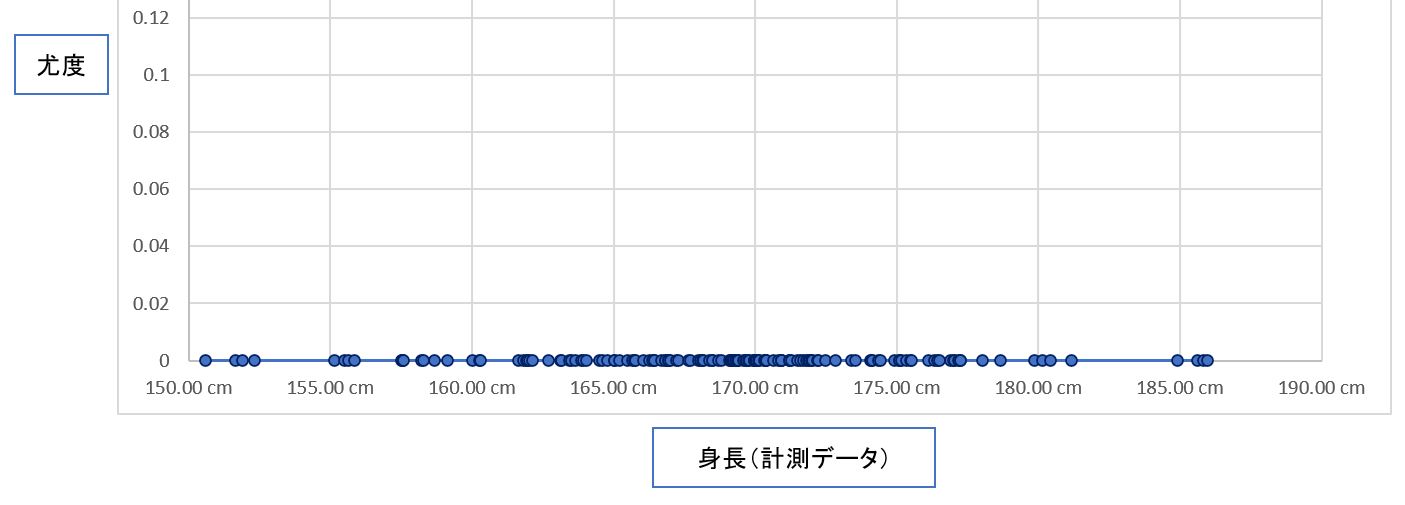
・その際、パラメータ(μ、σ)が与えられた時の確率がP(データO|μ,σ)である。
→逆に、データOを「観測する確率が最も高いパラメータ(μ、σ)」が最適なパラメータである
→このプロセスが最尤推定
(1-2) 最尤推定の考え方
最尤推定の考え方の流れ(アプローチ)を説明します。数学部分を省略しており正確ではありませんが、イメージを掴める事を目的にします。
●STEP1:分布の種類を仮定(例:正規分布)
・①分布には様々な種類があります。例えば、正規分布、指数分布、ガンマ分布など
(図121①)
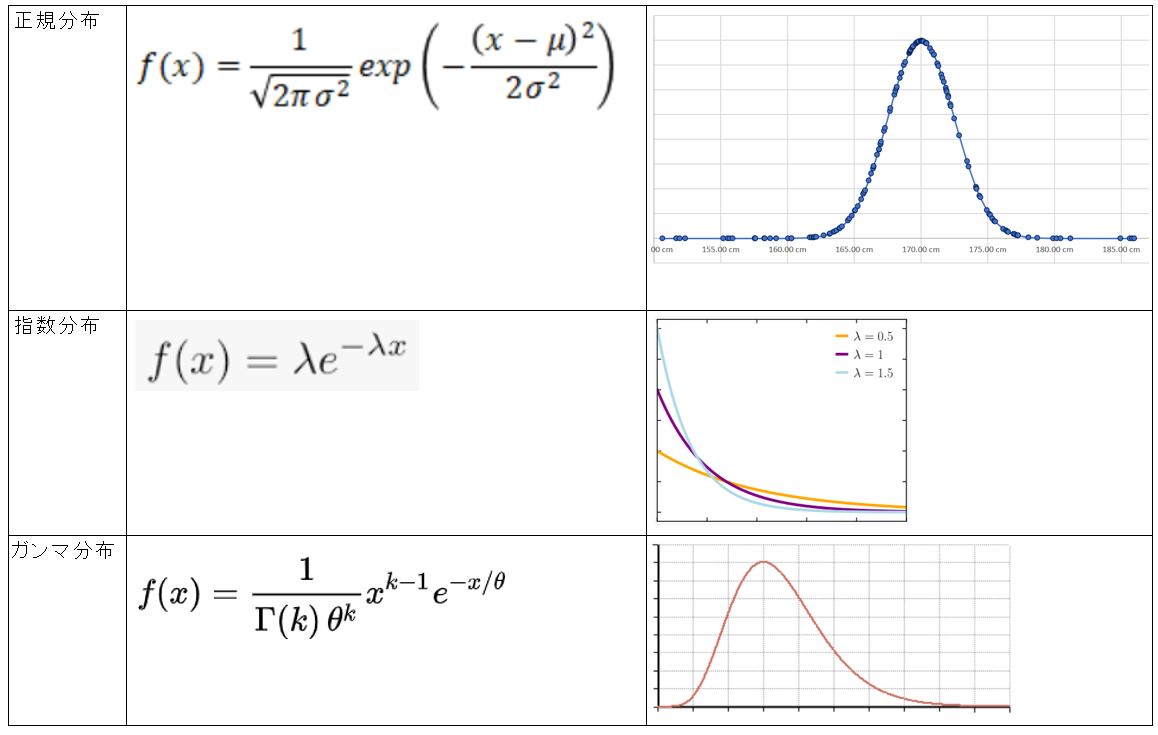
↓
・②その中でも、例えば「体重」という指標の場合は「正規分布」に従うと予想します。
(図121②)
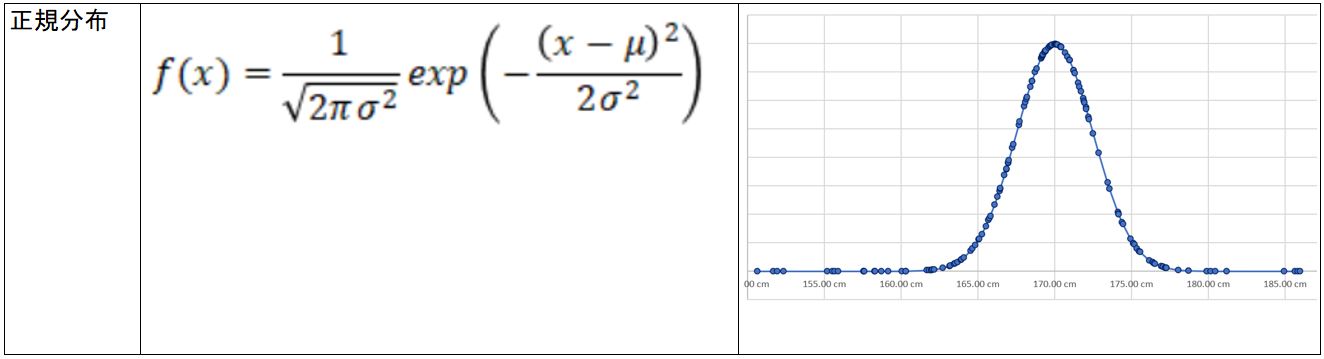
↓
・③仮に「正規分布」である場合、「平均値μ(mean)」に関連した次の特徴があります。
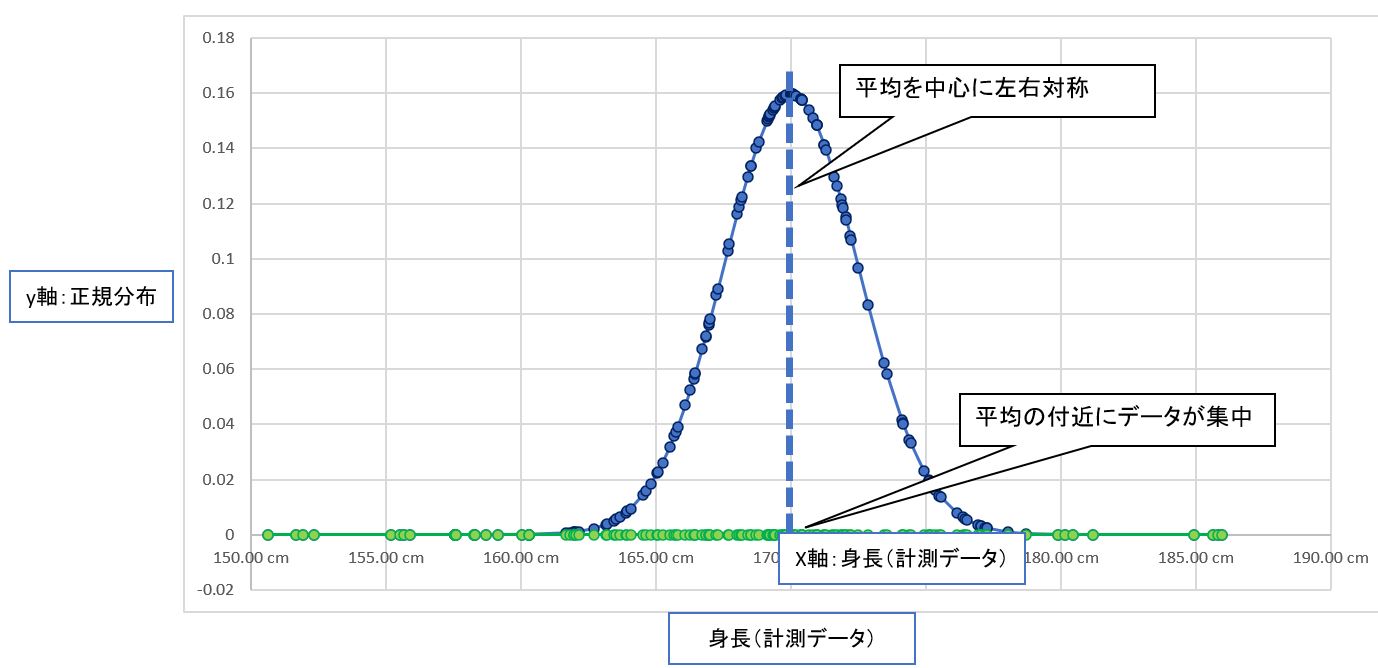
・(1)多くの計測結果(体重)は「平均値μ(mean)」に近い値になる
→データの多くは平均値の近くに集中している
・(2)計測データは平均を中心として、比較的に左右対象になっている
→完全に左右対称ではないものの、極端に偏ったりはしていないはず
(図121③)
●STEP2:片方のパラメータ(標準偏差σ)を固定して「平均値μ」を推定
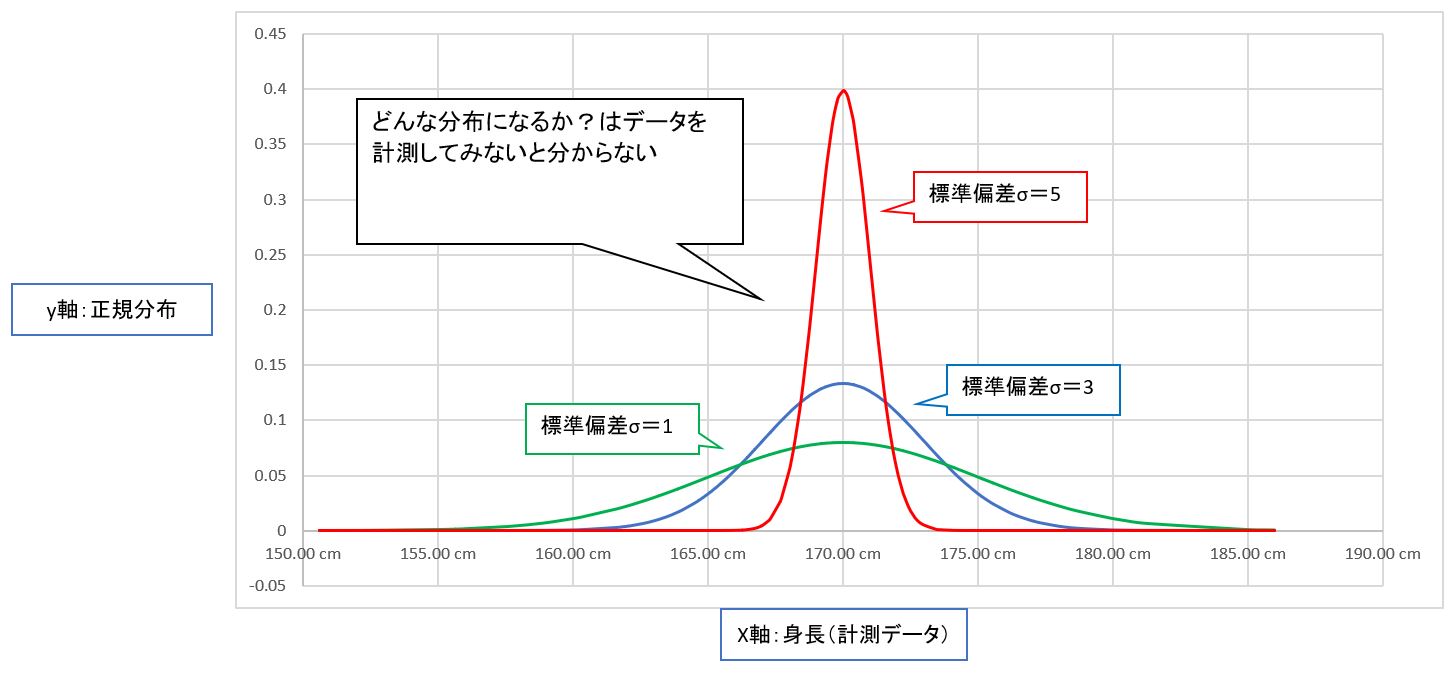
・①更に正規分布には「標準偏差σ」に応じて様々な形になります。
(図122①)
↓
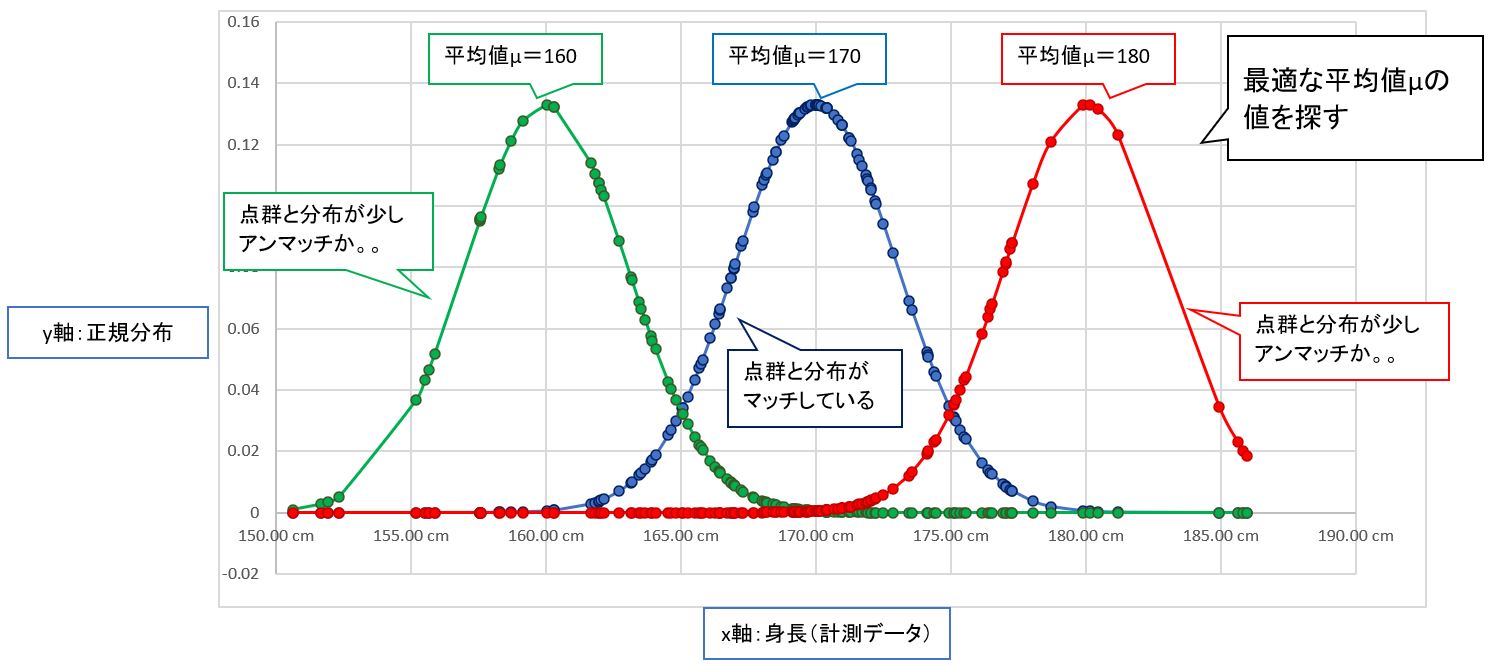
・②分布の形(標準偏差σ)を1つに固定した後に、中央の線(平均値μ)がどこに来るか?を探っていきます。
→平均値μについての「最尤推定」
(図122②)
↓
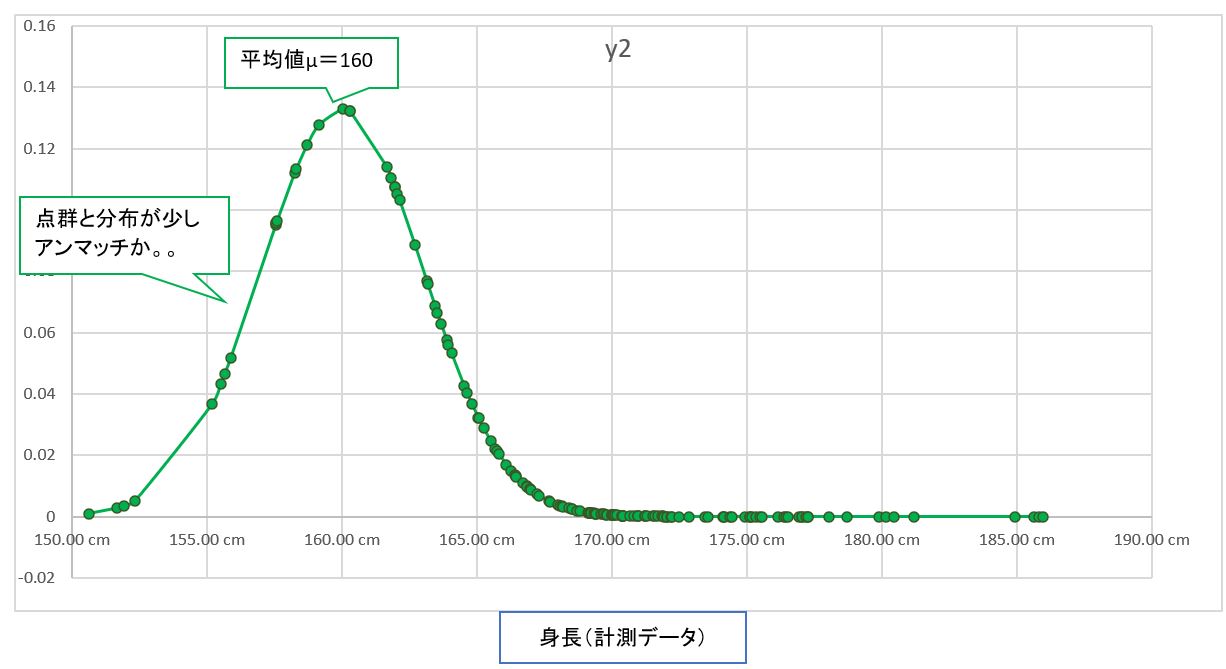
・③例えば、グラフを左側に置いて見ると、どうも分布の中央線(平均値μ)と点群の密集している部分は合致しません。これは「尤度が低い」(尤もらしくない)状態といえます。
(図122③)
↓
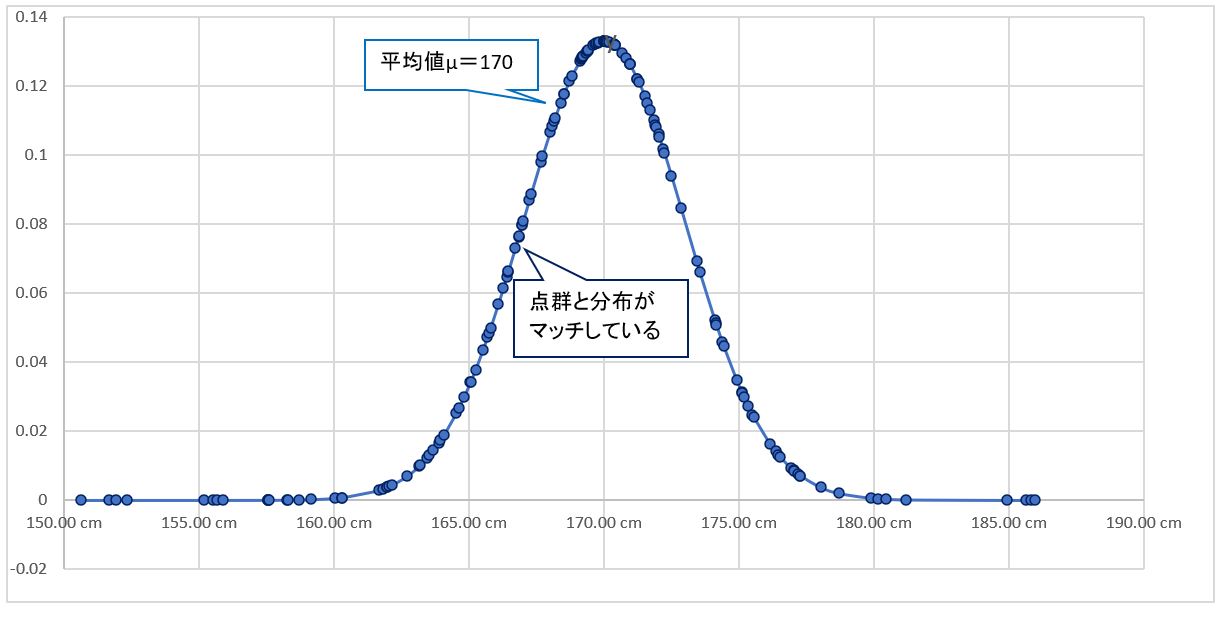
・④一方、グラフを中央に置き、分布の中央線(平均値μ)と点群データの平均が重なる場合は、「尤度が高い」(尤もらしい)状態と言えます。
(図122④)
↓
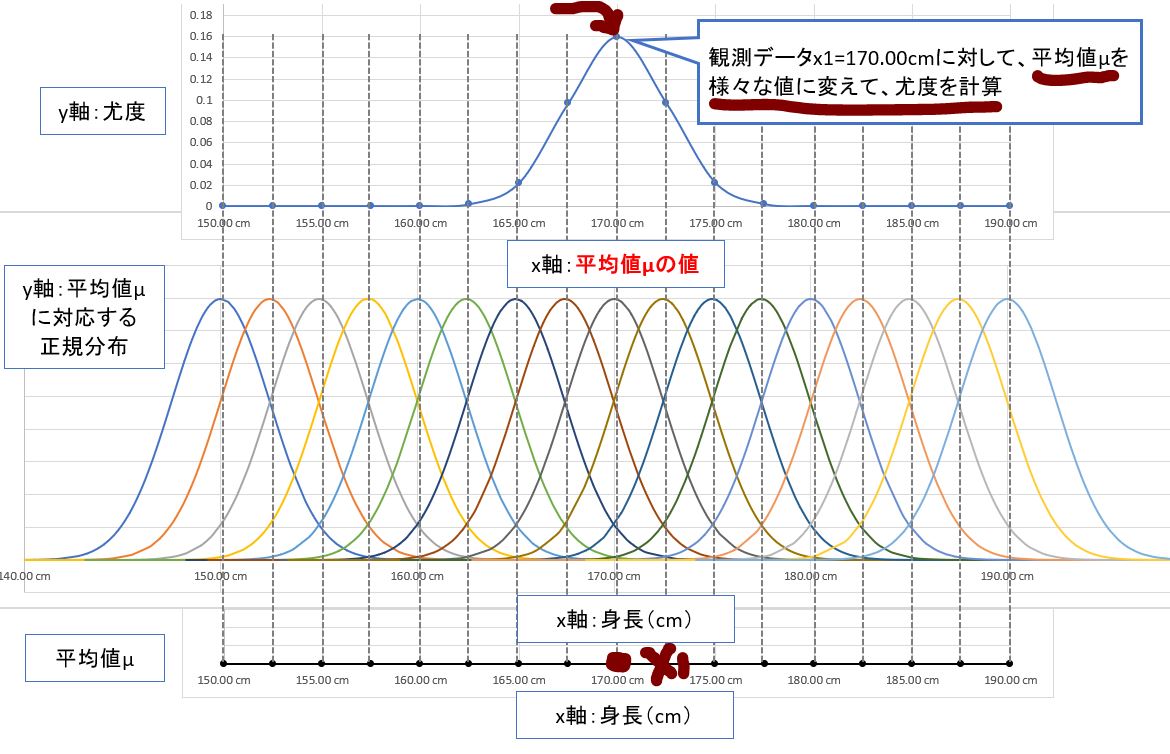
・⑤最尤推定の実行
平均値μ(mean)をずらしながら、その都度「尤度(likelihood)」を計算していく事で、どこかの地点で「尤度」が「最大になる」はずです。
⇒これを割り出すプロセスが「最尤推定」です。
(図122⑤)
(備考①)
今回は「データの平均(mean)」ではなく「分布の平均(mean)」を考えていますが、「正規分布」においては、それら2つは同一となります。
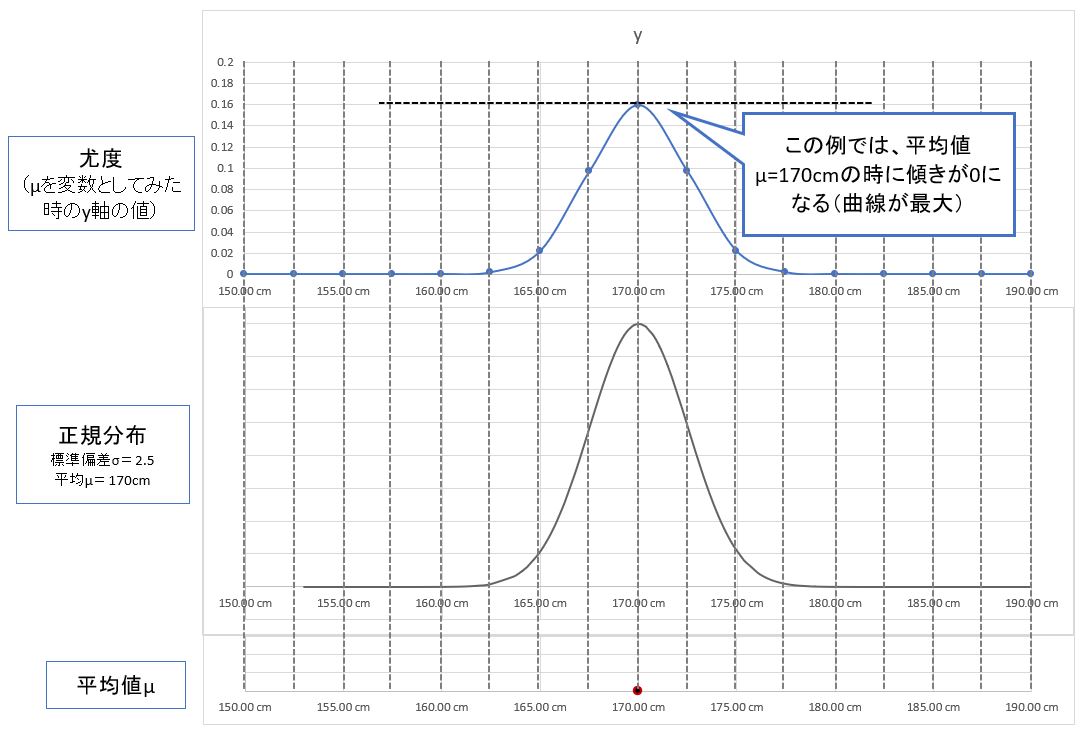
(備考②)
これは数学的には、標準偏差σを定数、平均値μを変数として扱った時の曲線の傾き=0の点(つまり最大)です(=すなわち、μで「偏微分」した時に0になる地点)
(図123)
●STEP3:もう片方のパラメータ(平均値μ)を固定して「標準偏差σ」を推定
・①同様に「標準偏差σ」についても最尤推定を行う
⇒横軸=標準偏差、縦軸=観測データの尤度
(図124)
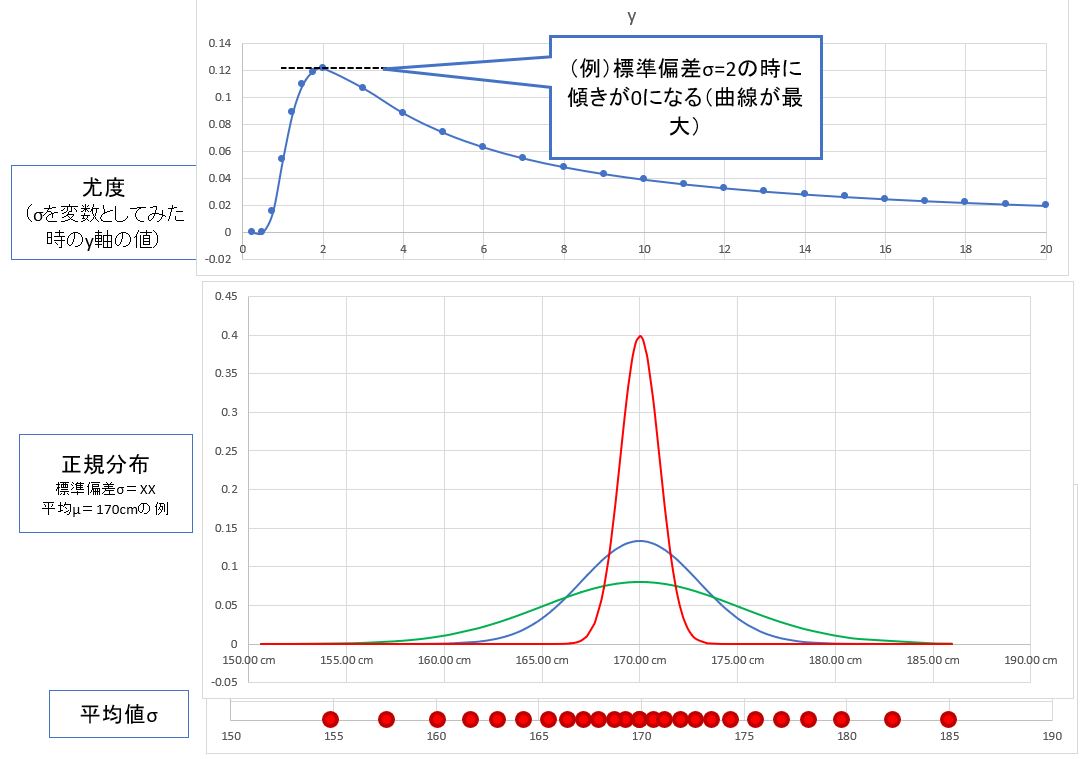
↓
・②結果として、「平均値μ(mean)」と「標準偏差σ(standard deviation)」の観点から、データ群に適合する正規分布を「最尤推定」する事に成功しました。
(図125)
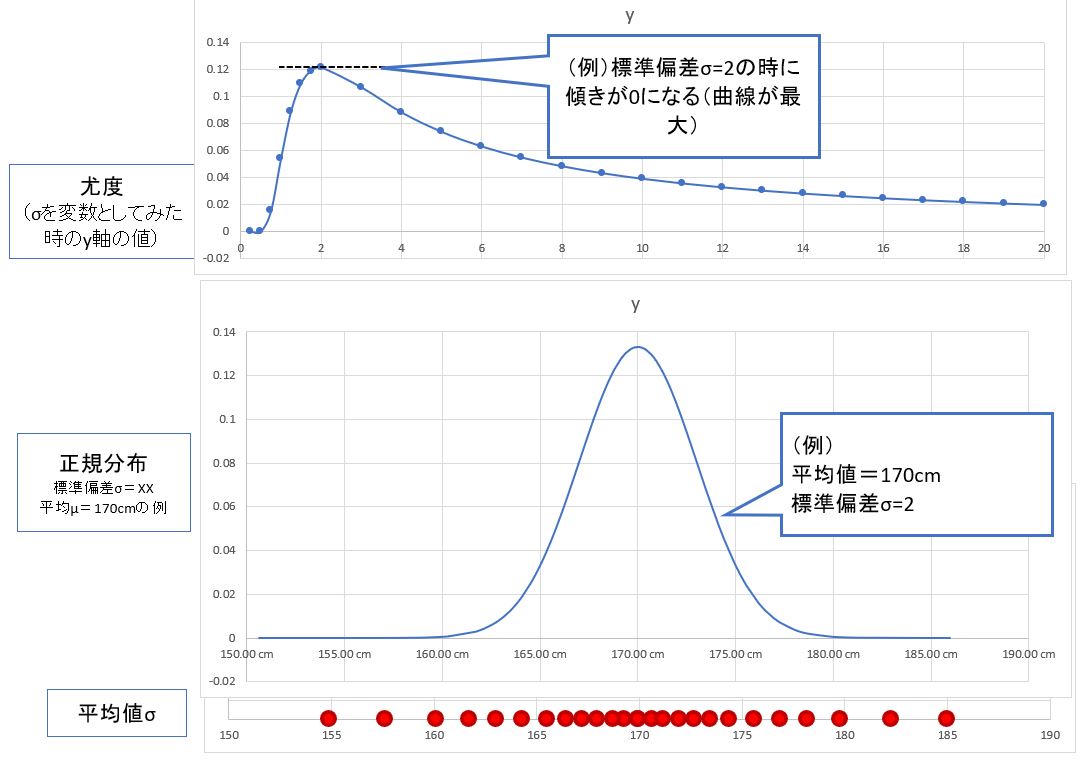
(備考)
これは数学的には、平均値μを定数、標準偏差σを変数として扱った時の曲線の傾き=0の点(つまり最大)です(=すなわち、σで「偏微分」した時に0になる地点)
●まとめ
確率:パラメータ ⇒ データの「確率」を算出
尤度:データ ⇒ パラメータの「尤もらしさ」を算出
最尤推定:尤度が最大となるパラメータ(データに対応する分布)を特定する
(1-3) 最尤推定の実際の計算方法は?