ニューラルネットワークでAND回路を学習させるJavaプログラムを作成したので、その解説を行います。
(0)目次&概説
(1) ニューラルネットワークの概要
(1-1) ニューラルネットワークとは?
(1-2) ニューラルネットワークの情報伝達の流れは?
(1-3) ディープラーニングとは?
(2) モデル化&計算方法
(2-1) モデル化
(2-2) 計算手法
(2-3) アウトプットイメージ
(3) プログラミング
(3-1) サンプルコード
(3-2) サンプルコード解説
(3-2-1) 解説1
(3-2-2) 解説2
(3-2-3) 解説3
(3-2-4) 解説4
(4) 結果と考察
(4-1) 答え合わせの方法
(4-2) グラフにより可視化
(1) ニューラルネットワークの概要
(1-1) ニューラルネットワークとは?
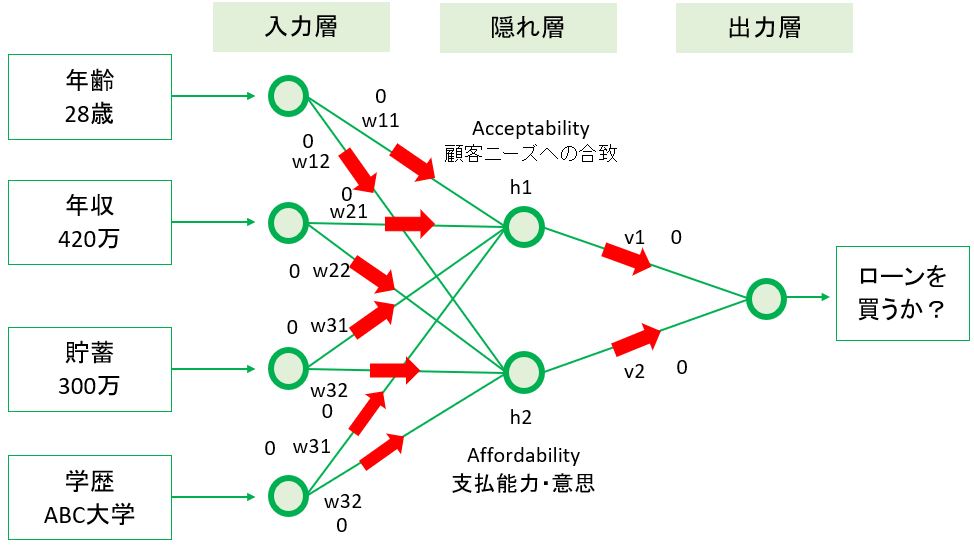
ニューラルネットワークとは、人工知能分野のアルゴリズムの一つで、「人間の脳」をモデルにしています。人間の脳もニューロンと呼ばれる神経細胞のネットワークから成っており、ニューロン同士で電気信号による情報の伝達が行われています。
(図1)
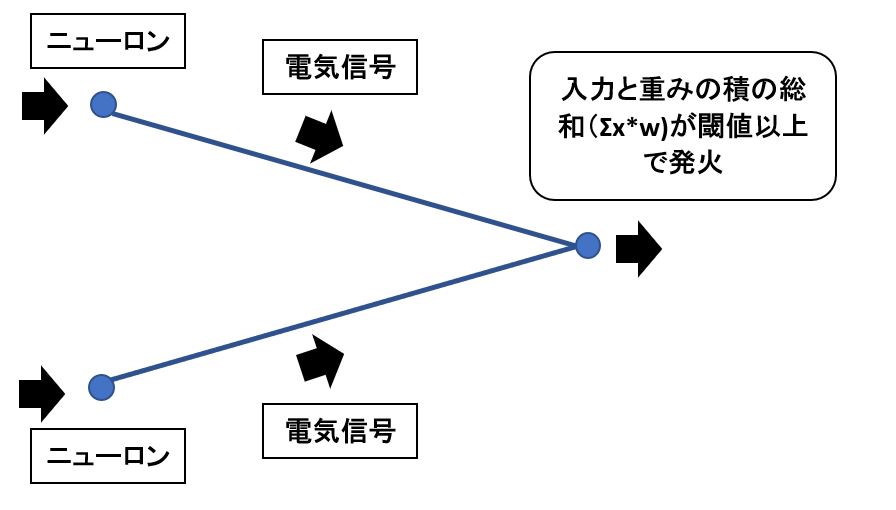
(1-2) ニューラルネットワークの情報伝達の流れは?
(図1)のようにニューロンは他のニューロンから入力信号(x)を受け取ると、それに重み(w)を乗じて次のニューロンに渡します。次のニューロンには複数のニューロンからの信号が届きますが、その合計がある閾値を超えた場合、発火してまた次のニューロンに信号を送ります。
(図2)
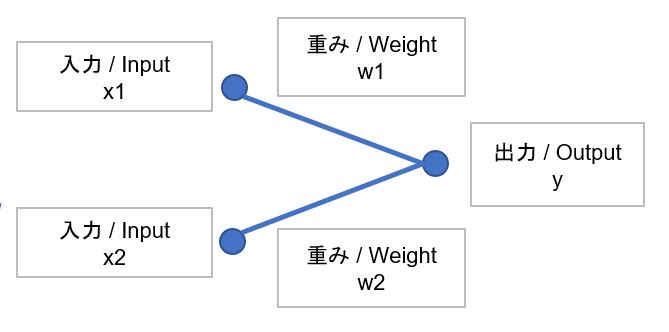
(1-3) ディープラーニングとは?
(図3)
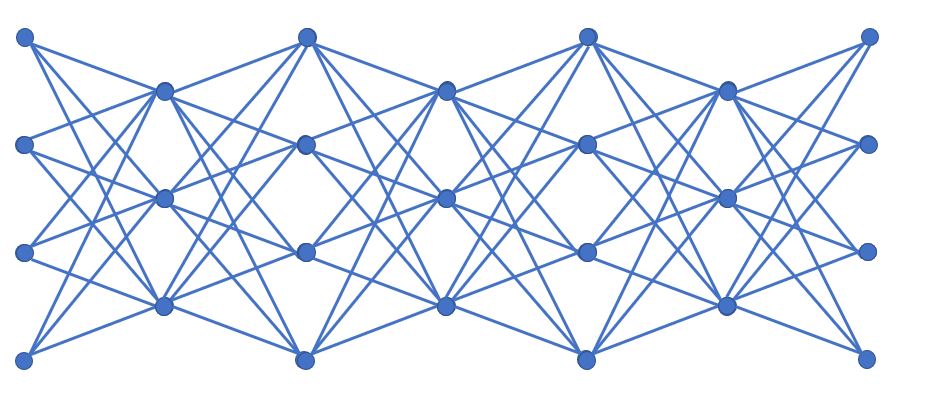
(2) モデル化&計算方法
ニューラルネットワークのモデルを用いて「AND回路」を学習させ、その学習の結果を用いて入力データが「発火するか?しないか?」を決定する境界線を算出するプログラムをJavaで実装します。まずは回路をモデル化し、各値の計算方法を確認していきます。
(2-1) モデル化
ニューラルネットワークの入力を\(x_{1}\)・\(x_{2}\)、重みを\(w_{1}\)・\(w_{2}\)、発火の閾値を\( \theta \)とすると、ニューロンの発火の式は次のように表現できます。
$$ w_{1}x_{1}+w_{2}x_{2}-\theta \geq 0\\\\
$$
また最終的に受け取る電気信号(出力)をyとすると次の2通りで表現されます。
$$ y = 1\ (w_{1}x_{1}+w_{2}x_{2}-\theta \geq 0)\\\\
y = 0\ (w_{1}x_{1}+w_{2}x_{2}-\theta < 0)\\\\
$$
★図を挿入
(2-2) 計算手法
(2-2-1) \(w_{1}\)、\(w_{2}\)、\(\theta\)の初期値を決定
まずは\(w_{1}\)、\(w_{2}\)、\(\theta\)の初期値を決定します。今回の例では次のように置きます。
$$w_{1}=0 、 w_{2}=0、 \theta=0$$
(2-2-2) \(y\)の値を計算
上記で決めた\(w_{1}\)、\(w_{2}\)、\( \theta \)の初期値を用いて\(y\)の値を計算します。
$$
y = 1\ (w_{1}x_{1}+w_{2}x_{2}-\theta \geq 0)\\\\
y = 0\ (w_{1}x_{1}+w_{2}x_{2}-\theta < 0)\\\\
$$
\(y\)の値を求める時に利用する\(x_{1}\)と\(x_{2}\)の値は次のように決定します。
(表1)
| count | x1 | x2 | t |
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 0 | 0 |
| 4 | 1 | 1 | 1 |
| 5 | 0 | 0 | 0 |
| 6 | 0 | 1 | 0 |
| 7 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 |
| ・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
ご覧の通り、AND回路の4つの入出力パターンを順番に繰り返しています。なので1回目の計算では\(x_{1}=0\)、\(x_{2}=0\)、\(t=0\)を使用します。count=4まで到達したら、また再び\(x_{1}=0\)、\(x_{2}=0\)、\(t=0\)に戻り、以降それをずっと繰り返していきます。
ちなみに\(t\)は「出力の正解値」と表現する文字で、ある入力\(x_{1}=0\)と\(x_{2}=0\)の組み合わせに対して計算した電気信号\(y\)と、その入力組合せにおける正解の出力\(t\)との差分を利用して修正量の計算し、次の学習に繋げて行く事で、正解\(t\)と計算結果\(y\)の乖離が段々と小さくなっていきます。
(2-2-3) \(\Delta w_{1}\)、\(\Delta w_{2}\)、\(\Delta\theta\)の値を計算
\(y\)の値が計算できたら、そこから\(\Delta w_{1}\)、\(\Delta w_{2}\)、\(\Delta\theta\)を次の式を用いて計算します。
$$
\Delta w_{1}=(t-y)x_{1}\\\\
\Delta w_{2}=(t-y)x_{2}\\\\
\Delta\theta=(y-t)\theta
$$
最後に、求めた\(\Delta w_{1}\)、\(\Delta w_{2}\)、\(\Delta\theta\)の値を用いて\(w_{1}\)、\(w_{2}\)、\(\theta\)の値を更新します。 $$ w_{1}^{n+1}=w_{1}^{n} +\Delta w_{1}\\\\
w_{2}^{n+1}=w_{2}^{n}+\Delta w_{2}\\\\
\theta^{n+1}=\theta^{n}+\Delta\theta
$$
ここで求めた\(w_{1}\)、\(w_{2}\)、\(\theta\)の値を次の値のインプットにして、再び最初の計算手順に戻り、次の\(y\)の値を計算します。\(x_{1}\)、\(x_{2}\)、\(t\)についてはAND回路の入出力の表に沿って、2回目の計算では\(x_{1}=0\)、\(x_{2}=1\)、\(t=0\)を使います。
イメージしやすいように、実際の計算結果は次のようになります。
(2-3) アウトプットイメージ
上記での各回の学習について学習結果の(\(w_{1}, w_{2}, \theta\))の値を次の式に代入し、\(x_{1}\)と\(x_{2}\)に関する直線の式として表現します。
$$ w_{1}x_{1}+w_{2}x_{2}-\theta = 0\\\\ $$ $$ x_{2} = \frac {-w_{1}x_{1}+\theta}{w_{2}}\\\\ $$
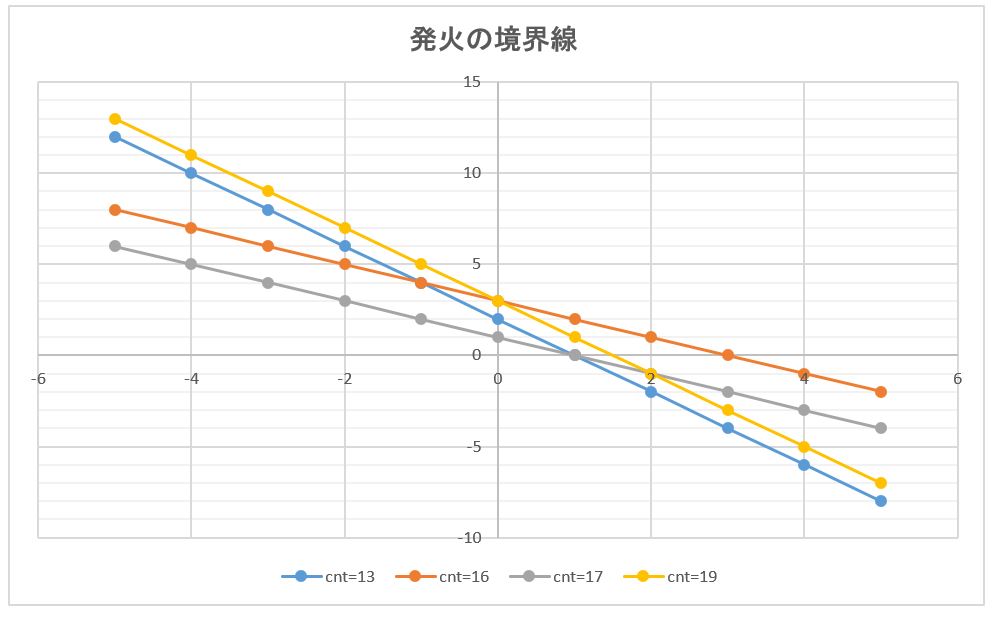
それをグラフとしてプロットしていき、最終的に収束する直線がAND回路が「発火するか?、しないか?」を分ける境界線になっている事を確認します。
>目次にもどる
(3) プログラミング
(3-1) サンプルコード
サンプルコードを紹介します。
/*******************************************/
/* ニューラルネットワークを用いたAND回路の学習
/* Coded by : Rainbow Engine
/*******************************************/
public class DeepLearn_AndGate {
public static void main(String args[]) {
//@@@ 解説1 @@@//
int N=4;
int x1[]=new int[N];
int x2[]=new int[N];
int t[]=new int[N];
x1[0]=0; x2[0]=0; t[0]=0;
x1[1]=0; x2[1]=1; t[1]=0;
x1[2]=1; x2[2]=0; t[2]=0;
x1[3]=1; x2[3]=1; t[3]=1;
int w1=0, w2=0, theta=0; //Set as default test Value
int y=0;
int dw1=0, dw2=0, dtheta=0;
int counter=0;
boolean flg[] = new boolean[4];
for(int i=0; i<N; i++) { flg[i]=false; }
//@@@ 解説2 @@@//
while(flg[0]==false || flg[1]==false || flg[2]==false || flg[3]==false) {
//@@@ 解説3 @@@//
for(int i=0; i<N; i++) { flg[i]=false; }
//@@@ 解説4 @@@//
for(int i=0; i<N; i++) {
//1.Update the variables
w1=w1+dw1; w2=w2+dw2; theta=theta+dtheta;
//2.Caluculate x1*w1+x2*w2-theta & decide y
if( (x1[i]*w1+x2[i]*w2-theta)>=0 ) {y=1;}
else{y=0;}
//3.Calculate dw1,dw2,dtheta
dw1=(t[i]-y)*x1[i]; dw2=(t[i]-y)*x2[i]; dtheta=(y-t[i]);
//4.Check the result
if(dw1==0 && dw2==0 && dtheta==0) {
flg[i]=true;
}
//@@@ 解説5 @@@//
System.out.println("No: "+(counter+1)+" x1=["+x1[i]+"] x2=["+x2[i]+"] t=["+t[i]+"] w1=["+w1+"] w2=["+w2+"] theta=["+theta+"] y=["+y+"] t-y=["+(t[i]-y)+"] dw1=["+dw1+"] dw2=["+dw2+"] dtheta=["+dtheta+"] tr1=["+flg[0]+"] tr2=["+flg[1]+"] tr3=["+flg[2]+"] tr4=["+flg[3]+"]");
counter++;
}
}
System.out.println("Result : "+w1+"*(x1)+"+w2+"*(x2)-"+theta+"=0");
}
}
<実行結果のサンプル>
No: 1 x1=[0] x2=[0] t=[0] w1=[0] w2=[0] theta=[0] y=[1] t-y=[-1] dw1=[0] dw2=[0] dtheta=[1] tr1=[false] tr2=[false] tr3=[false] tr4=[false] No: 2 x1=[0] x2=[1] t=[0] w1=[0] w2=[0] theta=[1] y=[0] t-y=[0] dw1=[0] dw2=[0] dtheta=[0] tr1=[false] tr2=[true] tr3=[false] tr4=[false] No: 3 x1=[1] x2=[0] t=[0] w1=[0] w2=[0] theta=[1] y=[0] t-y=[0] dw1=[0] dw2=[0] dtheta=[0] tr1=[false] tr2=[true] tr3=[true] tr4=[false] No: 4 x1=[1] x2=[1] t=[1] w1=[0] w2=[0] theta=[1] y=[0] t-y=[1] dw1=[1] dw2=[1] dtheta=[-1] tr1=[false] tr2=[true] tr3=[true] tr4=[false] No: 5 x1=[0] x2=[0] t=[0] w1=[1] w2=[1] theta=[0] y=[1] t-y=[-1] dw1=[0] dw2=[0] dtheta=[1] tr1=[false] tr2=[false] tr3=[false] tr4=[false] No: 6 x1=[0] x2=[1] t=[0] w1=[1] w2=[1] theta=[1] y=[1] t-y=[-1] dw1=[0] dw2=[-1] dtheta=[1] tr1=[false] tr2=[false] tr3=[false] tr4=[false] No: 7 x1=[1] x2=[0] t=[0] w1=[1] w2=[0] theta=[2] y=[0] t-y=[0] dw1=[0] dw2=[0] dtheta=[0] tr1=[false] tr2=[false] tr3=[true] tr4=[false] No: 8 x1=[1] x2=[1] t=[1] w1=[1] w2=[0] theta=[2] y=[0] t-y=[1] dw1=[1] dw2=[1] dtheta=[-1] tr1=[false] tr2=[false] tr3=[true] tr4=[false] No: 9 x1=[0] x2=[0] t=[0] w1=[2] w2=[1] theta=[1] y=[0] t-y=[0] dw1=[0] dw2=[0] dtheta=[0] tr1=[true] tr2=[false] tr3=[false] tr4=[false] No: 10 x1=[0] x2=[1] t=[0] w1=[2] w2=[1] theta=[1] y=[1] t-y=[-1] dw1=[0] dw2=[-1] dtheta=[1] tr1=[true] tr2=[false] tr3=[false] tr4=[false] No: 11 x1=[1] x2=[0] t=[0] w1=[2] w2=[0] theta=[2] y=[1] t-y=[-1] dw1=[-1] dw2=[0] dtheta=[1] tr1=[true] tr2=[false] tr3=[false] tr4=[false] No: 12 x1=[1] x2=[1] t=[1] w1=[1] w2=[0] theta=[3] y=[0] t-y=[1] dw1=[1] dw2=[1] dtheta=[-1] tr1=[true] tr2=[false] tr3=[false] tr4=[false] No: 13 x1=[0] x2=[0] t=[0] w1=[2] w2=[1] theta=[2] y=[0] t-y=[0] dw1=[0] dw2=[0] dtheta=[0] tr1=[true] tr2=[false] tr3=[false] tr4=[false] No: 14 x1=[0] x2=[1] t=[0] w1=[2] w2=[1] theta=[2] y=[0] t-y=[0] dw1=[0] dw2=[0] dtheta=[0] tr1=[true] tr2=[true] tr3=[false] tr4=[false] No: 15 x1=[1] x2=[0] t=[0] w1=[2] w2=[1] theta=[2] y=[1] t-y=[-1] dw1=[-1] dw2=[0] dtheta=[1] tr1=[true] tr2=[true] tr3=[false] tr4=[false] No: 16 x1=[1] x2=[1] t=[1] w1=[1] w2=[1] theta=[3] y=[0] t-y=[1] dw1=[1] dw2=[1] dtheta=[-1] tr1=[true] tr2=[true] tr3=[false] tr4=[false] No: 17 x1=[0] x2=[0] t=[0] w1=[2] w2=[2] theta=[2] y=[0] t-y=[0] dw1=[0] dw2=[0] dtheta=[0] tr1=[true] tr2=[false] tr3=[false] tr4=[false] No: 18 x1=[0] x2=[1] t=[0] w1=[2] w2=[2] theta=[2] y=[1] t-y=[-1] dw1=[0] dw2=[-1] dtheta=[1] tr1=[true] tr2=[false] tr3=[false] tr4=[false] No: 19 x1=[1] x2=[0] t=[0] w1=[2] w2=[1] theta=[3] y=[0] t-y=[0] dw1=[0] dw2=[0] dtheta=[0] tr1=[true] tr2=[false] tr3=[true] tr4=[false] No: 20 x1=[1] x2=[1] t=[1] w1=[2] w2=[1] theta=[3] y=[1] t-y=[0] dw1=[0] dw2=[0] dtheta=[0] tr1=[true] tr2=[false] tr3=[true] tr4=[true] No: 21 x1=[0] x2=[0] t=[0] w1=[2] w2=[1] theta=[3] y=[0] t-y=[0] dw1=[0] dw2=[0] dtheta=[0] tr1=[true] tr2=[false] tr3=[false] tr4=[false] No: 22 x1=[0] x2=[1] t=[0] w1=[2] w2=[1] theta=[3] y=[0] t-y=[0] dw1=[0] dw2=[0] dtheta=[0] tr1=[true] tr2=[true] tr3=[false] tr4=[false] No: 23 x1=[1] x2=[0] t=[0] w1=[2] w2=[1] theta=[3] y=[0] t-y=[0] dw1=[0] dw2=[0] dtheta=[0] tr1=[true] tr2=[true] tr3=[true] tr4=[false] No: 24 x1=[1] x2=[1] t=[1] w1=[2] w2=[1] theta=[3] y=[1] t-y=[0] dw1=[0] dw2=[0] dtheta=[0] tr1=[true] tr2=[true] tr3=[true] tr4=[true] Result : 2*(x1)+1*(x2)-3=0
(3-2) サンプルコード解説
(3-2-1) 解説1
サンプルPGの「//@@@ 解説1 @@@//」では変数の定義を行っています。
//@@@ 解説1 @@@//
int N=4;
int x1[]=new int[N];
int x2[]=new int[N];
int t[]=new int[N];
x1[0]=0; x2[0]=0; t[0]=0;
x1[1]=0; x2[1]=1; t[1]=0;
x1[2]=1; x2[2]=0; t[2]=0;
x1[3]=1; x2[3]=1; t[3]=1;
int w1=0, w2=0, theta=0; //Set as default test Value
int y=0;
int dw1=0, dw2=0, dtheta=0;
int counter=0;
boolean flg[] = new boolean[4];
for(int i=0; i<N; i++) { flg[i]=false; }
| 変数名 | 説明 |
| N | テストデータの個数(AND回路の入力が4通りのため) |
| x1[N], x2[N] | 入力ニューロン#1,#2の電気信号。 テストデータの個数(N=4)だけ入力のパターンを用意します。 |
| t[N] | 出力yの正解値。 こちらも入力と同様、テストデータの個数(N=4)だけ入力のパターンを用意します。 |
| w1,w2 | 入力ニューロン#1,#2の重み |
| theta | ニューロンが発火する閾値θ(ニューロンは発火すると、また次のニューロンへ情報を伝達する) |
| y | 出力(入力ニューロンから得られる電気信号) |
| dw1,dw2 | 誤り訂正法による「w1」、「w2」の修正量(Δw1、Δw2) |
| dtheta | 誤り訂正法による「theta」の修正量(Δθ) |
| flag[N] | 完了条件を判定するためのフラグです。N=4パターンあり、それぞれがAND回路の4つの入力タイプに対応しています([0,0]、[0,1]、[1,0]、[1,1])。 |
(3-2-2) 解説2
サンプルPGの「//@@@ 解説2 @@@//」ではループの終了条件の定義を行っており「AND回路の4パターンの入力データ([0,0]、[0,1]、 [1,0]、[1,1])の全てに対して、修正量(dw1,dw2,dθ)が0になる事」です。
今回は4パターンの入力それぞれに対してboolean型のフラグを割り当てて「4つの条件のうち、どれか一つでも修正量が0でない(false)」ならば、ループを続行するという条件にしています。
| 変数名 | AND回路の入力 | AND回路の期待する出力(t) |
| flag1 | [0,0] | [0] |
| flag2 | [0,1] | [0] |
| flag3 | [1,0] | [0] |
| flag4 | [1,1] | [1] |
//@@@ 解説2 @@@//
while(flg[0]==false || flg[1]==false || flg[2]==false || flg[3]==false) {
(3-2-3) 解説3
サンプルPGの「//@@@ 解説3 @@@//」ではループの開始時に一旦、4つのフラグを全てfalse(修正量が0でない)にします。この後にforループで4パターンのそれぞれの入力を順番に見ていき、修正量(dw1,dw2,dθ)が全て0なら、該当の入力のフラグをtrue(修正量0)に更新します。
//@@@ 解説3 @@@//
for(int i=0; i<N; i++) { flg[i]=false; }
(3-2-4) 解説4
4パターンの入力データ([0,0]、[0,1]、 [1,0]、[1,1])をforループで回し、それぞれについて誤り修正法を適用していきます。ループの中は次の4つの処理から成り立っています。
1. Update the variables
x1, x2, tを初期化し、重みw1,w2と閾値thetaを計算する
$$
w_{1}^{n+1}=w_{1}^{n} +\Delta w_{1}\\\\
w_{2}^{n+1}=w_{2}^{n}+\Delta w_{2}\\\\
\theta^{n+1}=\theta^{n}+\Delta\theta
$$
2. Caluculate x1*w1+x2*w2-theta & decide y
計算した各値を元に(x1*w1+x2*w2-theta)を算出し、0より大きいか否かでyを決定する。
$$
w_{1}x_{1}+w_{2}x_{2}-\theta
$$
3. Calculate dw1,dw2,dtheta
dw1,dw2,dθの値を計算しています。
$$
\Delta w_{1}=(t-y)x_{1}\\\\
\Delta w_{2}=(t-y)x_{2}\\\\
\Delta\theta=(y-t)\theta
$$
4. Check the result
dw1,dw2,dθが0かどうかチェックし、フラグの更新処理をしています。
//@@@ 解説4 @@@//
for(int i=0; i<N; i++) {
//1.Update the variables
w1=w1+dw1; w2=w2+dw2; theta=theta+dtheta;
//2.Caluculate x1*w1+x2*w2-theta & decide y
if( (x1[i]*w1+x2[i]*w2-theta)>=0 ) {y=1;}
else{y=0;}
//3.Calculate dw1,dw2,dtheta
dw1=(t[i]-y)*x1[i]; dw2=(t[i]-y)*x2[i]; dtheta=(y-t[i]);
//4.Check the result
if(dw1==0 && dw2==0 && dtheta==0) {
flg[i]=true;
}
ちなみに「③dw1,dw2,dθの値を計算」について、Δで増加させるか?減少させるか?はおおよそ以下の方針で判断をしています。
例えばt=1でy=0の場合など「入力が小さ過ぎる」or「閾値が大き過ぎる」事が原因のため、「wを大きくする」or「θを小さくする」よう、下記のように修正する。
(3-2-5) 解説5
次に示す行はデバッグのための出力であり、処理ロジックとは関係ありません。
//@@@ 解説5 @@@//
System.out.println("No: "+(counter+1)+" x1=["+x1[i]+"] x2=["+x2[i]+"] t=["+t[i]+"] w1=["+w1+"] w2=["+w2+"] theta=["+theta+"] y=["+y+"] t-y=["+(t[i]-y)+"] dw1=["+dw1+"] dw2=["+dw2+"] dtheta=["+dtheta+"] tr1=["+flg[0]+"] tr2=["+flg[1]+"] tr3=["+flg[2]+"] tr4=["+flg[3]+"]");
counter++;
(4) 結果と考察
(4-1) 答え合わせの方法
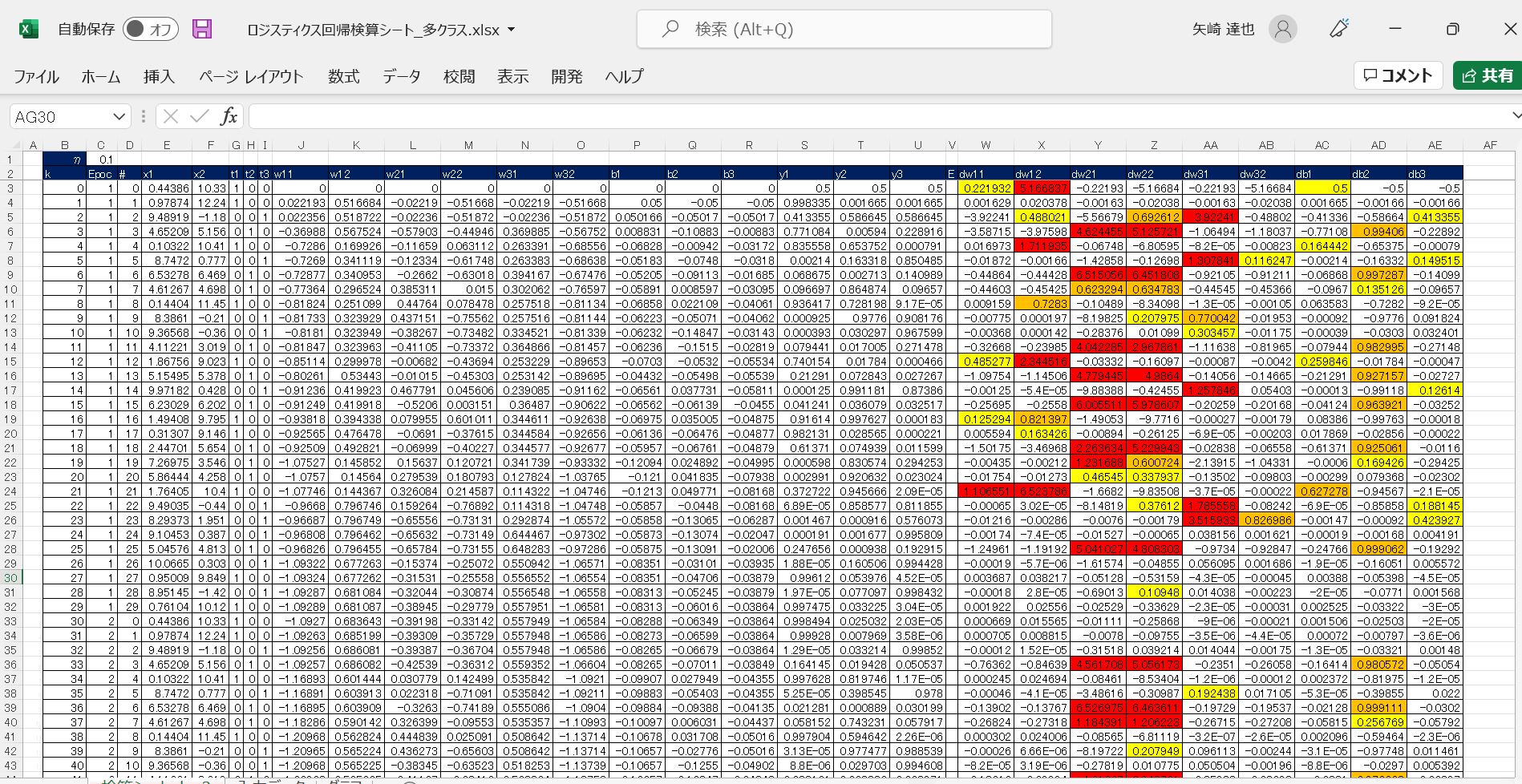
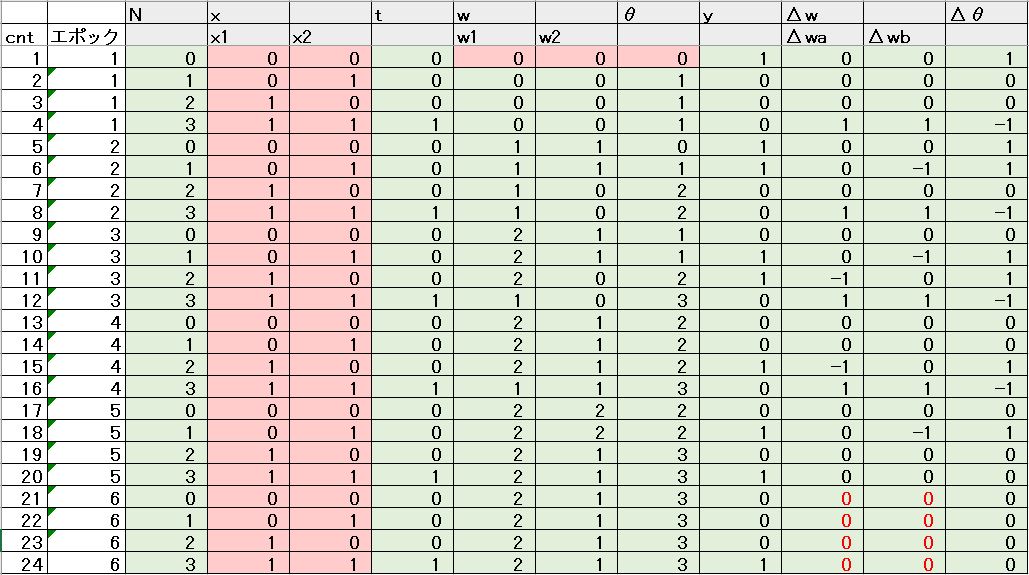
答え合わせをするために、事前にエクセルでも同じ計算を実施しており、プログラムの結果とエクセルの結果を比較しています。
| N | x | t | w | θ | y | Δw | Δθ | |||||
| cnt | エポック | x1 | x2 | w1 | w2 | Δwa | Δwb | |||||
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 2 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 3 | 1 | 2 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 4 | 1 | 3 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | -1 |
| 5 | 2 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 6 | 2 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | -1 | 1 |
| 7 | 2 | 2 | 1 | 0 | 0 | 1 | 0 | 2 | 0 | 0 | 0 | 0 |
| 8 | 2 | 3 | 1 | 1 | 1 | 1 | 0 | 2 | 0 | 1 | 1 | -1 |
| 9 | 3 | 0 | 0 | 0 | 0 | 2 | 1 | 1 | 0 | 0 | 0 | 0 |
| 10 | 3 | 1 | 0 | 1 | 0 | 2 | 1 | 1 | 1 | 0 | -1 | 1 |
| 11 | 3 | 2 | 1 | 0 | 0 | 2 | 0 | 2 | 1 | -1 | 0 | 1 |
| 12 | 3 | 3 | 1 | 1 | 1 | 1 | 0 | 3 | 0 | 1 | 1 | -1 |
| 13 | 4 | 0 | 0 | 0 | 0 | 2 | 1 | 2 | 0 | 0 | 0 | 0 |
| 14 | 4 | 1 | 0 | 1 | 0 | 2 | 1 | 2 | 0 | 0 | 0 | 0 |
| 15 | 4 | 2 | 1 | 0 | 0 | 2 | 1 | 2 | 1 | -1 | 0 | 1 |
| 16 | 4 | 3 | 1 | 1 | 1 | 1 | 1 | 3 | 0 | 1 | 1 | -1 |
| 17 | 5 | 0 | 0 | 0 | 0 | 2 | 2 | 2 | 0 | 0 | 0 | 0 |
| 18 | 5 | 1 | 0 | 1 | 0 | 2 | 2 | 2 | 1 | 0 | -1 | 1 |
| 19 | 5 | 2 | 1 | 0 | 0 | 2 | 1 | 3 | 0 | 0 | 0 | 0 |
| 20 | 5 | 3 | 1 | 1 | 1 | 2 | 1 | 3 | 1 | 0 | 0 | 0 |
| 21 | 6 | 0 | 0 | 0 | 0 | 2 | 1 | 3 | 0 | 0 | 0 | 0 |
| 22 | 6 | 1 | 0 | 1 | 0 | 2 | 1 | 3 | 0 | 0 | 0 | 0 |
| 23 | 6 | 2 | 1 | 0 | 0 | 2 | 1 | 3 | 0 | 0 | 0 | 0 |
| 24 | 6 | 3 | 1 | 1 | 1 | 2 | 1 | 3 | 1 | 0 | 0 | 0 |

(4-2) グラフにより可視化
また、各繰り返し時点でのw1, w2, θの結果を踏まえて数式のグラフを書いていく事で、繰り返していく毎に収束に向かっていく様子を見る事が出来ます。