(1) Newton法で平方根を求めるJavaのサンプルプログラム
(1-1) Newton法の式を簡単に復習
(1-2) Newton法のサンプルプログラム
(1) Newton法で平方根を求めるJavaのサンプルプログラム
一変数の非線形方程式の近似解を反復的に求めるアルゴリズムである「ニュートン法」のプログラムをJavaで実装した例を紹介します。
【おまけ】
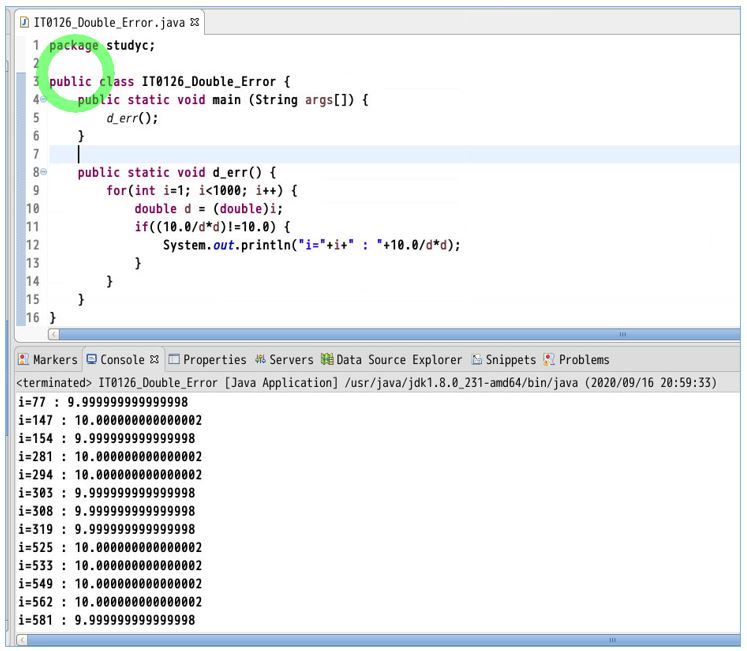
特に今回はdouble型の誤差(double型で発生する誤差について)を解消し、より高精度に解を求めるために、doubleに代わりBigDecimalを使って実装しています。
(1-1) Newton方の式を簡単に復習
①一般的な直線の式
点\((x_{1}, y_{1})\)を通って傾きが \(a\) の直線の式は
$$
y-y_{1}=a(x-x_{1})
$$
②反復1回目の接線
方程式\(y=f(x)\)でニュートン法の初期値を\(x_{1}\)とすると、1回目の接線は点「\((x_{1},f(x_{1})\)」を通って傾きが\(f'(x_{1})\)の直線になります。 これらを①の式に代入すると
$$
y-f(x_{1})=f'(x_{1})(x-x_{1})
$$
③反復1回目の解(【★実装に使う式】)
上記の式で\(y=0\)を代入して\(x\)について解くと、反復1回目の解(\(x_{2}\)とする)が求まります
この反復1回目の解\(x\)を\(x_{2}\)と呼ぶとすると
$$
x_{2}=x_{1}-\frac {f(x_{1})}{f'(x_{1})}
$$
となり、同様に反復2回目の解を求める式は次の通りです。
$$
x_{3}=x_{2}-\frac {f(x_{2})}{f'(x_{2})}
$$
この計算を繰り返していく事で\(x\)がどんどん解に近づいていきます。
>目次にもどる
(1-2) Newton法のサンプルプログラム
今回のプログラムは上記ニュートン法の式(【★実装に使う式】)に\(f(x)=x^2-a\)を適用した式で実装しています。
$$
x_{n}=x_{n-1}-\frac {(x_{n-1}^2-a)}{2x_{n-1}}
$$
x = x.subtract(x.multiply(x).subtract(a).divide(c2.multiply(x),51,RoundingMode.HALF_UP)); delta = x.multiply(x).subtract(a).abs();
(サンプルPG)
⇒BigDecimalの使い方を確認したい方は、こちらの記事「JavaのBigDecimalの使い方」をご参照ください。
import java.math.BigDecimal;
import java.math.RoundingMode;
public class Newton1 {
public static void main(String[] args) {
//平方根を求める数字「a」を引数から取得
BigDecimal a = new BigDecimal(args[0]);
//引数から「x」の初期値を取得(一旦は「a」と同じ値にしています)
BigDecimal x = new BigDecimal(args[0]);
//「f(x)=x*x-a」を微分した結果「f'(x)=2x」の係数「2」をBigDecimalで定義
BigDecimal c2 = new BigDecimal("2");
//誤差の閾値をBigDecimalで定義
BigDecimal err = BigDecimal.valueOf(1E-50);
//誤差の初期値をBigDecimalで定義
BigDecimal delta = new BigDecimal("1");
int count = 0;
while (err.compareTo(delta)<0 ) {
//【★実装に使う式】に、今回の方程式「f(x)=x*x-a」を当てはめて計算した式
x = x.subtract(x.multiply(x).subtract(a).divide(c2.multiply(x),51,RoundingMode.HALF_UP));
//誤差の計算
// ⇒今回はaの平方根を求めているのでxを二乗したらaに限りなく近くなるはず
// ⇒よってx*x-aの絶対値を計算する
delta = x.multiply(x).subtract(a).abs();
++count;
System.out.println("Count="+count+" Error="+delta);
}
System.out.println("x = " + x);
System.out.println("x * x = " + x.multiply(x));
}
}
(実行時の注意点)
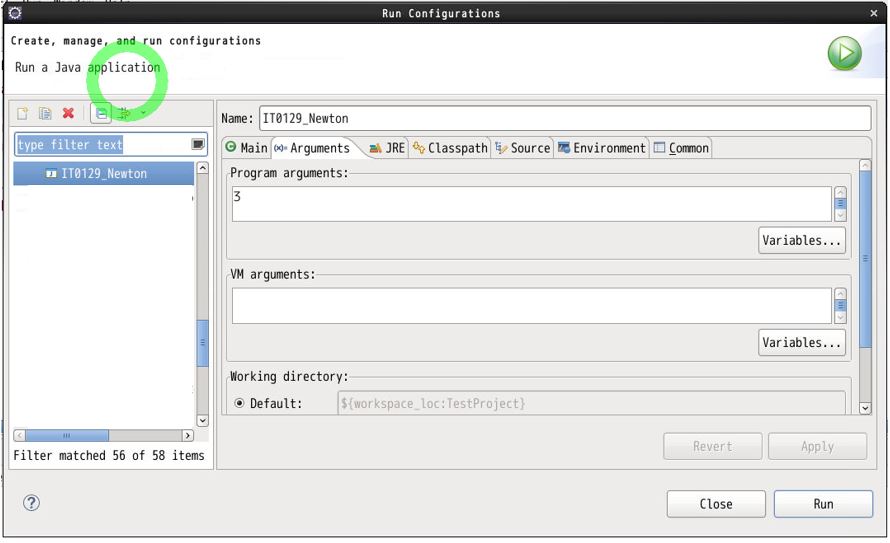
Eclipseで実行する場合は「Run Configurations」から実行時の引数を指定します。
(図121)
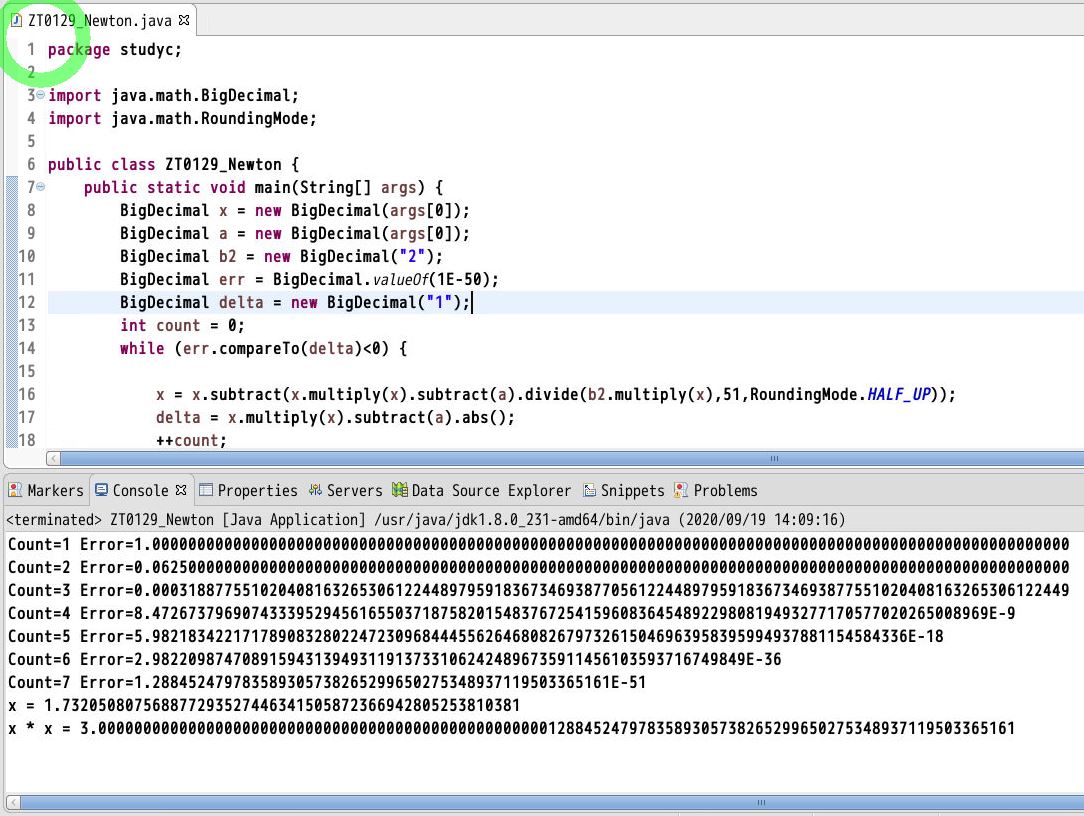
(実行結果例)
引数に「3」を与えて実行した例です(ルート3なので1.73205・・・を求める計算になります)。
(図122)
(操作動画)引数の操作からプログラム実行の簡単な動画です。