木構造の探索における計算量の違いや木構造の種類について(B木／二分木／2-3探索木)

(１) 木構造の探索における計算量の違いや木構造の種類について(B木／二分木／2-3探索木)
　(１-１) 木構造について
　(１-２) 「B木」構造
　(１-３) 「二分木」構造
　(１-４) 「2-3探索木」構造
　(１-５) 比較表①：計算量のオーダー
　(１-６) 比較表②：平衡の保ち方

(１) 木構造の探索における計算量の違いや木構造の種類について(B木／二分木／2-3探索木)

今回は「「B木」、「二分木」、「2-3探索木」の３つの木構造について、探索の計算量や特徴などを纏めます。

(１-１) 木構造について

木構造とはデータを探索するアルゴリズムを使用する際に、探索元のデータを格納するデータ構造の事です。見た目が「木」のように枝分岐しているため「木構造」と呼ばれています。
木はノード（点）とエッジ（線）から成り、次の条件を満たす必要があります。 ①ノードが環状になっていない事（輪になっていない）②全てのノードが連結されている（全てのノードが辿れる）③エッジは向きを持っていない

（図１１１）

＞目次にもどる

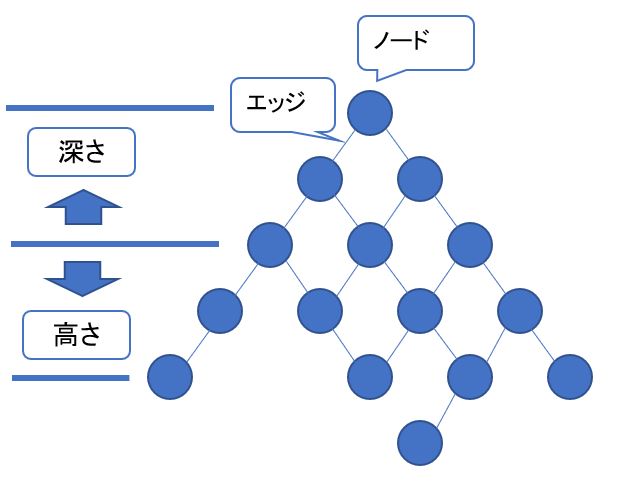
(１-２) 「B木」構造

■子ノードの規則
・全ての子ノードが同じ階層にいる必要があります。
・子ノードはM個持ち得ます（M≧3）
■使用シーン
データが「ストレージ」に格納されている状況で利用します。ツリーの高さを減らし、枝を増やす事で高速な探索を実現します。
■使用例
多くのデータベースのDBMSのインデックス構造として利用されています（OracleDB他）。

＞目次にもどる

(１-３) 「二分木」構造

■子ノードの規則
・0～2個の子ノートを持ちます（3つ以上は不可）
■使用シーン
データが「メモリ上」でソートされている条件下で利用します。主にアプリ開発の実装（プログラミング）で利用されます。

＞目次にもどる

(１-４) 3探索木」構造

■子ノードの規則
・最大3つの子ノードを持つ
・値が1つのノード　⇒　子は2つ
・値が2つのノード　⇒　子は3つ

＞目次にもどる

(１-５) 比較表①：計算量のオーダー

（表）

アルゴリズム	子ノード数	探索	データ追加・削除
二分探索	– （木ではない）	logN	× （データ増減がある場合は実用的でない）
2-3探索木	2～3	logN	logN （赤黒木・AVL木）
B木	M (M≧3)	logN	logN
平衡二分木	2	logN	logN （赤黒木・AVL木）

＞目次にもどる

(１-６) 比較表②：平衡の保ち方

木構造には「バランス」の概念があり、探索を効率良く行うためには木の「平衡を保つ」必要があります。

「平衡」の条件は具体的には「全てのリーフノード(葉)の深さがおおよそ同じに保たれている事」になります。次の表では木構造の種類毎にどのように平衡を保つのか？の概要を記載しています。

（表）

アルゴリズム	平衡の保ち方
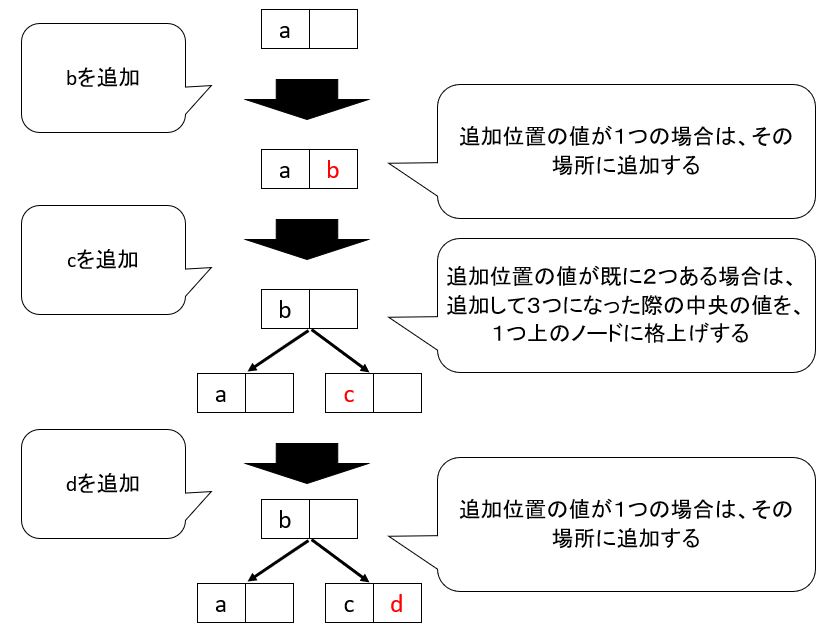
2-3探索木	■Insertの流れ　→★（図１６１） ①挿入ポイントを探索します（最下層に挿入する） ②追加位置の値が１つの場合は、その場所に追加する ③追加位置の値が既に２つある場合は、追加して３つになった際の中央の値を、１つ上のノードに格上げする （※最悪のケース、根まで繰り返し伝播する）
B木	■Insertの流れ　→★（図１６１） 「2-3探索木」と同じ手順
平衡二分木	平衡木にもいくつか種類がありますが、次に紹介する平衡木は平衡を保つ仕組みを持っています。 ①AVL木 ②赤黒木

（図１６１）

（備考①）二分木について
・探索回数は二分を繰り返すためlogNであるが、これは完全二分木の時の話です（葉付近以外のノードで全て２つの子を持つ）
・二分木で平衡でない木（例：○―○―○―○の様な一直線）の場合は逐次探索と差が無くなってしまいます。
・そのため、表中で記載している「AVL木」や「赤黒木」といった平衡を保つ仕組みが必要となります。

＞目次にもどる