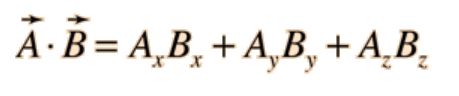<目次>
(1) Pythonで行列の計算方法をご紹介(Numpyを使用した四則演算や内積計算)
(1-1) 概要
(1-2) STEP1:Numpyのインストール
(1-3) STEP2:行列の定義
(1-4) STEP3:行列の演算
(1-5) 補足:ベクトルの場合
(1-6) 内積とは?
(1) Pythonで行列の計算方法をご紹介(Numpyを使用した四則演算や内積計算)
(1-1) 概要
I = [[1,0],[0,1]] A = [[1,2],[3,4]]
[[1, 0], [0, 1], [1, 2], [3, 4]]
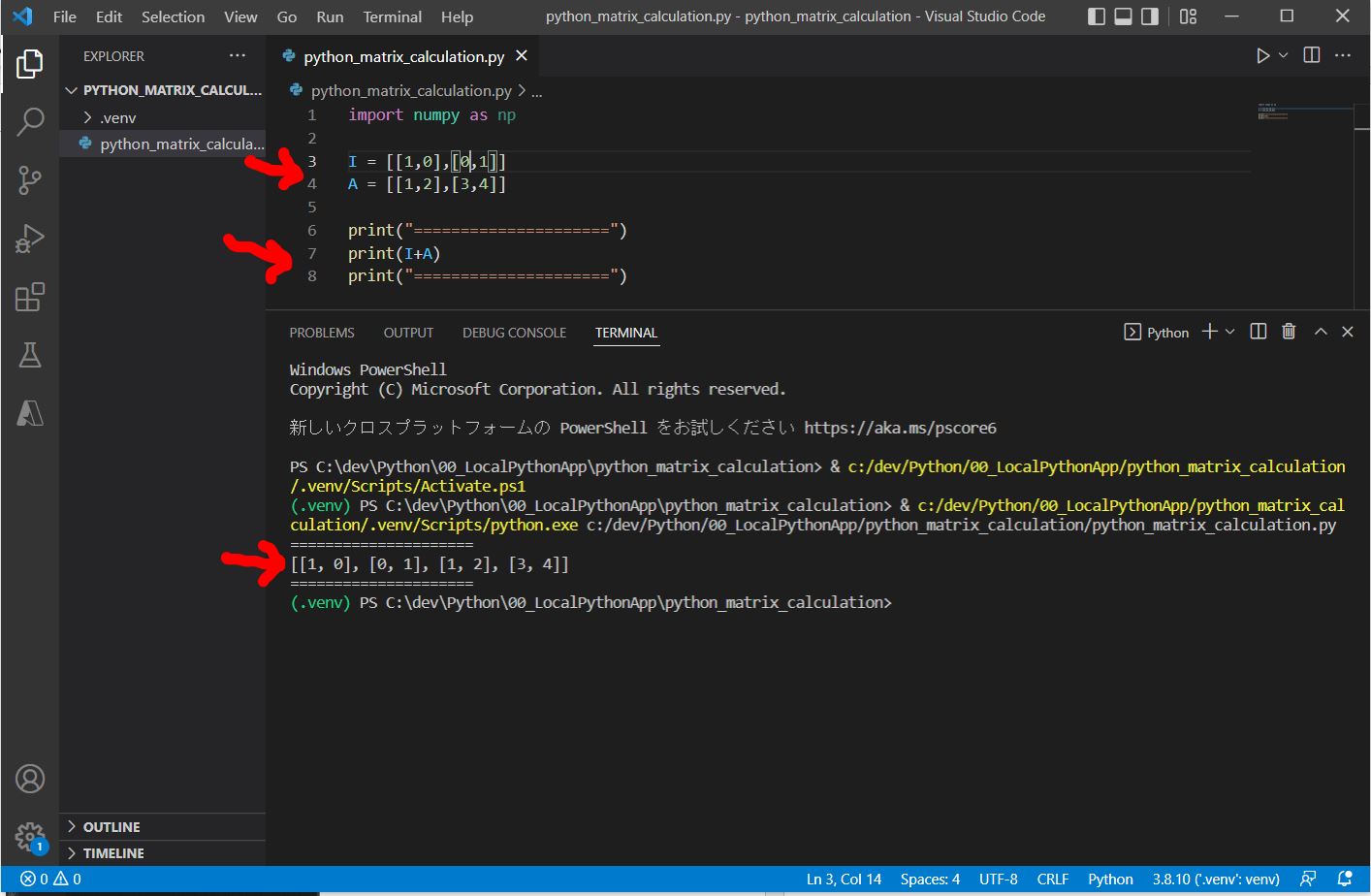
これを防ぎ、正しく行列の計算を行う方法はいくつかありますが、今回はNumpyを用いた方法をご紹介します。Numpyライブラリは数値計算や科学技術計算で非常に良く使われているライブラリで、線形代数の演算なども効率良く行う事ができるのでオススメです。
| No | 評価 | 概要 |
| 方法① | △ | forループで各要素を足し合わせていく |
| 方法② | ○ | 行列の和を計算する関数(例:add_matrix())を予め準備して、add_matrix(I,A)のように利用する |
| 方法③ | ◎ | Numpyライブラリを使用する |
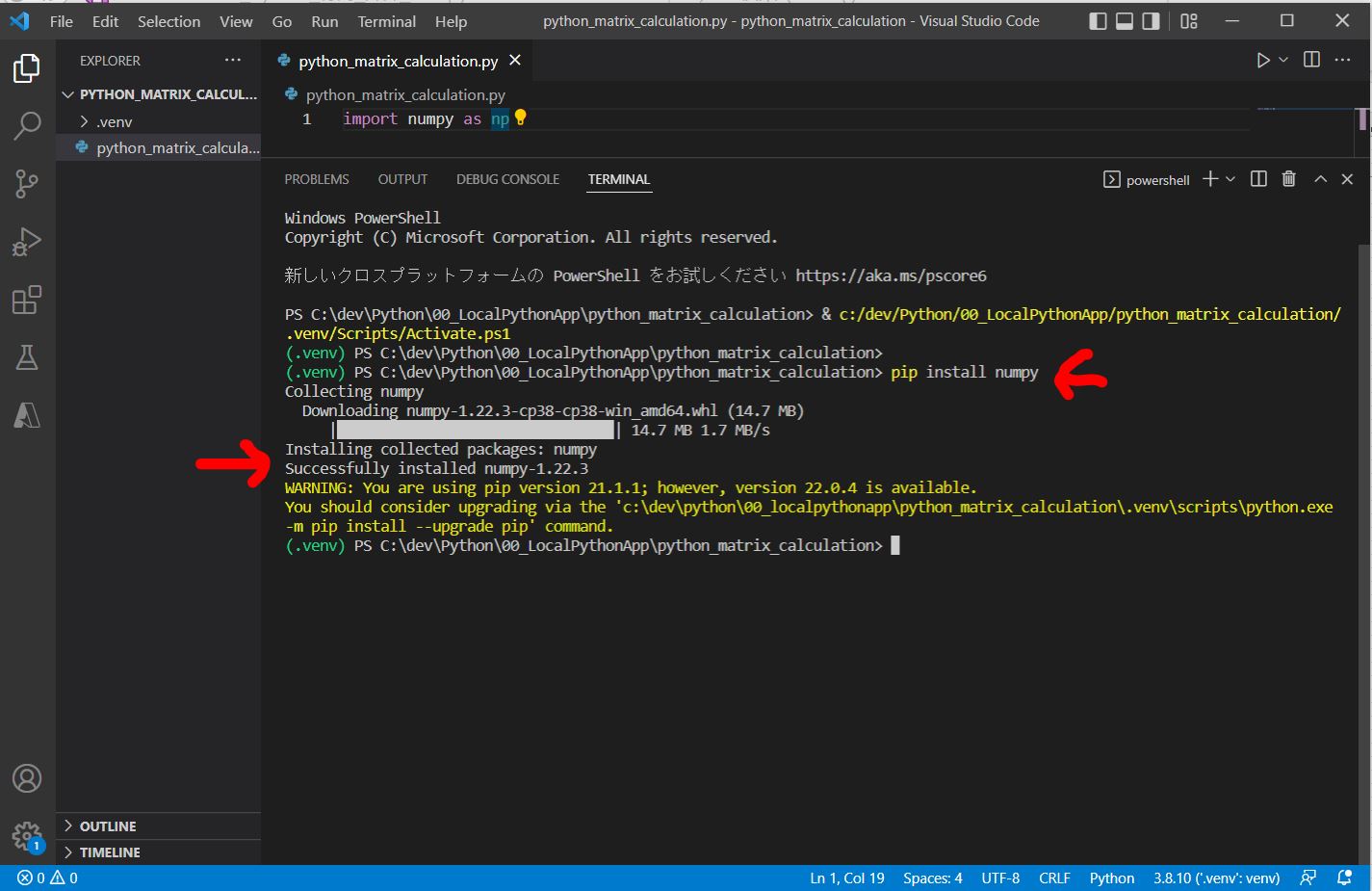
(1-2) STEP1:Numpyのインストール
> pip install numpy
Collecting numpy
Downloading numpy-1.22.3-cp38-cp38-win_amd64.whl (14.7 MB)
|████████████████████████████████| 14.7 MB 1.7 MB/s
Installing collected packages: numpy
Successfully installed numpy-1.22.3
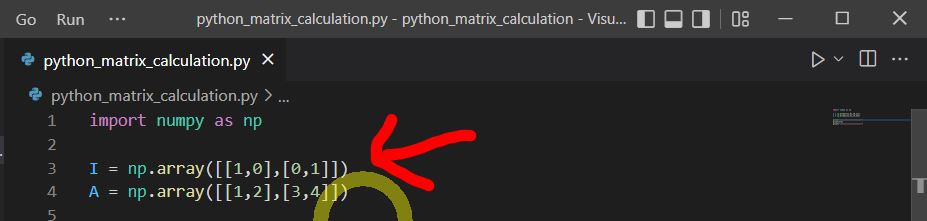
(1-3) STEP2:行列の定義
I = np.array([[1,0],[0,1]]) A = np.array([[1,2],[3,4]])
(1-4) STEP3:行列の演算
あとは、通常の変数の演算と同じような形で四則演算や、行列の演算(内積など)を計算できます。
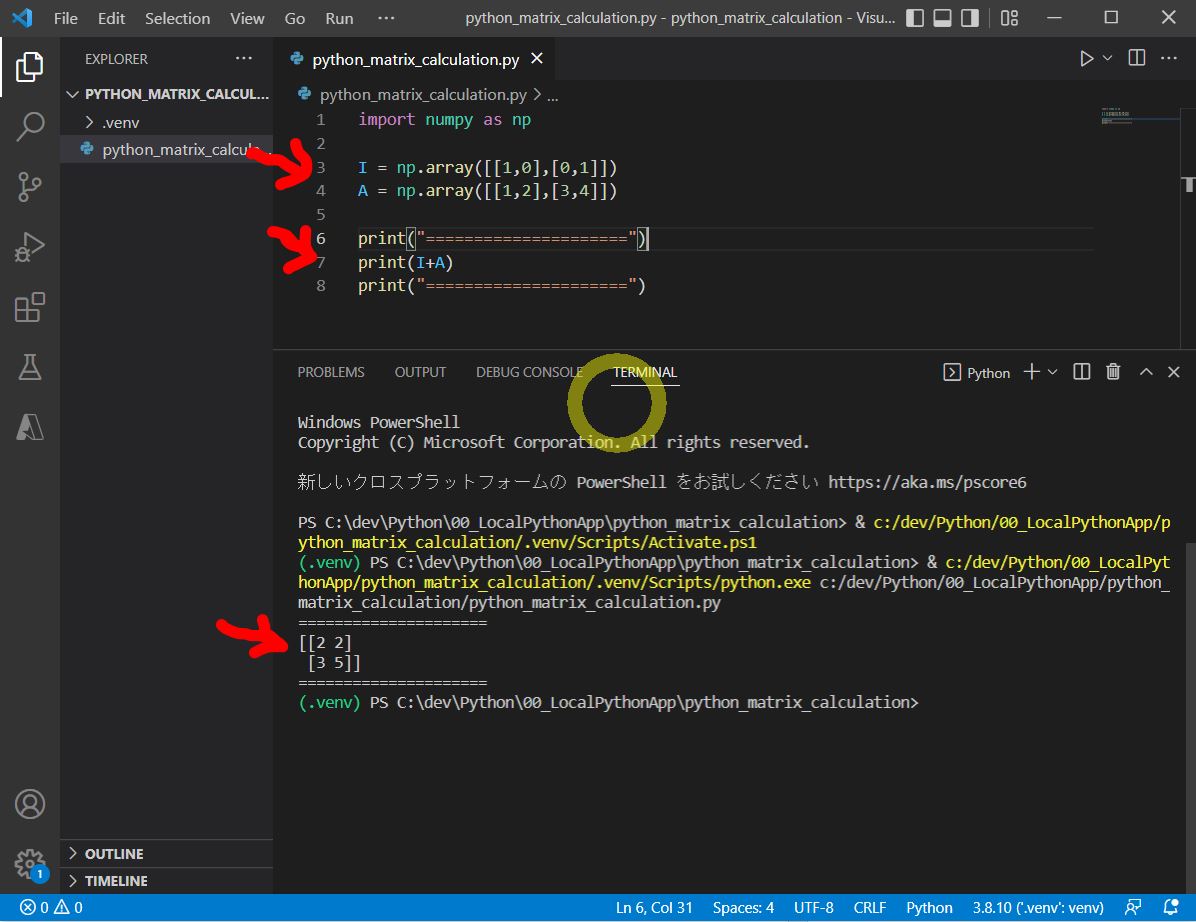
・①「+」:足し算
(例)
I = np.array([[1,0],[0,1]]) A = np.array([[1,2],[3,4]]) print(I+A)
[[2 2] [3 5]]
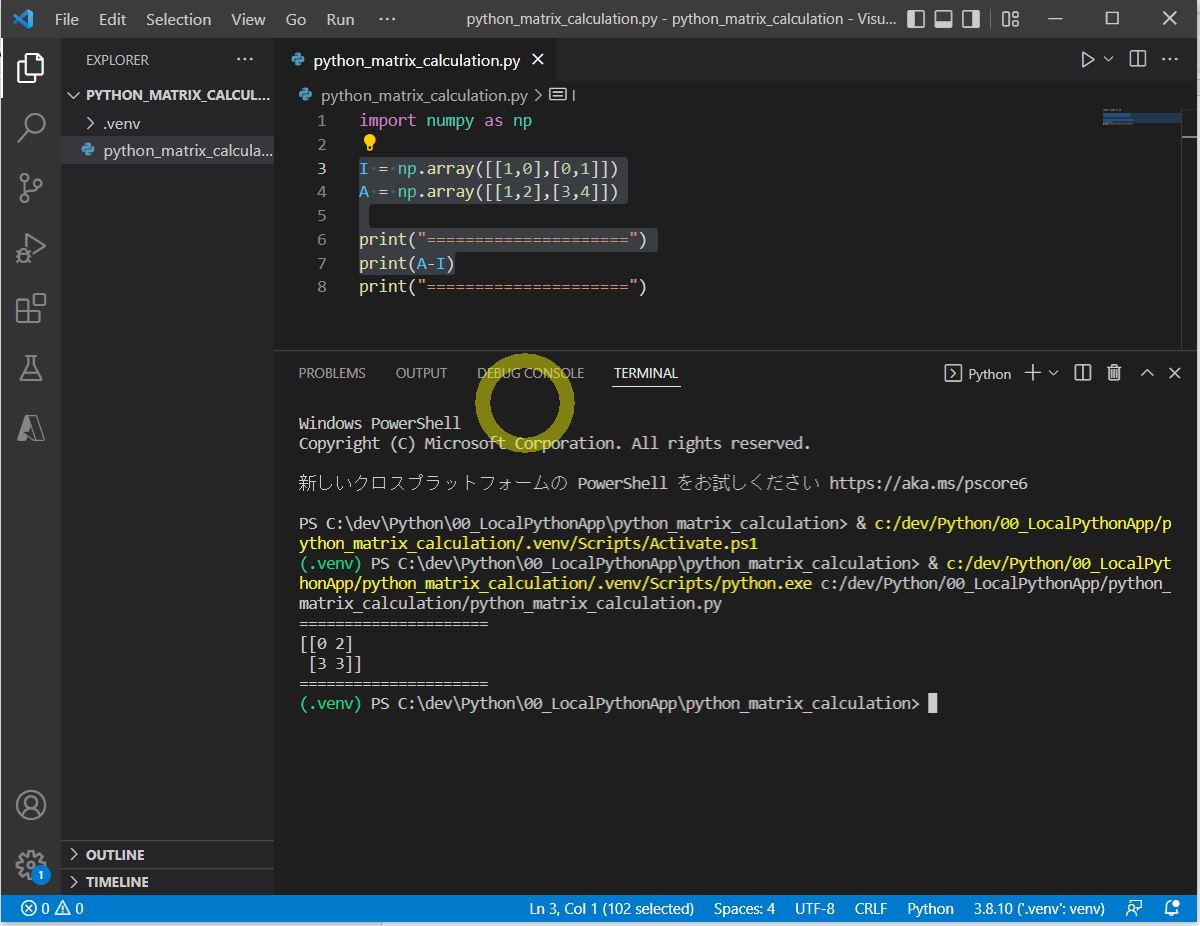
・②「-」:引き算
I = np.array([[1,0],[0,1]]) A = np.array([[1,2],[3,4]]) print(A-I)
[[0 2] [3 3]]
・③「*」:各要素同士の掛け算
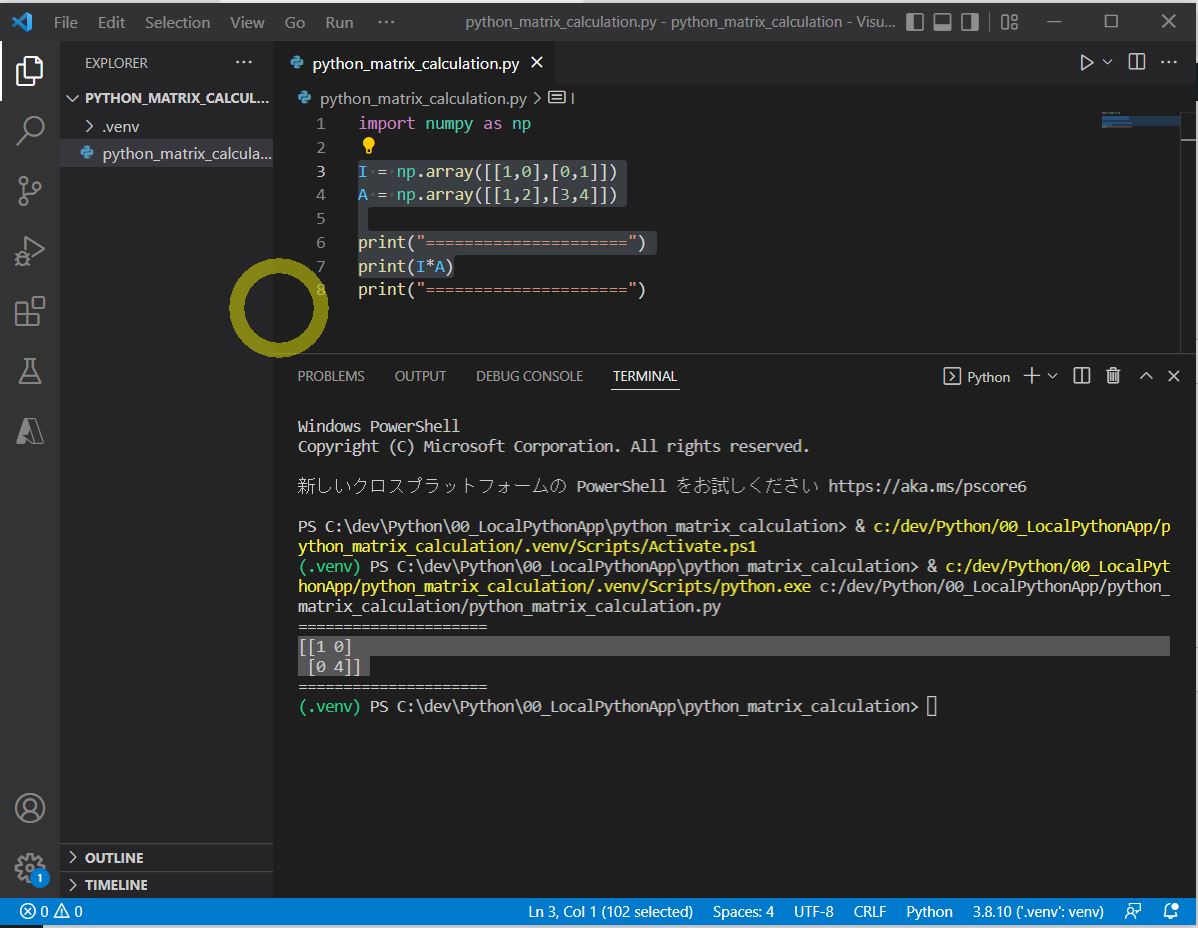
I = np.array([[1,0],[0,1]]) A = np.array([[1,2],[3,4]]) print(I*A)
[[1 0] [0 4]]
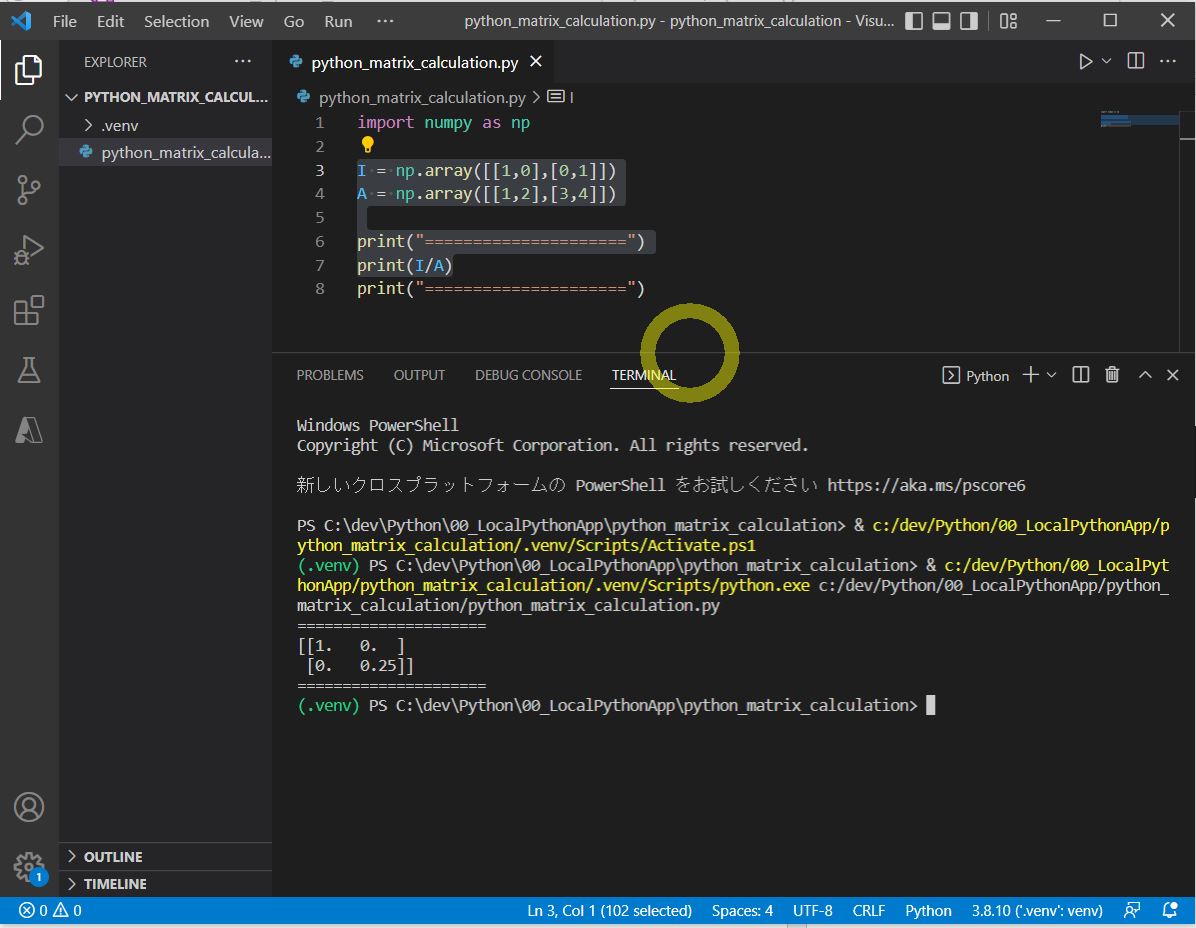
・④「/」:各要素同士の割り算
I = np.array([[1,0],[0,1]]) A = np.array([[1,2],[3,4]]) print(I/A)
[[1. 0. ] [0. 0.25]]
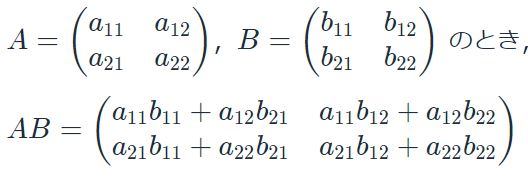
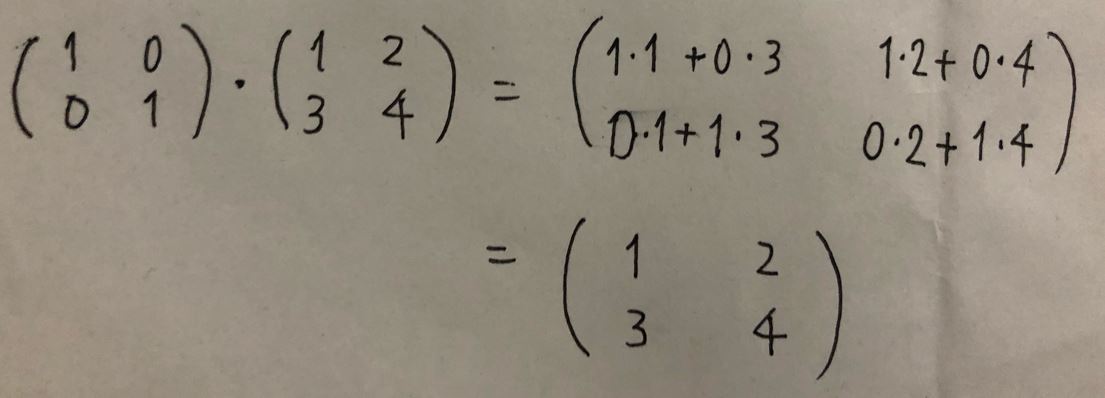
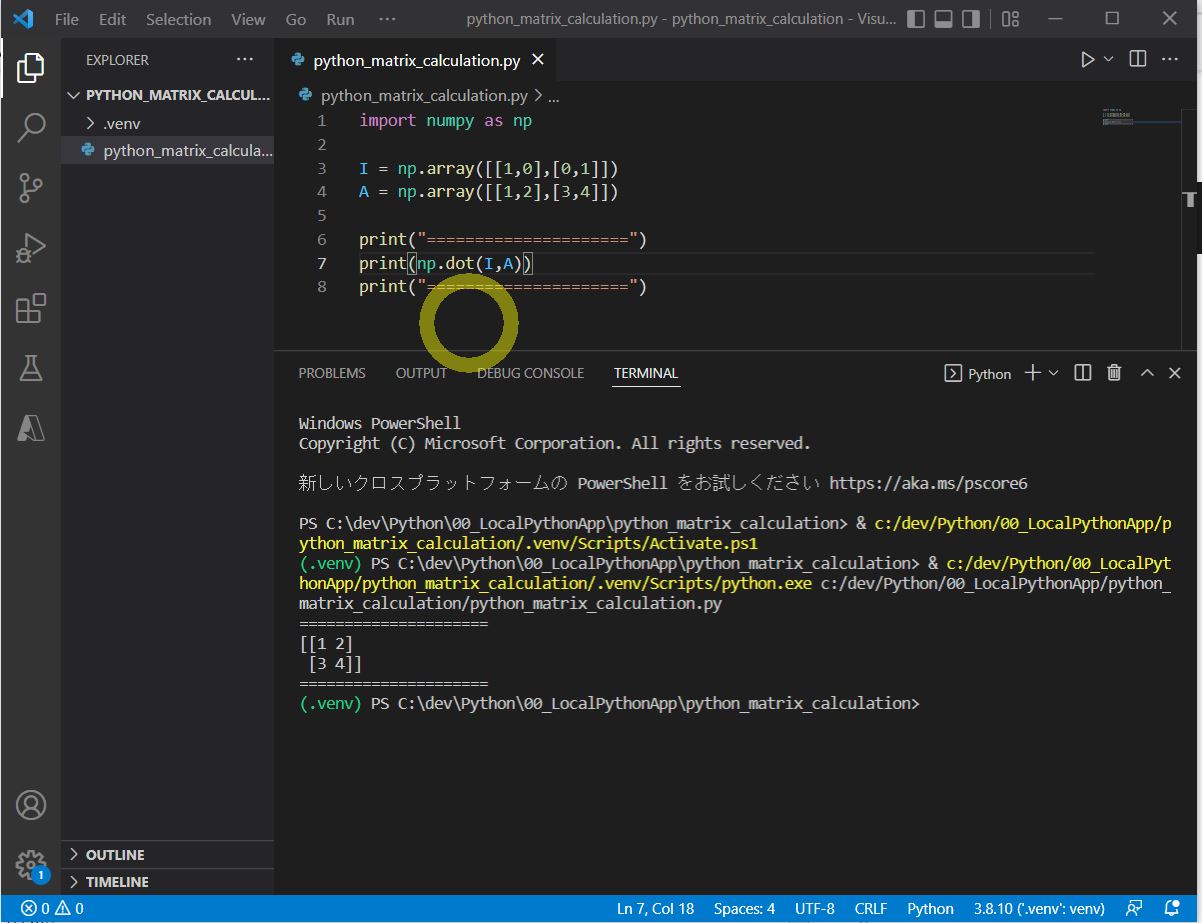
I = np.array([[1,0],[0,1]]) A = np.array([[1,2],[3,4]]) print(np.dot(I,A))
[[1 2] [3 4]]
(1-5) 補足:ベクトルの場合
a = np.array([0,1,0]) b = np.array([1,2,3])
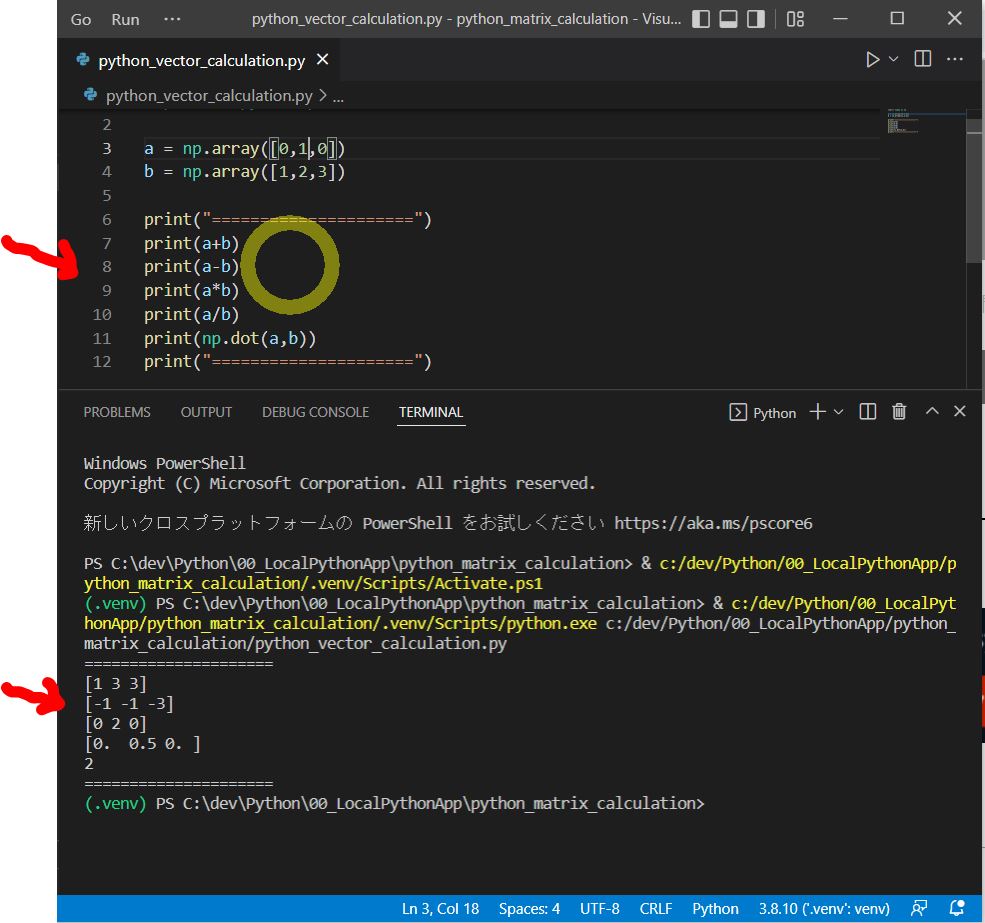
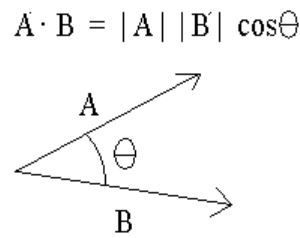
(1-6) 内積とは?